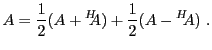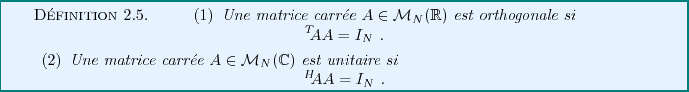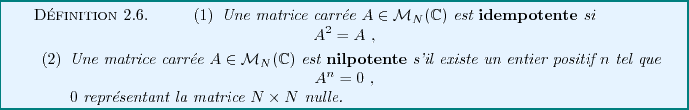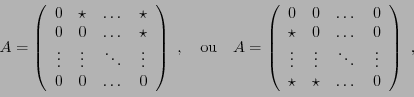Subsections
Calcul Matriciel
Les matrices jouent un rôle fondamental en algèbre linéaire, où
elles fournissent un outil de calcul irremplaçable.
L'objectif de ce chapitre est de donner les premières définitions
et les bases du calcul matriciel, qui seront utilisées dans les
chapitres suivants. On fait également le lien avec les systèmes
linéaires, et la méthode du pivot de Gauss.
On va introduire ici les matrices, comme de nouveaux objets mathématiques,
puis un certain nombre d'opérations sur et avec des matrices. Ceci nous
permettra de voir que certaines matrices, à savoir les matrices carrées,
peuvent être considérées comme une généralisation des
nombres usuels (réels, complexes,...), dans la mesure où on verra
qu'on peut les additionner et les multiplier entre elles. On verra qu'il
existe toutefois quelques différences importantes entre matrices et nombres,
comme par exemple le fait que le produit des matrices carrées n'est pas
commutatif.
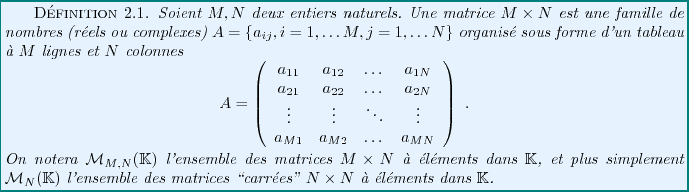
Les cas particuliers les plus couramment rencontrés sont les suivants:
- Matrices carrées:
ce sont des matrices dont le nombre de lignes
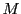 est égal au nombre
est égal au nombre 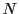 de colonnes. On vera que ces matrices carrées
possèdent un certain nombre de propriétés spécifiques
que n'ont pas les matrices ``rectangulaires'' quelconques.
de colonnes. On vera que ces matrices carrées
possèdent un certain nombre de propriétés spécifiques
que n'ont pas les matrices ``rectangulaires'' quelconques.
- Matrices colonnes
(parfois appelées ``vecteurs colonne''): ce sont
des matrices
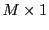
Etant donné un vecteur 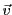 dans un espace vectoriel de dimension
finie
dans un espace vectoriel de dimension
finie 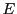 , et une base
, et une base
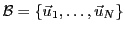 de ce dernier, on
a vu que
de ce dernier, on
a vu que 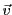 admet une unique décomposition comme combinaison
linéaire sur la base
admet une unique décomposition comme combinaison
linéaire sur la base
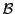 :
:
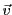 est donc complètement caractérisé par ses coordonnées
dans la base
est donc complètement caractérisé par ses coordonnées
dans la base
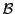 , que l'on a coutume de représenter par une matrice
colonne
, que l'on a coutume de représenter par une matrice
colonne
Il est très important de remarquer que cette matrice colonne dépend
non seulement de 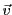 , mais aussi de la base
, mais aussi de la base
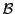 . Si une autre base
. Si une autre base
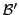 est choisie, les coordonnées changent:
est choisie, les coordonnées changent:
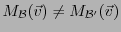 en général.
en général.
- Matrices lignes:
(parfois appelées ``vecteurs ligne'',
ou ``covecteurs''): ce sont des matrices
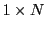 .
.
Une matrice ligne n'est finalement pas autre chose qu'un 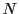 -uplet, on
peut donc identifier l'ensemble
-uplet, on
peut donc identifier l'ensemble
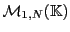 avec
avec
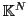 .
.
La matrice identité 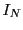 est une matrice
est une matrice
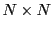 dont tous les éléments sont nuls, sauf les
éléments diagonaux qui valent 1:
dont tous les éléments sont nuls, sauf les
éléments diagonaux qui valent 1:
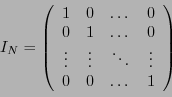 |
(2.1) |
On peut effectuer un certain nombre d'opérations simples sur les matrices.
- Addition des matrices:
Soient
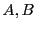 deux matrices
deux matrices 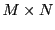 . La matrice
. La matrice 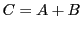 est
la matrice
est
la matrice 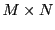 , dont les éléments sont les nombres
, dont les éléments sont les nombres
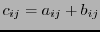 :
:
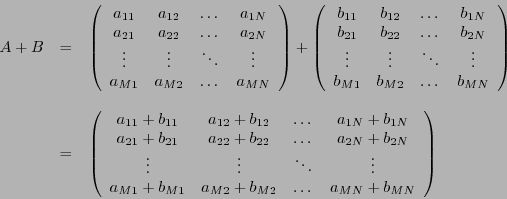 |
(2.2) |
On ne peut additionner que des matrices de même taille
La matrices résultante est de même taille
- Multiplication par un scalaire.
Soit
 une matrice
une matrice 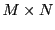 , et soit
, et soit 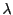 un scalaire
(réel ou complexe). Le produit de
un scalaire
(réel ou complexe). Le produit de 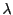 par
par  est la matrice
est la matrice
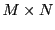 notée
notée 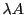 , et définie par
, et définie par
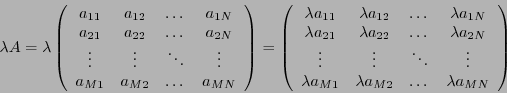 |
(2.3) |
La matrices résultante est de même taille que
la matrice initiale
- Transposition.
Soit
 une matrice
une matrice 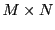 . La transposée de
. La transposée de  , notée
, notée
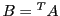 , est la matrice
, est la matrice 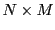 définie par
définie par
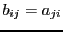 :
:
 |
(2.4) |
Par exemple, la transposée d'une matrice carrée est encore une
matrice carrée de même taille; la transposée d'une matrice
colonne de 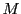 éléments est une matrice ligne de
éléments est une matrice ligne de 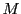 éléments,
et la transposée d'une matrice ligne de
éléments,
et la transposée d'une matrice ligne de 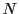 éléments est
une matrice colonne de
éléments est
une matrice colonne de 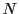 éléments.
éléments.
- Conjugaison Hermitienne.
Soit
 une matrice
une matrice 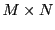 . La conjuguée Hermitienne de
. La conjuguée Hermitienne de  , notée
, notée
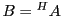 , est la matrice
, est la matrice 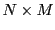 définie par
définie par
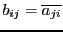 :
:
 |
(2.5) |
La conjuguée Hermitienne d'une matrice carrée est encore une
matrice carrée de même taille; la conjuguée Hermitienne d'une matrice
colonne de 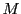 éléments est une matrice ligne de
éléments est une matrice ligne de 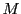 éléments,
et la conjuguée Hermitienne d'une matrice ligne de
éléments,
et la conjuguée Hermitienne d'une matrice ligne de 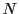 éléments est
une matrice colonne de
éléments est
une matrice colonne de 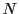 éléments.
éléments.
Par exemple, la transposée de la matrice 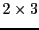
est la matrice
alors que sa conjuguée Hermitienne est la matrice
Une conséquence importante des deux premières propriétés listées
ci-dessus est le théorème suivant:

En effet, les opérations d'addition des matrices et de multiplications des
matrices par un scalaire sont bien définies. On peut aussi facilement
vérifier que tous les axiomes de la définition d'un
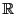 (ou
(ou
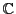 )-espace vectoriel sont bien satisfaits.
)-espace vectoriel sont bien satisfaits.
Sous certaines conditions, les matrices peuvent être multipliées entre
elles, pour donner d'autres matrices. La règle d'or du produit matriciel
est la suivante:
Dans un produit 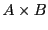 de deux matrices
de deux matrices
 et
et 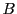 , les lignes de
, les lignes de  sont multipliées élément par élément
par les colonnes de
sont multipliées élément par élément
par les colonnes de 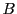 . Il faut donc que les lignes de
. Il faut donc que les lignes de  aient le
même nombre d'éléments que les colonnes de
aient le
même nombre d'éléments que les colonnes de 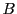 .
.
L'une des opérations fondamentales est le produit d'une matrice par un
vecteur colonne. La règle opératoire est simple.
Soit
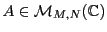 une matrice
une matrice 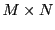 (c'est à dire, à
(c'est à dire, à 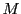 lignes et
lignes et 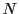 colonnes), et soit
colonnes), et soit
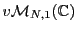 une matrice colonne, à
une matrice colonne, à 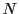 lignes:
lignes:
Alors
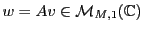 est une matrice colonne, à
est une matrice colonne, à 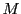 lignes
lignes
Cette opération est bien conforme à la règle d'or
énoncée plus haut: la longueur des lignes de la matrice
(donc, le nombre de colonnes) est égale au nombre d'éléments
(c'est à dire de lignes) de la colonne.
EXEMPLE 2.1 Calculons par exemple
EXEMPLE 2.2 Application: considérons un système linéaire de deux équations
à trois inconnues
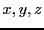
:
On vérifie facilement que ce système peut se mettre sous la forme
d'une égalité entre deux matrices colonne (à deux lignes)
EXEMPLE 2.3 Dans le plan, on peut exprimer l'action d'une rotation
d'angle
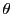
autour de l'origine sur les coordonnées
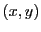
d'un point du plan (voir F
IG. ![[*]](crossref.png)
ci dessous),
sous forme matricielle
Figure:
Rotation d'angle 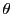 autour de l'origine du plan.
autour de l'origine du plan.
|
|
En effet, en notant
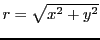 , le point initial peut être
décrit par ses coordonnées polaires
, le point initial peut être
décrit par ses coordonnées polaires
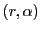 , et
son image par la rotation par ses coordonnées polaires
, et
son image par la rotation par ses coordonnées polaires
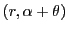 .
On a donc
.
On a donc
ce qui coïncide avec l'égalité ci-dessus.
EXEMPLE 2.4 Dans
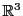
, les rotations autour de l'origine sont plus complexes.
La notion de base reste la notion de rotation dans un plan; par exemple,
la matrice associée à la rotation d'angle
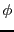
dans le plan
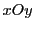
, autour de l'axe
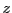
, est de la forme
alors que la matrice de la rotation d'angle
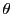
dans le plan
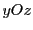
, donc autour de l'axe
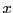
, s'écrit
Figure:
Paramétrisation d'une rotation de
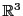 par ses angles d'Euler.
par ses angles d'Euler.
|
|
Il est possible de démontrer que toute matrice de rotation de
l'espace
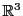 peut se mettre sous la forme d'un produit
de trois matrices
peut se mettre sous la forme d'un produit
de trois matrices
les trois angles
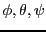
sont appelés
angles d'Euler
de
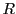
.
EXEMPLE 2.5 En mécanique classique, on repère les coordonnées spatio-temporelles
d'un point par rapport à un référentiel Galiléen par une matrice
colonne
Etant donné un second référentiel Galiléen, en translation
uniforme de vitesse
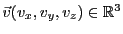
par rapport au premier,
les coordonnées spatio-temporelles du point par rapport au second
référentiel peuvent s'exprimer sous forme matricielle, faisant intervenir
la matrice Galiléenne
On peut en effet écrire les nouvelles coordonnées
L'action de la matrice identité 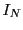 est particulièrement simple:
étant donné une matrice colonne, notée
est particulièrement simple:
étant donné une matrice colonne, notée
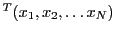 ,
on a
,
on a
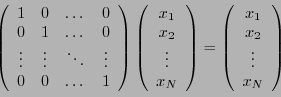 |
(2.6) |
Soient  et
et 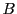 deux matrices carrées
deux matrices carrées 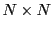 .
Le produit
.
Le produit 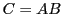 est bien défini, et donne encore une matrice
est bien défini, et donne encore une matrice
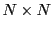
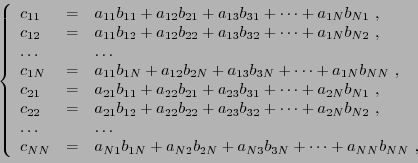 |
(2.7) |
ce que l'on synthétise sous la forme suivante
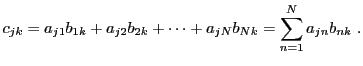 |
(2.8) |
Par exemple, le produit de deux matrices 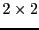 s'écrit
s'écrit
EXEMPLE 2.6 Si l'on reprend le cas des matrices de rotation du plan vue
dans l'exemple
![[*]](crossref.png)
:
on sait que la composée d'une rotation d'angle
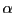
autour de l'origine
par une rotation d'angle
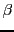
autour de l'origine est toujours
une rotation autour de l'origine du plan, d'angle
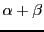
. Au
niveau matriciel, une peu de trigonométrie montre que
EXEMPLE 2.7 Reprenons cette fois l'exemple des matrices Galiléennes
de l'exemple
![[*]](crossref.png)
ci-dessus. Il est clair que
si un premier référentiel est animé d'un mouvement rectiligne de
vitesse
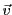
par rapport à un second, lui même animé d'un mouvement
rectiligne de vitesse
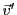
par rapport à un troisième, le premier est
animé d'un mouvement rectiligne de vitesse
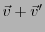
par rapport
au troisième. En termes de matrice, les coordonnées du point considéré
par rapport au troisième référentiel s'expriment sous la forme
ce qui amène à considérer le produit matriciel
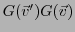
.
On obtient alors facilement
d'où
On peut noter que dans ces deux derniers exemples, le produit de ces matrices
était commutatif. Par exemple,
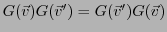 . Il est
important de se souvenir que tel n'est pas toujours le cas, comme le montre
l'exemple suivant: on a
. Il est
important de se souvenir que tel n'est pas toujours le cas, comme le montre
l'exemple suivant: on a
alors que
Donc, le produit matriciel est (en général) non commutatif.
Par contre, quelques calculs permettent de montrer que

REMARQUE 2.1
- Soient
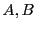 et
et 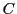 trois matrices carrées. L'égalité
trois matrices carrées. L'égalité
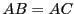 entre les produits de matrices
entre les produits de matrices 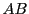 et
et 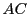 n'implique pas
n'implique pas 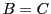 .
.
- Etant données deux matrices carrées
 et
et 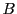 , on peut avoir
, on peut avoir
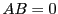 sans que
sans que 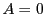 ni
ni 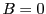 .
.
Là encore, la matrice identité joue un rôle particulier.
On vérifie aisément, en utilisant la définition du produit
des matrices carrées
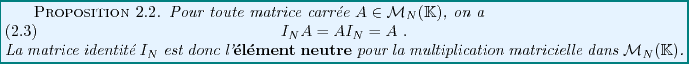
Il est parfois possible de multiplier entre elles des matrices
rectangulaires. Un premier exemple est le produit
``matrice-vecteur'' que nous avons vu plus haut. Le cas des matrices
carrées est lui aussi un exemple particulier.
Dans le cas général, il n'est pas possible de multiplier
n'importe quelle matrice par n'importe quelle matrice. La règle d'or
énoncée plus haut impose des contraintes fortes.
Plus précisément, pour pouvoir multiplier deux matrices
 et
et 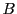 , il faut et il suffit que les lignes de
, il faut et il suffit que les lignes de  aient
même longueur que les colonnes de
aient
même longueur que les colonnes de 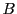 .
Voir en FIG.
.
Voir en FIG. ![[*]](crossref.png) pour une preprésentation
graphique de la situation.
pour une preprésentation
graphique de la situation.
Figure:
Représentation schématique du produit de matrices
rectangulaires
|
|
Ainsi, si
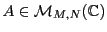 est une matrice
est une matrice 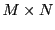 et
si
et
si
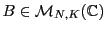 est une matrice
est une matrice 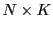 , alors
on pourra effectuer le produit
, alors
on pourra effectuer le produit 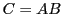 .
. 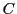 est alors une
matrice
est alors une
matrice 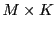 , dont les éléments sont donnés
par
, dont les éléments sont donnés
par
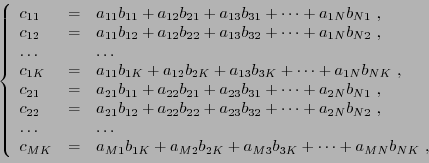 |
(2.9) |
ce que l'on synthétise sous la forme suivante
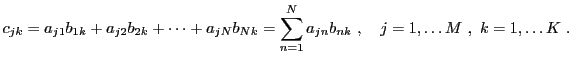 |
(2.10) |
EXEMPLE 2.8 Calculons le produit d'une matrice
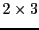
par une matrice
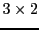
on obtient bien une matrice
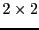
.
La question de la commutativité des matrices rectangulaires ne
se pose pas (à moins qu'elles ne soient carrées). Si  et
et 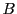 ne
sont pas des matrices carrées, on ne pourra pas calculer à la fois
le produit
ne
sont pas des matrices carrées, on ne pourra pas calculer à la fois
le produit 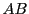 et le produit
et le produit 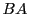 . Par contre, on a
. Par contre, on a

Il est possible de montrer le résultat suivant, donné sans
démonstration ici.
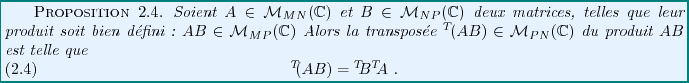
Ainsi, la transposition inverse l'ordre des matrices dans un produit
matriciel.
De façon plus générale, cette propriété reste vraie dans le
cas de produits de plusieurs matrices: étant données une famille
de matrices
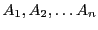 telles que le produit
telles que le produit
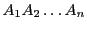 ait un sens, on a
ait un sens, on a
Partant de la définition du produit de matrices carrées, on peut
considérer le cas particulier des puissances d'une matrice.
En effet, étant donnée une matrice
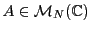 , on
peut considérer les matrices
, on
peut considérer les matrices 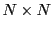 définies par
définies par
et par récurrence la 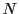 -ième puissance d'une matrice
-ième puissance d'une matrice 
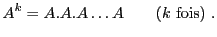 |
(2.11) |
EXEMPLE 2.9 Reprenons le cas des rotations du plan, en posant
et utilisant les calculs précédents, on voit facilement que
et plus généralement, par récurrence
A quoi cela sert-il ? supposons que nous ayions à étudier une
transformation linéaire du plan, associant à un point 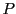 de coordonnées
de coordonnées 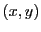 le point
le point 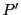 de coordonnées
de coordonnées
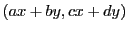 . Organisant les
coordonnées sous forme d'un vecteur colonne, on peut écrire
. Organisant les
coordonnées sous forme d'un vecteur colonne, on peut écrire
avec une matrice
Si on applique une deuxième fois cette transformation, on va aboutir à
un nouveau point du plan dont les coordonnées sont données par
et en appliquant 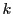 fois cette transformation, on aboutit à
un nouveau point du plan dont les coordonnées sont données par
fois cette transformation, on aboutit à
un nouveau point du plan dont les coordonnées sont données par
On verra à la fin de ce cours des techniques permettant de calculer
simplement des puissances d'une matrice.
On a déjà vu que les matrices carrées possèdent un statut
particulier. En effet, le produit de deux matrices de
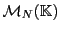 est encore une matrice de
est encore une matrice de
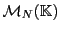 . De plus, on a vu que la matrice
identité
. De plus, on a vu que la matrice
identité 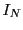 joue un rôle d'élément neutre pour le produit
matriciel dans
joue un rôle d'élément neutre pour le produit
matriciel dans
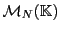 . Il est donc naturel de s'interroger sur
l'existence d'une notion d'inverse d'une matrice.
. Il est donc naturel de s'interroger sur
l'existence d'une notion d'inverse d'une matrice.
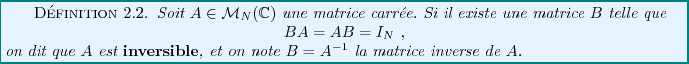
On verra plus loin qu'il est possible de simplifier cette définition, et
de montrer le résultat suivant.

REMARQUE 2.2 On peut considérer que les matrices sont en quelque sorte une
généralisation des nombres, puisque l'on peut les additionner,
les soustraire et les multiplier. La première différence de marque
entre nombres et matrices tient dans le fait que le produit matriciel
n'est pas commutatif en général, contrairement au produit des
nombres. Une seconde différence fondamentale est que toute matrice n'admet
pas nécessairement une matrice inverse (parmi les nombres, seul le
nombre zéro n'admet pas d'inverse). On verra par exemple que des
matrices très simples, telles que
et bien d'autres encore, n'admettent pas d'inverse. C'est ce qui
fait une des difficultés,... mais aussi le piment du calcul matriciel...
Etant donnée une matrice
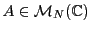 , rechercher l'inverse de
, rechercher l'inverse de
 revient à résoudre (si possible) un système de
revient à résoudre (si possible) un système de
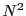 équations à
équations à 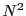 inconnues. Ceci dit, il est possible
de simplifier le problème d'inversion, en exploitant les connexions
avec les systèmes linéaires.
inconnues. Ceci dit, il est possible
de simplifier le problème d'inversion, en exploitant les connexions
avec les systèmes linéaires.
En effet, étant donné une matrice colonne
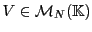 ,
considérons le système linéaire, posé sous forme
matricielle
,
considérons le système linéaire, posé sous forme
matricielle
Síl existe 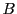 telle que
telle que 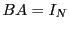 , alors on pourra écrire
, alors on pourra écrire
ou encore
c'est à dire que l'on aura résolu le système linéaire.
Inversement, la solution du système linéaire, si elle existe,
prendra nécessairement cette forme. Par conséquent, inverser  équivaut à résoudre le système linéaire
équivaut à résoudre le système linéaire 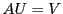 pour
un membre de droite
pour
un membre de droite 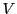 quelconque.
quelconque.
EXEMPLE 2.10 Reprenons l'exemple d'une matrice de rotation
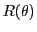
.
Naturellement, la matrice inverse ne pàeut être autre
que
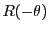
. Vérifions le en résolvant le système
linéaire
autrement dit
qui équivaut à
En reportant la seconde équation dans la première,
on obtient
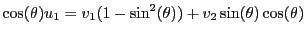
,
d'où la solution sous forme matricielle
et finalement
Considérons deux matrices carrées
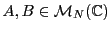 , supposées
inversibles. On peut alors former le produit
, supposées
inversibles. On peut alors former le produit
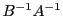 , et calculer
, et calculer
On a donc montré
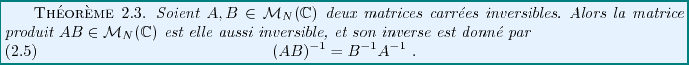
REMARQUE 2.3 On pourrait s'étonner que l'inverse du produit de deux matrices soit
le produit des inverses,
dans l'ordre inverse. En fait, ceci est tout
sauf surprenant, si l'on interprète correctement les choses.
En prenant une analogie dans la vie courante, quelle est l'opération inverse
de l'opération matinale ``mettre ses chaussettes puis mettre ses
chaussures'' ? on ôte tout d'abord ses chaussures, avant d'ôter ses
chaussettes. Il se passe la même chose avec les matrices. Multiplier
par
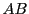
une matrice colonne revient à la multiplier par
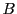
, puis
multiplier le résultat par

. L'opération inverse sera donc de
multiplier par
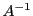
, puis par
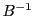
, ce qui revient à multiplier
par
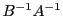
.
Le pivot de Gauss, qu'on a vu précédemment, peut se mettre sous forme
matricielle. En effet, considérons un système linéaire de 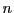 équations à
équations à 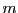 inconnues
inconnues
Ce système linéaire peut se mettre sous forme matricielle
et les manipulations que nous avons effectuées dans le cadre de l'application
de la méthode du pivot peuvent elles aussi s'écrire sous cette forme.
On peut par exemple introduire la notation suivante, en accolant à la matrice
 la colonne de
la colonne de 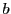 , séparée par une ligne verticale pour éviter
tout risque de confusion avec une matrice:
, séparée par une ligne verticale pour éviter
tout risque de confusion avec une matrice:
Attention ! Il s'agit uniquement d'une notation
destinée à simplifier l'écriture d'un système linéaire. Ceci
n'introduit aucun objet mathématique nouveau.
Reprenant ce que nous avons vu au chapitre précédent, on peut de nouveau
dire que l'ensemble des solutions du système ne change pas lorsque
- On permute l'ordre des lignes
- On multiplie (terme à terme) une ligne par un scalaire non-nul.
- On ajoute à une ligne une combinaison linéaire quelconque
des autres lignes.
EXEMPLE 2.11 Reprenons le système linéaire de trois équations à trois inconnues
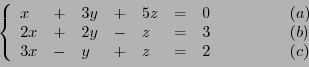 |
(2.12) |
Sous forme matricielle, on peut reformuler ce système via le tableau
que l'on transforme en
puis en forme échelonnée
On obtient donc directement la solution: la dernière ligne nous donne
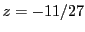
, la deuxième
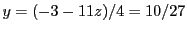
, puis finalement
la première donne
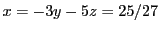
.
Certaines matrices carrées possèdent des propriétés
caractéristiques qui ont d'importantes conséquences.
On en donne une liste non exhaustive ci dessous.
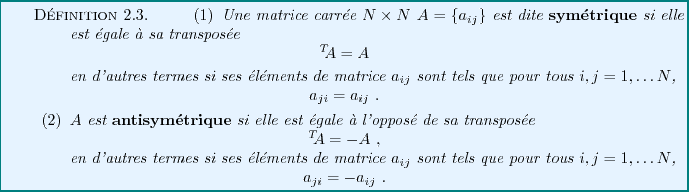
Notons que les éléments diagonaux d'une matrice
antisymétrique sont nécessairement nuls.
On peut facilement démontrer que tout matrice peut s'écrire
comme somme d'une matrice symétrique et d'une matrice antisymétrique.
En effet, étant donnée une matrice  quelconque, il suffit d'écrire
quelconque, il suffit d'écrire
On vérifie facilement que
et
de sorte que
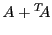 est symétrique, et
est symétrique, et
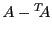 est antisymétrique.
est antisymétrique.
EXEMPLE 2.12 La matrice
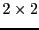
peut sécrire
EXEMPLE 2.13 Dans
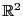
, considérons la matrice
qui agit sur les vecteurs colonne par rotation d'angle
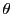
de leurs composantes
Il est immédiat de vérifier que
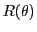
n'est ni symétrique ni
antisymétrique, mais que

Notons par exemple que toute matrice réelle symétrique est Hermitienne,
et que toute matrice réelle antisymétrique est anti-Hermitienne.
Par ailleurs, les éléments diagonaux d'une matrice anti-Hermitienne
sont nécessairement nuls.
Dans le même esprit que ce que nous avons vu
plus haut, tout matrice peut s'écrire
comme somme de'une matrice Hermitienne et d'une matrice anti-Hermitienne.
En effet, étant donnée une matrice  quelconque, il suffit d'écrire
quelconque, il suffit d'écrire
On vérifie facilement que
et
de sorte que
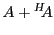 est Hermitienne, et
est Hermitienne, et
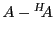 est anti-Hermitienne.
est anti-Hermitienne.
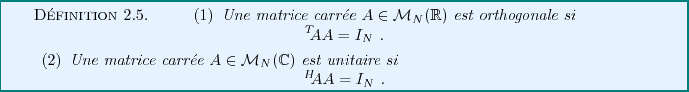
EXEMPLE 2.14 Dans
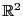
, considérons la matrice de rotation
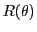
.
On a
et on voit facilement que pour tout
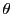
,
donc pour tout
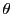
,
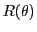
est une matrice orthogonale.
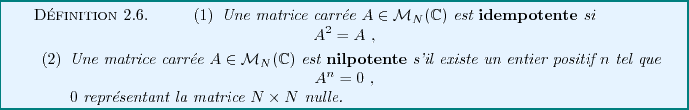
EXEMPLE 2.15 La matrice carrée
est évidemment nilpotente.
Plus généralement, on peut montrer que toute matrice dont tous
les éléments placés au dessus de la diagonale (ou en dessous) sont nuls,
c'est à dire toute matrice de la forme
où
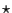
représente un nombre quelconque, est nilpotente.
Bruno Torresani
2009-02-18
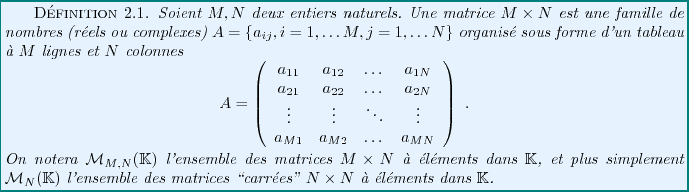
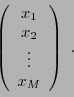
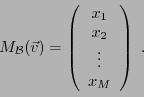
![]() est une matrice
est une matrice
![]() dont tous les éléments sont nuls, sauf les
éléments diagonaux qui valent 1:
dont tous les éléments sont nuls, sauf les
éléments diagonaux qui valent 1:

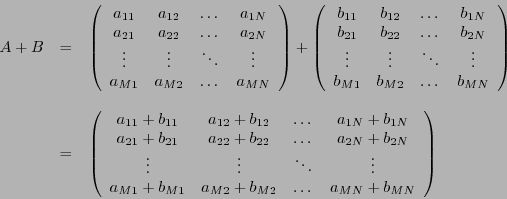
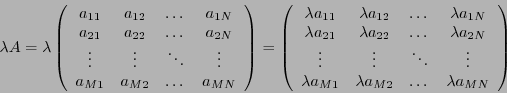


![]()
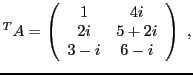
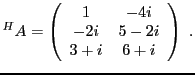

![]() (ou
(ou
![]() )-espace vectoriel sont bien satisfaits.
)-espace vectoriel sont bien satisfaits.
de deux matrices
et
, les lignes de
sont multipliées élément par élément par les colonnes de
. Il faut donc que les lignes de
aient le même nombre d'éléments que les colonnes de
.
![]() une matrice
une matrice ![]() (c'est à dire, à
(c'est à dire, à ![]() lignes et
lignes et ![]() colonnes), et soit
colonnes), et soit
![]() une matrice colonne, à
une matrice colonne, à ![]() lignes:
lignes:

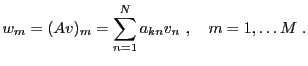
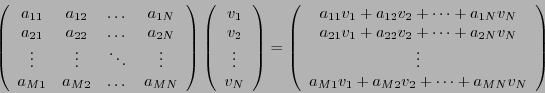
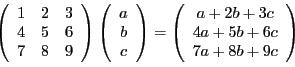
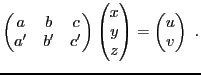
![[*]](crossref.png) ci dessous),
sous forme matricielle
ci dessous),
sous forme matricielle
![]() , le point initial peut être
décrit par ses coordonnées polaires
, le point initial peut être
décrit par ses coordonnées polaires
![]() , et
son image par la rotation par ses coordonnées polaires
, et
son image par la rotation par ses coordonnées polaires
![]() .
On a donc
.
On a donc
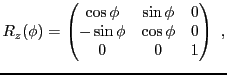
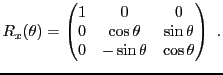
![]() peut se mettre sous la forme d'un produit
de trois matrices
peut se mettre sous la forme d'un produit
de trois matrices
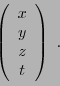
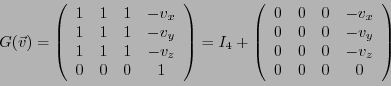
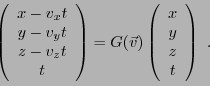
![]() est particulièrement simple:
étant donné une matrice colonne, notée
est particulièrement simple:
étant donné une matrice colonne, notée
![]() ,
on a
,
on a
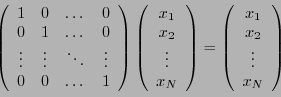
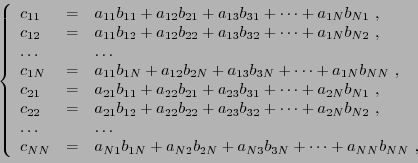
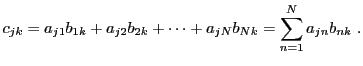
![[*]](crossref.png) :
on sait que la composée d'une rotation d'angle
:
on sait que la composée d'une rotation d'angle ![[*]](crossref.png) ci-dessus. Il est clair que
si un premier référentiel est animé d'un mouvement rectiligne de
vitesse
ci-dessus. Il est clair que
si un premier référentiel est animé d'un mouvement rectiligne de
vitesse 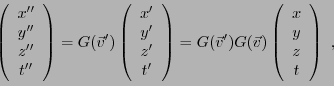


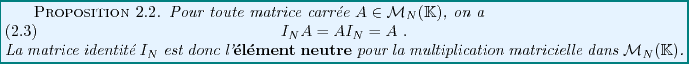
et
, il faut et il suffit que les lignes de
aient même longueur que les colonnes de
. Voir en FIG.
pour une preprésentation graphique de la situation.
![]() est une matrice
est une matrice ![]() et
si
et
si
![]() est une matrice
est une matrice ![]() , alors
on pourra effectuer le produit
, alors
on pourra effectuer le produit ![]() .
. ![]() est alors une
matrice
est alors une
matrice ![]() , dont les éléments sont donnés
par
, dont les éléments sont donnés
par
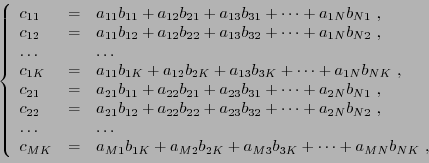
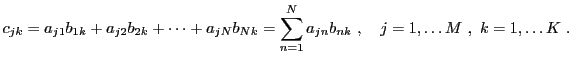
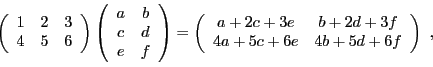
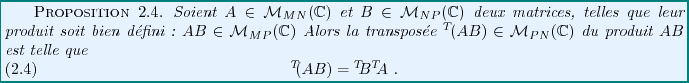
![]() telles que le produit
telles que le produit
![]() ait un sens, on a
ait un sens, on a
![]() de coordonnées
de coordonnées ![]() le point
le point ![]() de coordonnées
de coordonnées
![]() . Organisant les
coordonnées sous forme d'un vecteur colonne, on peut écrire
. Organisant les
coordonnées sous forme d'un vecteur colonne, on peut écrire
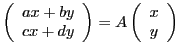
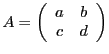
![$\displaystyle A \left[A \left(\begin{array}{c}
x \\ y\end{array}\right)\right]
= A^2 \left(\begin{array}{c}
x \\ y\end{array}\right)
\ ,
$](img532.png)
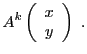
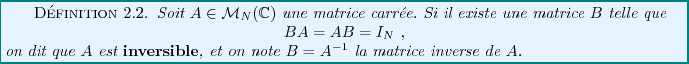
![]()
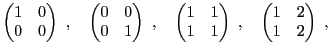
![]() , rechercher l'inverse de
, rechercher l'inverse de
![]() revient à résoudre (si possible) un système de
revient à résoudre (si possible) un système de
![]() équations à
équations à ![]() inconnues. Ceci dit, il est possible
de simplifier le problème d'inversion, en exploitant les connexions
avec les systèmes linéaires.
inconnues. Ceci dit, il est possible
de simplifier le problème d'inversion, en exploitant les connexions
avec les systèmes linéaires.
![]() ,
considérons le système linéaire, posé sous forme
matricielle
,
considérons le système linéaire, posé sous forme
matricielle
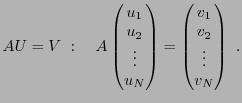
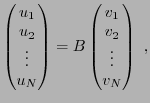
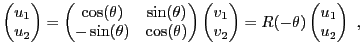
![]() , supposées
inversibles. On peut alors former le produit
, supposées
inversibles. On peut alors former le produit
![]() , et calculer
, et calculer
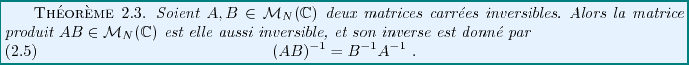
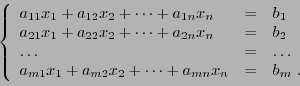
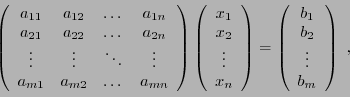
![]() la colonne de
la colonne de ![]() , séparée par une ligne verticale pour éviter
tout risque de confusion avec une matrice:
, séparée par une ligne verticale pour éviter
tout risque de confusion avec une matrice:

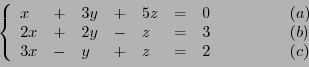
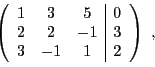
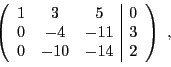
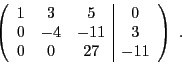
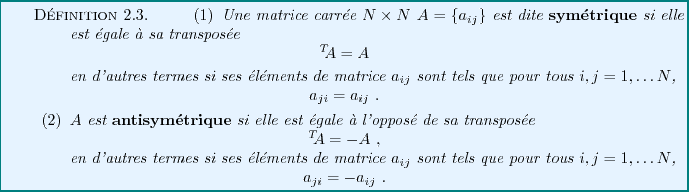
![]() quelconque, il suffit d'écrire
quelconque, il suffit d'écrire
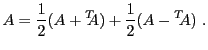
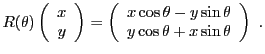

![]() quelconque, il suffit d'écrire
quelconque, il suffit d'écrire