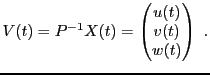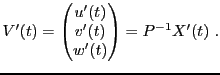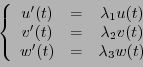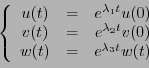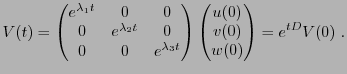Subsections
Diagonalisation des matrices et réduction des endomorphismes
Etant donnés un espace vectoriel  , et un endomorphisme
, et un endomorphisme  de
de  ,
on sait qu'une matrice de
,
on sait qu'une matrice de  dépend de la base de
dépend de la base de  dans laquelle
elle est exprimée. D'où la question: est il possible de trouver une base
particulière de
dans laquelle
elle est exprimée. D'où la question: est il possible de trouver une base
particulière de  dans laquelle la matrice serait la plus simple possible.
Pour illustrer cette problématique, il est utile de considérer quelques
exemples simples.
dans laquelle la matrice serait la plus simple possible.
Pour illustrer cette problématique, il est utile de considérer quelques
exemples simples.
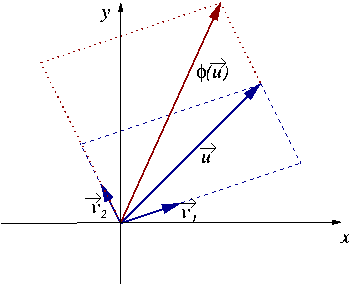
EXEMPLE 5.1 Dans
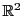
, on considère une application linéaire
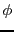
.
Supposons qu'on ait trouvé deux vecteurs
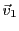
et
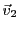
tels que
la famille
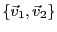
soit libre, et que
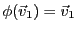
et
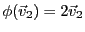
. Alors, la famille étant libre, c'est une
base de
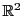
, et tout vecteur
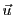
admet une unique décomposition
de la forme
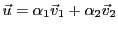
. Par exemple, dans la
figure
![[*]](crossref.png)
, on a
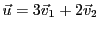
. Alors l'image de
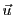
par
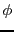
est très facile à calculer.
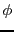
étant
linéaire, on a
.
En l'occurrence, on voit facilement sur la figure
![[*]](crossref.png)
comment est obtenu
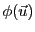
.
Figure:
Construction de l'image d'un vecteur du plan par une application
linéaire 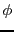 , connaissant deux vecteurs
, connaissant deux vecteurs
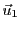 et
et
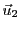 sur lesquels
sur lesquels 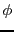 agit par multiplication par un scalaire (ici 1 et 2).
agit par multiplication par un scalaire (ici 1 et 2).
 |
Représenter une application linéaire par une matrice diagonale
peut aussi être très utile pour expliciter des suites de vecteurs,
comme on le voit dans l'exemple ci-dessous, ou résoudre certains
systèmes d'équations différentielles.
EXEMPLE 5.2 Dans
, soit

l'endomorphisme défini par
Sa matrice dans la base canonique
est
On considère maintenant les vecteurs
dont on vérifie facilement qu'ils forment une base de
(puisqu'ils ne sont pas colinéaires), notée
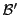
.
Il est clair que
de sorte que la matrice de

dans la base
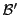
est diagonale
En quoi cela simplifie-t-il les choses ? il suffit de voir que
n'importe quel vecteur du plan
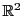
s'écrit de façon unique
et que l'action de

sur cette forme est particulièrement
simple:
EXEMPLE 5.3 Dans
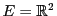
, on considère la suite de vecteurs
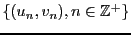
,
définie par
et on cherche à exprimer
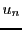
et
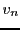
en fonction de
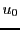
et
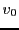
.
Ce problème peut se simplifier par un changement de base approprié.
En notant
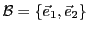
la base canonique, la matrice
du vecteur
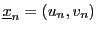
vaut
et on peut donc écrire
On considère une nouvelle base
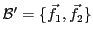
définie par
La matrice de passage prend la forme
et on montre facilement par le calcul que son inverse est donnée par
Dans la nouvelle base, la matrice

devient
Ecrivons maintenant
On peut donc écrire aussi
et finalement montrer par récurrence
Maintenant, remarquons que comme la matrice
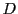
est diagonale,
et que par récurrence, on a aussi
On voit alors que
De là on déduit la solution de notre problème:
Cet exemple nous montre que dès lors que l'on peut trouver une base
dans laquelle un endomorphisme a une matrice diagonale, des calculs
ultérieurs se simplifient considérablement.
Les questions qui se posent maintenant sont essentiellement les
deux questions suivantes:
- Quels sont les endomorphismes qui peuvent être représentés par
une matrice diagonale dans une base bien choisie ?
- Lorsque c'est possible, comment déterminer cette base et la matrice
diagonale ?

Dans ce qui suit, on se focalisera essentiellement sur la diagonalisation
des endomorphismes, si elle est possible.
Considérons un endomorphisme  de
de  , et notons
, et notons  sa matrice par
rapport à une base de référence
sa matrice par
rapport à une base de référence
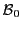 .
Supposons qu'il existe effectivement une base
.
Supposons qu'il existe effectivement une base
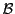 de
de  telle que
la matrice de
telle que
la matrice de  soit diagonalisable, et notons
soit diagonalisable, et notons
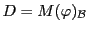 la matrice diagonale correspondante. Notons
la matrice diagonale correspondante. Notons
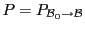 la matrice de passage de la base de référence à la base
la matrice de passage de la base de référence à la base
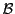 ; on a
donc
; on a
donc
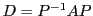 , d'où on tire
, d'où on tire
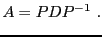 |
(5.1) |
Une importante application de cette propriété est qu'elle
permet de calculer très simplement des puissances d'une matrice.
En effet, supposons que  soit diagonalisable; alors on peut calculer
soit diagonalisable; alors on peut calculer
où la matrice 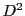 est elle aussi diagonale, de la forme
est elle aussi diagonale, de la forme
Plus généralement, on peut montrer par récurrence

La diagonalisabilité est une notion étroitement liée à la notion
de valeur propre et de vecteur propre.
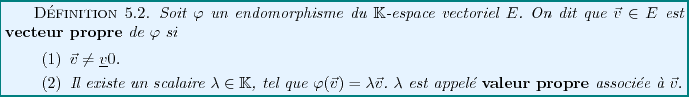
On a alors

Preuve:
Supposons qu'il existe une base
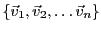 de
de  formée de vecteurs propres, et notons
formée de vecteurs propres, et notons
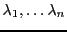 les valeurs propres correspondantes. Alors dans cette base, la matrice
de
les valeurs propres correspondantes. Alors dans cette base, la matrice
de  est automatiquement diagonale.
est automatiquement diagonale.
Inversement, supposons  diagonalisable. Alors il est tout aussi clair
que les vecteurs de base sont des vecteurs propres de
diagonalisable. Alors il est tout aussi clair
que les vecteurs de base sont des vecteurs propres de  .
.
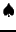
En pratique, on commence tout d'abord par chercher les valeurs propres
de l'endomorphisme considéré (voir l'exemple ci-dessous, ou la
section suivante). On peut ensuite rechercher le ou les vecteur(s)
propre(s) associé(s) à une valeur propre ainsi obtenue 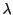 en résolvant l'équation
en résolvant l'équation
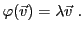
EXEMPLE 5.4 Soit
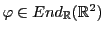
défini par
Chercher des vecteurs propres de

revient à chercher des
couples
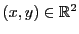
tels que
pour un certain
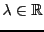
. La première équation nous donne
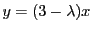
, d'où en reportant dans la seconde on obtient
Si
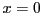
, alors nécessairement
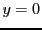
, et
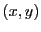
est le vecteur nul,
qui ne peut être vecteur propre par définition. En supposant donc
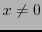
, en simplifiant par
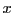
on aboutit à l'équation du second
degré en
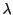
qui donne les valeurs propres possibles:
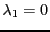
et
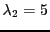
.
Cherchons s'il existe des vecteurs propres associés. Dans le cas de
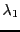 , le vecteur propre associé
, le vecteur propre associé 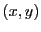 est tel que
est tel que
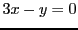 ,
d'où
,
d'où
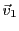 est de la forme
est de la forme
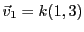 , pour n'importe quel
, pour n'importe quel
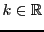 .
Dans le cas de
.
Dans le cas de 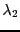 , le vecteur propre associé est tel que
, le vecteur propre associé est tel que
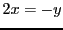 , d'où
, d'où
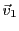 est de la forme
est de la forme
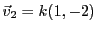 , pour n'importe
quel
, pour n'importe
quel
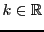 . L'endomorphisme considéré est donc diagonalisable.
. L'endomorphisme considéré est donc diagonalisable.
On a vu dans l'exemple ci-dessus un cas où la recherche de valeurs propres
se ramenait à une recherche de racines d'un polynôme. Cette situation
n'était pas un cas particulier, comme on va le voir.
Soit 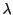 une valeur propre de l'endomorphisme
une valeur propre de l'endomorphisme
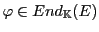 .
Ceci veut dire qu'il existe
.
Ceci veut dire qu'il existe
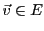 tel que
tel que
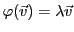 ,
autrement dit
,
autrement dit
Ainsi, l'application linéaire
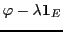 n'est
pas injective, d'où comme on l'a vu au chapitre
n'est
pas injective, d'où comme on l'a vu au chapitre ![[*]](crossref.png)
On rappelle que le déterminant d'un endomorphisme est égal au
déterminant de sa matrice dans une base quelconque (et ne dépend
pas du choix de la base).
Notons
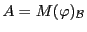 la matrice de
la matrice de  dans une base donnée:
dans une base donnée:
Alors
et l'équation
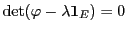 se ramène à une
équation de degré
se ramène à une
équation de degré  en
en 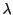 :
:
les 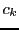 étant des scalaires. Cette équation est appelée
équation caractéristique, et son membre de gauche est le
polynôme caractéristique, noté
étant des scalaires. Cette équation est appelée
équation caractéristique, et son membre de gauche est le
polynôme caractéristique, noté
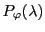 .
.
On a donc montré le résultat

EXEMPLE 5.5 Reprenons l'exemple
![[*]](crossref.png)
ci dessus. La matrice de

est
et l'équation caractéristique prend la forme
ce qui revient à
ce qui est précisément l'équation que nous avions obtenue.
.
Soit
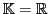 ou
ou
 . On note
. On note
![$ \mathbb{K}[X]$](img1158.png) l'ensemble des polynômes
d'indéterminée
l'ensemble des polynômes
d'indéterminée 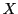 . On rappelle que
. On rappelle que
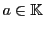 est une racine
du polynôme
est une racine
du polynôme
![$ P\in \mathbb{K}[X]$](img1160.png) si
si 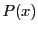 peut s'écrire sous la forme
peut s'écrire sous la forme
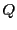 étant un autre polynôme de
étant un autre polynôme de
![$ \mathbb{K}[X]$](img1158.png) .
.
![\begin{definition}
Soit $P\in \mathbb{K}[X]$\ un polyn\^ome de degr\'e $n$. On d...
...ment
distinctes) dans $\mathbb{K}$.
\index{Polyn\^ome scind\'e}
\end{definition}](img1164.png)
Il est possible de démontrer que dans ce cas, le polynôme 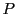 peut être
complètement factorisé, et se mettre sous la forme
peut être
complètement factorisé, et se mettre sous la forme
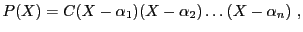 |
(5.2) |
où
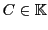 est une constante, et où
est une constante, et où
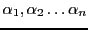 sont les racines de
sont les racines de 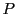 .
Comme on l'a vu, les racines ne sont pas nécessairement distinctes.
En notant
.
Comme on l'a vu, les racines ne sont pas nécessairement distinctes.
En notant
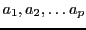 les
les 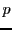 racines distinctes de
racines distinctes de 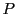 , on
introduit leur multiplicité
, on
introduit leur multiplicité
qui est le nombre d'occurrences de 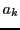 parmi les racines
parmi les racines
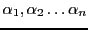 . On a alors
. On a alors
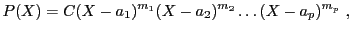 |
(5.3) |
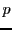 étant donc le nombre de racines distinctes. En identifiant
ces deux expressions, on montre également que
étant donc le nombre de racines distinctes. En identifiant
ces deux expressions, on montre également que
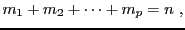 |
(5.4) |
 étant le degré du polynôme
étant le degré du polynôme 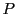 .
.
Tout polynôme n'est pas nécessairement scindé dans
 . Par exemple,
le polynôme
. Par exemple,
le polynôme
n'est pas scindé dans
 . Par contre, il l'est dans
. Par contre, il l'est dans
 , car il admet
deux racines de partie imaginaire non nulle
, car il admet
deux racines de partie imaginaire non nulle
Plus généralement, on sait bien que pour un polynôme de degré deux
celui-ci sera scindé sur
 si son discriminant
si son discriminant
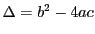 est
positif ou nul, et sera toujours scindé sur
est
positif ou nul, et sera toujours scindé sur
 . Cette dernière
propriété se généralise en fait à des polyhnômes
de degré quelconque:
. Cette dernière
propriété se généralise en fait à des polyhnômes
de degré quelconque:
![\begin{theorem}[Th\'eor\\lq eme de D'Alembert]
Tout polyn\^ome de $\mathbb{C}[X]$\ est scind\'e sur $\mathbb{C}$.
\end{theorem}](img1176.png)
Pour qu'un endomorphisme soit diagonalisable, il faut donc
nécessairement que son polynôme caractéristique soit scindé.
Malheureusement, cette condition n'est pas suffisante, et il faut donc
préciser davantage les choses.
La caractérisation des endomorphismes diagonalisables repose
sur la notion de sous-espace propre.


Preuve: Il est clair que si
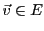 est tel que
est tel que
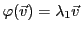 et
et
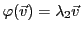 , avec
, avec
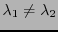 , on a nécessairement
, on a nécessairement
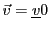 .
.
Ce résultat, conjuqué à la définition d'un endomorphisme
diagonalisable, a une conséquence immédiate

La dernière question en suspens concerne le lien entre les valeurs
propres et les sous-espaces propres.

Dans le cas particulier où toutes les racines sont des racines
simples, on a directement

On considère ci-dessous une série d'endomorphismes de
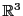 (ou
(ou
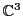 ) définis par leurs matrices, qui donnent un
éventail des situations possibles.
) définis par leurs matrices, qui donnent un
éventail des situations possibles.
EXEMPLE 5.6
Le polynôme caractéristique de

prend la forme
On a trois valeurs propres distinctes, l'endomorphisme considéré
est donc diagonalisable. Cherchons maintenant les vecteurs propres
correspondants. Pour cela, calculons tout d'abord
Les composantes
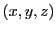
d'un vecteur propre
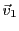
associé
à la valeur propre
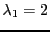
doivent donc satisfaire le système
c'est à dire le système homogène
dont toutes les solutions satisfont
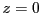
et
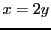
. Par conséquent,
on peut choisir
Cherchons maintenant un vecteur propre
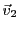
associé à la
valeur propre
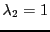
.
Ses composantes
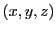
doivent donc satisfaire le système
c'est à dire le système homogène
dont toutes les solutions satisfont
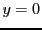
et

. Par conséquent,
on peut choisir
Finalement, les composantes du vecteur propre
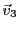
associé à
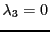
satisfont le système homogène
dont les solutions sont de la forme
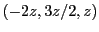
, de sorte qu'un
vecteur propre est
La matrice de passage de la base canonique à la base des vecteurs propres
prend la forme
EXEMPLE 5.7 On considère l'endomorphisme dont la matrice dans la base canonique est
Son polynôme caractéristique vaut
On a cette fois une racine double
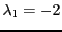
et une racine simple
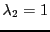
. Pour voir si

est diagonalisable, il faut étudier
le sous-espace propre
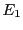
. Soit donc
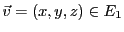
. On a alors
le système
c'est à dire le système homogène
qui équivaut à la seule équation
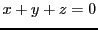
. L'ensemble des solutions
est un espace vectoriel de dimension deux, dont on peut prendre comme base
Donc

est diagonalisable. Pour terminer, on peut aussi trouver un vecteur
propre associé à
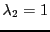
, en résolvant le système
c'est à dire le système homogène
qui équivaut à
dont les solutions satisfont
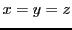
. On peut donc prendre comme vecteur
propre
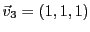
, et écrire
avec
EXEMPLE 5.8 On considère l'endomorphisme dont la matrice dans la base canonique est
Le polynôme caractéristique est donné par
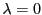
est racine évidente. Pour connaitre les autres racines,
il faut factoriser le polynôme
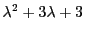
. Son discriminant
vaut
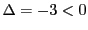
, dont les deux racines sont des nombres complexes
conjugués l'un de l'autre. Par conséquent,
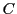
n'est pas

-diagonalisable,
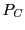
n'étant pas

-scindé.
Par contre,
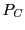
est

-scindé, et admet 3 racines (complexes)
distinctes. Donc,
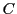
est

-diagonalisable, et on pourra
donc lui associer une base de vecteurs propres. Les valeurs propres
sont complexes, de partie imaginaire non-nulle.
EXEMPLE 5.9 On considère l'endomorphisme dont la matrice dans la base canonique est
Le polynôme caractéristique est (en développant le
déterminant par rapport à la seconde ligne)
Là encore, on a une racine double
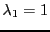
. Etudions le
sous-espace propre associé. Soit
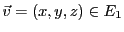
, il doit
satisfaire le système
c'est à dire le système homogène
dont les solutions sont de la forme
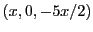
. L'ensemble des solutions
est donc un espace vectoriel de dimension 1, alors que la multiplicité
de
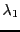
vaut 2. Donc,

n'est pas diagonalisable.
Jusqu'à présent, nous n'avons exploité que la structure d'espace
vectoriel de
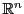 . Or on sait que
. Or on sait que
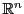 est aussi muni d'autres
types d'opérations, telles que la norme et le produit scalaire.
est aussi muni d'autres
types d'opérations, telles que la norme et le produit scalaire.
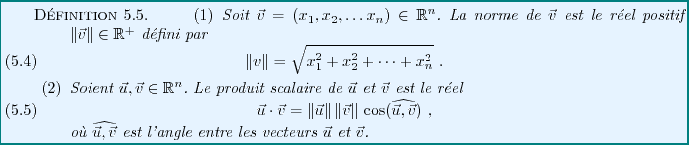
On vérifie facilement que si
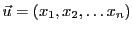 et
et
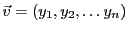 , alors
, alors
Sans entrer dans les détails de la démonstration, qui va au delà des
objectifs de ce cours, il est quand même utile de donner le
résultat suivant, qui donne un critère simple poir la diagonalisabilité
des matrices réelles.

Par conséquent, lorsque l'on est en présence d'une matrice réelle
symétrique
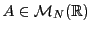 , on est assuré de pouvoir trouver
une base de vecteurs propres
, on est assuré de pouvoir trouver
une base de vecteurs propres
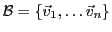 qui est orthonormée, c'est à dire telle que
qui est orthonormée, c'est à dire telle que
Dans le cas complexe, le résultat précédent ne s'applique pas.
Cependant, il peut être généralisé, en introduisant une structure
généralisant celle d'espace Euclidien.
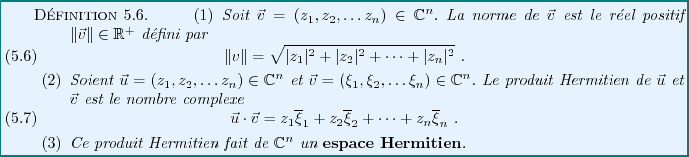
Ceci nous permet d'étendre au cas complexe le théorème
précédent. La condition qui remplace la condition de symétrie de
la matrice est cette fois une condition d'Hermiticité:

La réduction des endomorphismes et la diagonalisation des matrices
permettent de simplifier considérablement un certain nombre de
calculs, comme par exemple le calcul de puissances d'une matrice,
ou la résolution de systèmes différentiels linéaires.
Sans entrer dans les détails, on peut
en donner quelques exemples ici. Avant d'entrer dans le vif du sujet,
il est intéressant de souligner l'aspect le plus important
des calculs que nous allons faire. Dans tous les cas, la diagonalisation
de la matrice considérée va nous permettre de transformer un
problème matriciel, donc compliqué, en un problème dans lequel
les variables sont découplées, ce qui nous ramènera à des
problèmes faisant intervenir des nombres et non plus des matrices.
Par exemple, le calcul des puissances d'une matrice devient très simple
dès lors que l'on a diagonalisé la matrice: la puissance
 -ième d'une matrice diagonale s'obtient en élevant tous ses
éléments de matrice à la puissance
-ième d'une matrice diagonale s'obtient en élevant tous ses
éléments de matrice à la puissance  , ce qui est faux pour des
matrices non diagonales.
, ce qui est faux pour des
matrices non diagonales.
Soit
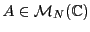 une matrice Hermitienne (ce résultat s'applique
tout aussi bien aux matrices réelles symétriques). Nous avons vu
que
une matrice Hermitienne (ce résultat s'applique
tout aussi bien aux matrices réelles symétriques). Nous avons vu
que  est nécessairement diagonalisable: en notant
est nécessairement diagonalisable: en notant 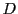 la matrice
diagonale des valeurs propres de
la matrice
diagonale des valeurs propres de  , et
, et 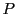 la matrice de passage
correspondante, on a donc
la matrice de passage
correspondante, on a donc
Pour calculer le carré de  , on calcule donc
, on calcule donc
car le carré d'une matrice diagonale est toujours une matrice diagonale,
dont les éléments diagonaux sont les carrés des éléments
diagonaux de la matrice de départ.
Plus généralement, on montre que pour tout entier positif 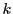 ,
,
Exponentielle d'une matrice
L'exponentielle d'une matrice  est définie par
la série entière
est définie par
la série entière
et on peut donc lui appliquer le résultat précédent si  est
Hermitienne:
est
Hermitienne:
expression calculable si on sait calculer l'exponentielle
d'une matrice diagonale.
On peut en fait facilement voir que 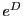 prend une forme simple
prend une forme simple
Ainsi, l'exponentielle d'une matrice diagonale est la matrice diagonale
dont les éléments diagonaux sont les exponentielles des éléments
diagonaux de la matrice de départ.
Ces calculs peuvent se généraliser à d'autres fonctions
que des exponentielles. Par exemple, soit 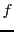 une fonction
à valeurs réelles, telle que
une fonction
à valeurs réelles, telle que 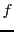 admette un développement
en série entière convergent en 0 (cette hypothèse est très importante):
admette un développement
en série entière convergent en 0 (cette hypothèse est très importante):
Alors, en utilisant les mêmes arguments que ci-dessus, il
va être possible de définir 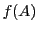 pour une matrice Hermitienne
pour une matrice Hermitienne
 , par
, par
ce qui donne
Pour simplifier, on va ici considérer le cas 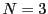 .
.
On considère des instants discrets
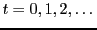 et on suppose que les mouvements d'un point dans l'espace
tridimensionnel, repéré par le vecteur
et on suppose que les mouvements d'un point dans l'espace
tridimensionnel, repéré par le vecteur
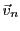 ,
évoluent suivant une suite de la forme
,
évoluent suivant une suite de la forme
où  est une matrice réelle symétrique, donc diagonalisable.
On peut donc écrire encore une fois
est une matrice réelle symétrique, donc diagonalisable.
On peut donc écrire encore une fois
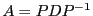 , où
, où
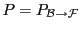 est la matrice de passage
de la base canonique
est la matrice de passage
de la base canonique
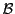 à la base qui diagonalise
à la base qui diagonalise  , que
l'on note
, que
l'on note
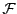 , et où
, et où
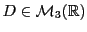 est la matrice
diagonale des valeurs propres de
est la matrice
diagonale des valeurs propres de  , notées
, notées
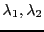 et
et 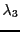 .
.
Notons
la matrice de
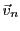 dans la base
dans la base
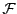 .
On voit facilement que
.
On voit facilement que
On en déduit donc la solution, c'est à dire l'expression de
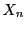 en fonction de la condition initiale
en fonction de la condition initiale 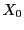 :
:
Le même type de raisonnement s'applique également à la résolution
de systèmes d'équations différentielles linéaires du premier
ordre couplées. Là encore, on va se limiter au cas de systèmes
de trois équations, le cas général se traitant de façon identique.
On considère les positions
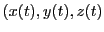 d'un point matériel,
représentées sous forme matricielle par
d'un point matériel,
représentées sous forme matricielle par
et on suppose qu'elles sont décrites par un système d'équations
différentielles, que l'on écrit sous forme matricielle, en posant
où  est une matrice réelle symétrique, donc diagonalisable.
est une matrice réelle symétrique, donc diagonalisable.
En diagonalisant la matrice  comme ci-dessus, on aboutit au système
matriciel
comme ci-dessus, on aboutit au système
matriciel
d'où on déduit
Posons
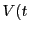 est la matrice colonne des coordonnées de
est la matrice colonne des coordonnées de 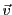 dans la base
qui diagonalise la matrice
dans la base
qui diagonalise la matrice  . De plus, on voit facilement que
. De plus, on voit facilement que
Ainsi, on aboutit à un nouveau système
autrement dit
dont les solutions sont
Sout forme matricielle, on a donc
On en déduit la solution du système
Bruno Torresani
2009-02-18
![]() , et un endomorphisme
, et un endomorphisme ![]() de
de ![]() ,
on sait qu'une matrice de
,
on sait qu'une matrice de ![]() dépend de la base de
dépend de la base de ![]() dans laquelle
elle est exprimée. D'où la question: est il possible de trouver une base
particulière de
dans laquelle
elle est exprimée. D'où la question: est il possible de trouver une base
particulière de ![]() dans laquelle la matrice serait la plus simple possible.
Pour illustrer cette problématique, il est utile de considérer quelques
exemples simples.
dans laquelle la matrice serait la plus simple possible.
Pour illustrer cette problématique, il est utile de considérer quelques
exemples simples.
![[*]](crossref.png) , on a
, on a
![[*]](crossref.png) comment est obtenu
comment est obtenu
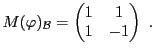
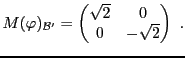
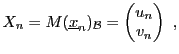
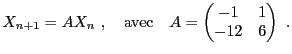
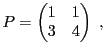
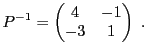
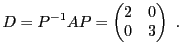
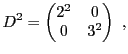
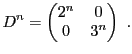
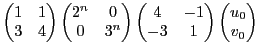
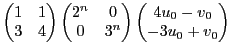
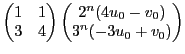
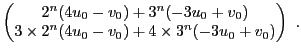

![]() de
de ![]() , et notons
, et notons ![]() sa matrice par
rapport à une base de référence
sa matrice par
rapport à une base de référence
![]() .
Supposons qu'il existe effectivement une base
.
Supposons qu'il existe effectivement une base
![]() de
de ![]() telle que
la matrice de
telle que
la matrice de ![]() soit diagonalisable, et notons
soit diagonalisable, et notons
![]() la matrice diagonale correspondante. Notons
la matrice diagonale correspondante. Notons
![]() la matrice de passage de la base de référence à la base
la matrice de passage de la base de référence à la base
![]() ; on a
donc
; on a
donc
![]() , d'où on tire
, d'où on tire
![]() soit diagonalisable; alors on peut calculer
soit diagonalisable; alors on peut calculer


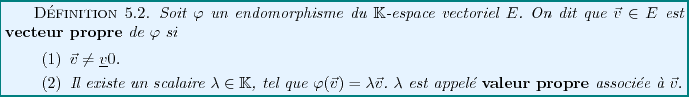
![]()
![]() de
de ![]() formée de vecteurs propres, et notons
formée de vecteurs propres, et notons
![]() les valeurs propres correspondantes. Alors dans cette base, la matrice
de
les valeurs propres correspondantes. Alors dans cette base, la matrice
de ![]() est automatiquement diagonale.
est automatiquement diagonale.
![]() diagonalisable. Alors il est tout aussi clair
que les vecteurs de base sont des vecteurs propres de
diagonalisable. Alors il est tout aussi clair
que les vecteurs de base sont des vecteurs propres de ![]() .
.
![]()
![]() en résolvant l'équation
en résolvant l'équation
![]() , le vecteur propre associé
, le vecteur propre associé ![]() est tel que
est tel que
![]() ,
d'où
,
d'où
![]() est de la forme
est de la forme
![]() , pour n'importe quel
, pour n'importe quel
![]() .
Dans le cas de
.
Dans le cas de ![]() , le vecteur propre associé est tel que
, le vecteur propre associé est tel que
![]() , d'où
, d'où
![]() est de la forme
est de la forme
![]() , pour n'importe
quel
, pour n'importe
quel
![]() . L'endomorphisme considéré est donc diagonalisable.
. L'endomorphisme considéré est donc diagonalisable.![]() une valeur propre de l'endomorphisme
une valeur propre de l'endomorphisme
![]() .
Ceci veut dire qu'il existe
.
Ceci veut dire qu'il existe
![]() tel que
tel que
![]() ,
autrement dit
,
autrement dit
![[*]](crossref.png)
![]() la matrice de
la matrice de ![]() dans une base donnée:
dans une base donnée:

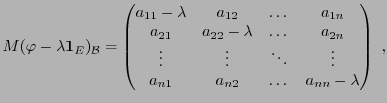

![[*]](crossref.png) ci dessus. La matrice de
ci dessus. La matrice de 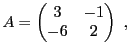
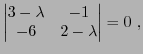
![]() ou
ou
![]() . On note
. On note
![]() l'ensemble des polynômes
d'indéterminée
l'ensemble des polynômes
d'indéterminée ![]() . On rappelle que
. On rappelle que
![]() est une racine
du polynôme
est une racine
du polynôme
![]() si
si ![]() peut s'écrire sous la forme
peut s'écrire sous la forme
![]() . Par exemple,
le polynôme
. Par exemple,
le polynôme
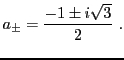
![]()

![]()
![]() est tel que
est tel que
![]() et
et
![]() , avec
, avec
![]() , on a nécessairement
, on a nécessairement
![]() .
.
![]()


![]()
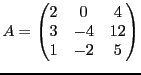
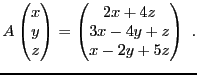
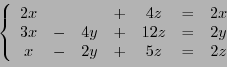
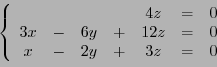
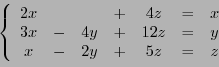
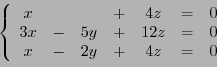
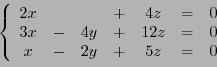
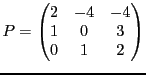
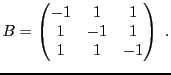
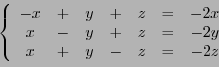
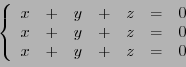
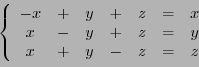
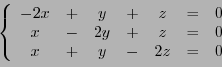
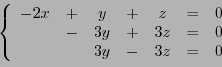
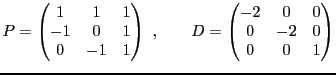
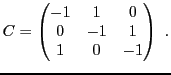
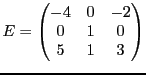
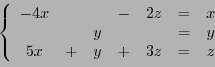
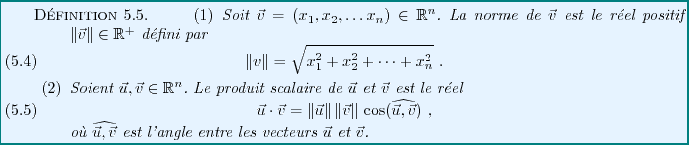

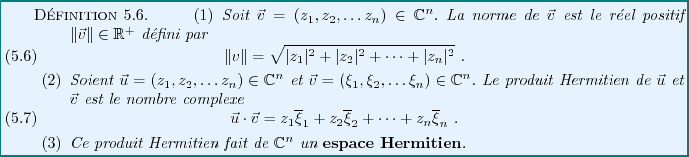

![]() -ième d'une matrice diagonale s'obtient en élevant tous ses
éléments de matrice à la puissance
-ième d'une matrice diagonale s'obtient en élevant tous ses
éléments de matrice à la puissance ![]() , ce qui est faux pour des
matrices non diagonales.
, ce qui est faux pour des
matrices non diagonales.
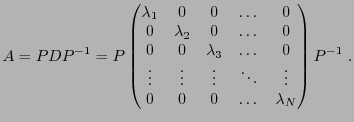
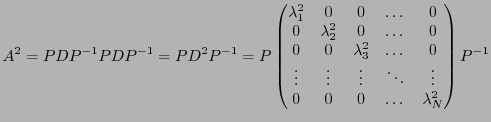
![]() ,
,
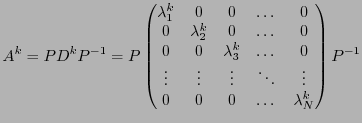
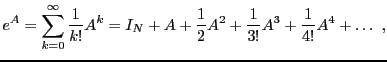
![]() prend une forme simple
prend une forme simple
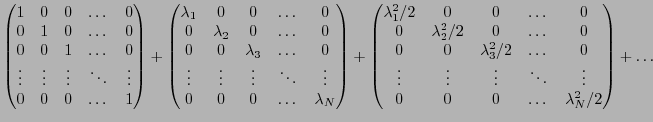
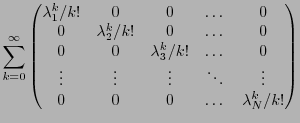
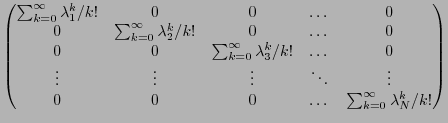

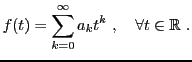
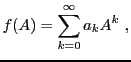
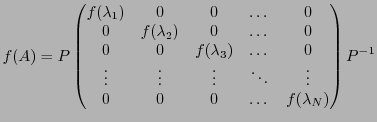
![]() et on suppose que les mouvements d'un point dans l'espace
tridimensionnel, repéré par le vecteur
et on suppose que les mouvements d'un point dans l'espace
tridimensionnel, repéré par le vecteur
![]() ,
évoluent suivant une suite de la forme
,
évoluent suivant une suite de la forme
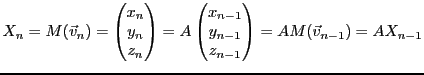
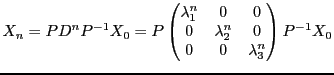
![]() d'un point matériel,
représentées sous forme matricielle par
d'un point matériel,
représentées sous forme matricielle par
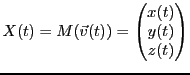
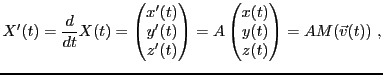
![]() comme ci-dessus, on aboutit au système
matriciel
comme ci-dessus, on aboutit au système
matriciel