Journée
CMI, Château-Gombert, Marseille
https://www.i2m.univ-amu.fr/perso/stephane.charpentier/Pages-journees-speciales/Journee-analyse-harmonique-2022/Journee-AH-2022.html
Date(s) : 05/12/2022 iCal
Toute la journée
Journée d’Analyse Harmonique 2022
Marseille – Lundi 5 décembre 2022
Salle de séminaire du CMI (plan d’accès)
Organisateurs: A. Borichev, S. Charpentier, H. Youssfi, R. Zarouf
— 10h-11h – John McCarthy, St Louis et Paris (website)

The Hardy-Weyl algebra and Monomial Operators
Résumé: The Weyl algebra is the algebra generated by the operators of differentiation and multiplication by x. It is much studied in algebra and analysis. What happens if you replace the unbounded differentiation operator by a bounded integral operator, like the Volterra operator V or the Hardy operator H, where V and H are operators on L2[0,1] given by
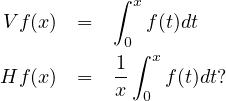
We shall discuss the algebra generated by multiplication by x and H, which we call the Hardy-Weyl algebra. We shall also discuss other operators T on L2[0,1] that have the property that they take monomials to multiples of other monomials, i.e. Txn = cnxpn.
This is joint work with Jim Agler.
— 11h15-12h15 – Nikolaos Chalmoukis, Sarrebruck (website)

The exceptional sets of the Drury Arveson space
Résumé: A classical theorem of Fatou [1] says that a function in the Hardy space of the disc has non tangential limits at almost every boundary point. Conversely for every compact set of Lebesgue measure zero in the boundary of the unit disc there exists a function in the Hardy space which fails to have non tangential limits exactly on this set. So we say that the exceptional sets are exactly the sets of Lebesgue measure zero.
In the unit ball of C^n there are two (different) spaces which play the role of the Hardy space in the unit disc. One is the Hardy space of the ball and the other one is the Drury Arveson space. For the first one, exceptional sets in the sense of Fatou have been characterized by Korányi [2].
In this talk we will give a characterization of the exceptional sets of the Drury Arveson space by introducing a new potential theory on the boundary of the unit ball in C^n or equivalently in the Heisenberg group.
[1] P. Fatou, (1906) Séries trigonométriques et séries de Taylor, Acta Mathematica, Acta Math. 30, 335–400.
[2] A. Korányi, (1969). Harmonic Functions on Hermitian Hyperbolic Space. Transactions of the American Mathematical Society, 135, 507–516.
12h40 – 14h20 — Déjeuner
— 14h30-15h30 – Myrto Manolaki, Dublin (website)

A strong form of Plessner’s theorem and applications
Résumé: Let f be a holomorphic function on the unit disc. According to Plessner’s theorem, for almost every point z on the unit circle, either (i) f has a finite nontangential limit at z, or (ii) the image f(S) of any Stolz angle S at z is dense in the complex plane. In this talk, we will see that condition (ii) can be replaced by a much stronger assertion. It turns out that this strong form of Plessner’s theorem and its harmonic analogue on halfspaces improve classical results of Spencer, Stein and Carleson. Moreover, after a brief overview of the theory of universal Taylor series, we will see how our main theorem strengthens a result about their boundary behaviour. (Joint work with Stephen Gardiner)
— 15h45-16h45 – Konstantinos Maronikolakis, Dublin (researchgate)
Properties of Abel Universal Functions
Résumé: In 2020, S. Charpentier showed that, for every sequence ρ = (ρn)n in [0, 1) with ρn → 1 as n →∞, there exist holomorphic functions f in the unit disk such that, for any proper compact subset K of the unit circle and any continuous function h on K, there exists a subsequence (ρλn)n of ρ such that |f(ρλnζ) –ϕ(ζ)|→ 0 as n →∞ uniformly for ζ ∈ K. We call these functions Abel universal. I will discuss properties of Abel universal functions and in particular their similarities and differences with the universal Taylor series, which are well studied in the field of universality. I will also present analogues of Abel universal functions for the Hardy, Bergman and Dirichlet spaces.
Emplacement
Site Nord, CMI, Salle de Séminaire R164 (1er étage)
Catégories