Julian Hennicker
University of Geneva
https://www.researchgate.net/scientific-contributions/Julian-Hennicker-2080599622
Date(s) : 28/03/2023 iCal
11 h 00 min - 12 h 00 min
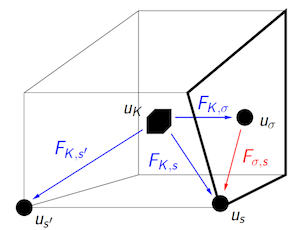
Models that contain thin heterogeneous layers provide particular challanges for their numerical solution, as they require anisotropic and/or very small mesh cells for a geometrical representation of the layers. This situation most prominently occurs in subsurface flow applications, where the thin heterogeneous layers are called fractures, and they are surrounded by the so-called rock matrix. Such models are unpracticable for real life simulations, and one might consider reduced models, which represent the fractures as hypersurfaces, embedded in the matrix domain. These reduced models are called in the literature mixed- or hybrid-dimensional models, or Discrete Fracture Matrix models. In this presentation, I will show a new approach to develop and analyze reduced order models for general linear elliptic problems. The focus lies on the derivation of coupling conditions, which have to be satisfied by the traces of the solutions for the matrix domain on each side of the matrix-fracture interfaces. Let it be emphasized that we are not only interested in the derivation of coupling conditions that have to be satisfied in the limit of vanishing aperture, but in particular with the derivation of coupling conditions that have to hold up to a certain order of the aperture, which in turn occurs as a model parameter in the reduced model. The idea is to first use a Fourier transform in the fracture tangential direction, which allows us to eliminate the fracture unknowns and to derive exact coupling conditions between the matrix subdomains, a technique which can be regarded as a continuous analogue to a Schur complement of the fracture unknowns onto the matrix-fracture interfaces, and which is frequently used in domain decomposition to derive coupling conditions for optimal or optimized Schwarz methods. Reduced order coupling conditions are then obtained by truncating the asymptotic expansions of the exact conditions at the desired order. This approach allows us in a second step to derive error estimates for the reduced order solutions, in terms of powers of the fracture aperture, a result which was still missing in the literature. Numerical tests will illustrate the results.
Emplacement
Site Nord, CMI, Salle de Séminaire R164 (1er étage)
Catégories