Supplementary material for the paper
by
S. Molla and B. Torrésani
abstract
This paper reports on recent results related to audiophonic signals
encoding using time-scale and time-frequency transform. More precisely,
non-linear, structured approximations for tonal and transient
components using local cosine and wavelet bases will be described,
yielding expansions of audio signals in the form
tonal
+ transient + residual
We describe a general formulation involving hidden Markov models,
together with corresponding rate estimates. Estimators for the balance
transient/tonal are also discussed.
Motivation, Illustration:
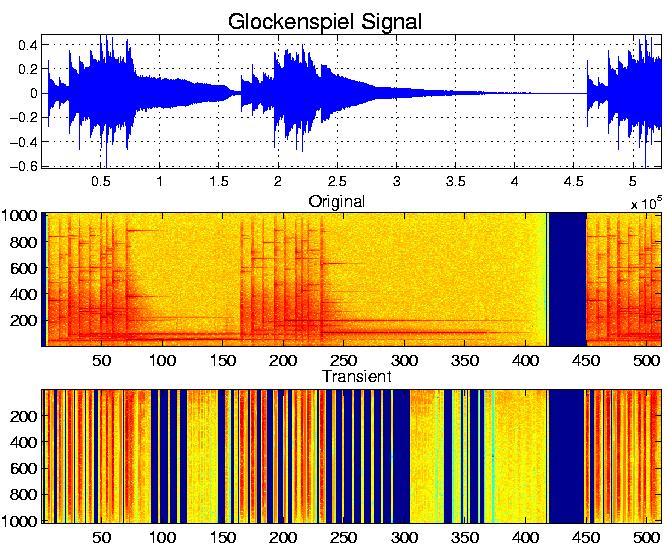
Sparsity is not enough to separate transients from tonals: The figure
below represents a glockenspiel signal (top)
and the logarithm of the modulus of MDCT coefficients (middle); even
though MDCT is a priori more adapted to the estimation of the tonal
layer, "vertical" chains of large MDCT coefficients are nevertheless
present, which do not correspond to tonals. A simple thresholding of
MDCT coefficients clearly does not separate between these "vertical"
and "horizontal" parts of the MDCT coefficients. The introduction of
structures in the estimation procedure allows one to keep only
"horizontal ridges" of large MDCT coefficients (bottom).

After substraction of the estimated tonal component, the same
representation of the residual (bottom figure below) only shows the
"vertical" structures, i.e. transients.
Model:
The signal is modeled (HWAM: Hybrid Waveform Audio Model) as a linear
combination of a few wavelets and
a few local cosines (MDCT basis functions), whose index sets belong to
transient and tonal significance maps. The tonal significance map is
assumed to form "horizontal ridges" (of significant MDCT coefficients),
while the transient significance map is supposed to form "trees" of
significant wavelet coefficients.
The observations are the samples of the hybrid signal, which may be
represented by "observed" MDCT coefficients (i.e. the MDCT coefficients
of the hybrid signal... not those of its MDCT part). The main idea is
that these observed coefficients may have two different types of
behaviors:
- if the corresponding index belongs to the initial tonal
significance map, the MDCT coefficient is expected to be large.
- otherwise, the MDCT coefficient originates from the wavelets (the
transient part), and is expected to be small.
To resolve the ambiguities, the structures (i.e. persistence
properties) are exploited: roughly speaking, an MDCT coefficient is
considered belonging to the tonal layer if it is large enough, and if
its neighbours (in time) belong to the tonal layer. A similar strategy
is used to select the wavelet coefficients for describing transients.
Tonal layer:
The signal is first expanded on a local cosine (MDCT) basis, and the
largest coefficients are retained, provided they satisfy a time-persistence condition. More
precisely, at each frequency, coefficients are modeled using a mixture
of Gaussian random variables: T-type
(T for tonal) coefficients have large variance, and R-type coefficients (R for
residual, originating from the wavelet part, and non-sparse components,
noise,...)
have small variance. Time persistence is modelled by a Markov chain.
The parameters of the model are the variances of the normal
distributions at each frequency, and the probabilities of transition T
-> R and R -> T.
Parameters are estimated using an adapted EM algorithm, and the
locations of T-type coefficients are estimated by thresholding
posterior probabilities. The tonal layer is reconstructed as the
projection of the signal onto the linear span of MDCT atoms
corresponding to T-type coefficients. A nontonal part of the
signal is obtained by substracting the tonal layer from the signal.
Transient layer:
The nontonal part is expanded onto a wavelet basis, and the largest
coefficients are retained, provided they satisfy a scale-persistence
condition. More precisely, at each scale, coefficients are modeled
using a mixture of Gaussian random variables: T-type (T now stands for transient)
coefficients have large variance, and R-type
coefficients (R for residual) have small variance. Scale-persistence is
modelled by a Markov chain on the dyadic tree naturally associated with
the wavelet basis. The parameters of the model are again the variances
of the normal distributions at each frequency, and the probability of
transition T -> R (the transition R -> T is forbidden,
which ensures connectedness of the tree of T-type coefficients).
Again, parameters are estimated using an adapted EM algorithm, and the
locations of T-type coefficients are estimated by thresholding
posterior probabilities. The transient layer is reconstructed as the
projection of the signal onto the linear span of wavelets corresponding
to T-type coefficients. A residual part of the signal is obtained
by substracting the transient layer from the nontonal signal.
Residual:
The residual is modeled using standard LPC procedure.
Hybrid decomposition
Test signal: mamavatu
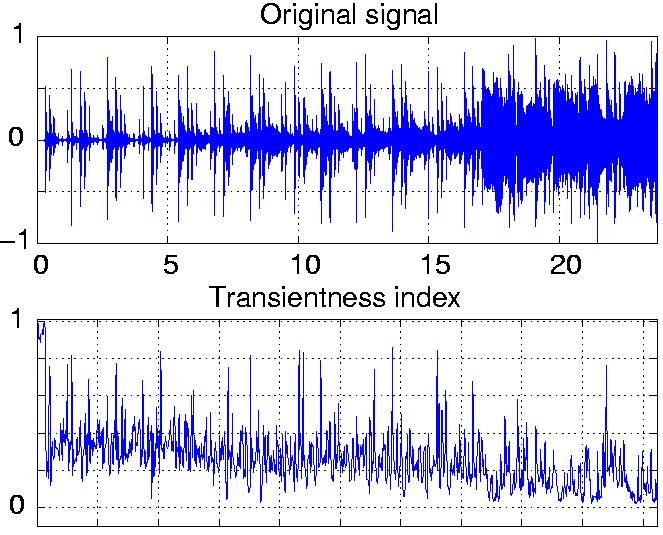
Transientness index
First, a transientness index is estimated (see the article
and supplementary
material for details), which provides an oracle for
the proportion of the bit budget to be spent on the transient part:
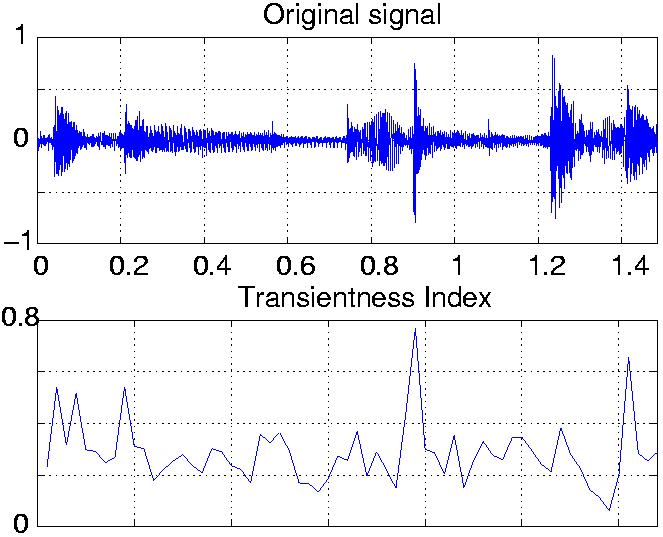
same index on a smaller portion of the signal:
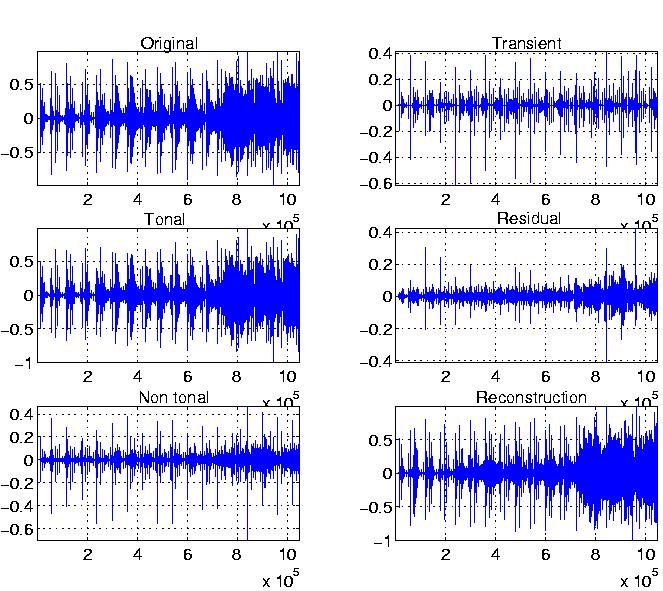
Hybrid decomposition:
Given a global bit budget, split into transient bit budget, tonal bit
budget as prescribed by the transientness index, and residual bit
budget (constant), the three layers are estimated, and are displayed
below:
Sound files:
the mamavatu signal
Another example: the glockenspiel signal




