Supplementary material for the article

Determining local transientness of audio signals
by
S. Molla and B. Torrésani

(site under construction)

Abstract

Using information theoretic criteria and MDCT and wavelet transforms, a time dependent transientness index and a time-dependent tonality index may be associated with audio signals. This finds applications in several contexts, in particular hybrid audio coders, where dynamic bit budget allocation to tonal and transient layers is necessary. Extensions to similar ideas in image modeling and coding are also possible.

Transientness and tonality indices

Given a signal model of the form

signal = tonal + transient + residual

in mathematical terms, a (sparse) sum of wavelets and windowed cosine functions, with independent normally distributed coefficients, it may be shown that the sum of logarithms of squares of the wavelet coefficients of such a compount signal provides estimates on the "size" of the tonal (i.e. local sine) layer. Similarly, the sum of logarithms of squares of the local cosine coefficients of the signal yields estimates on the "size" of the transient (i.e. wavelet) layer. From this, the relative importances of tonal and transient layers may be computed.

Real sound examples from the paper:

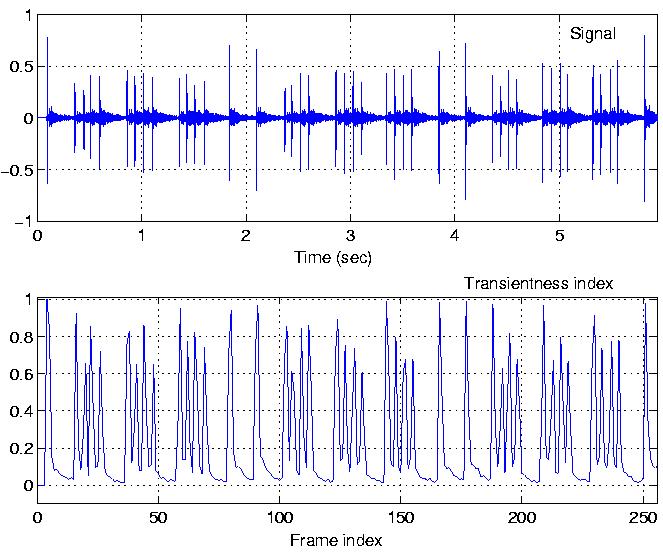
The castagnette signal:

The castagnette signal, and the corresponding time-varying transientness index

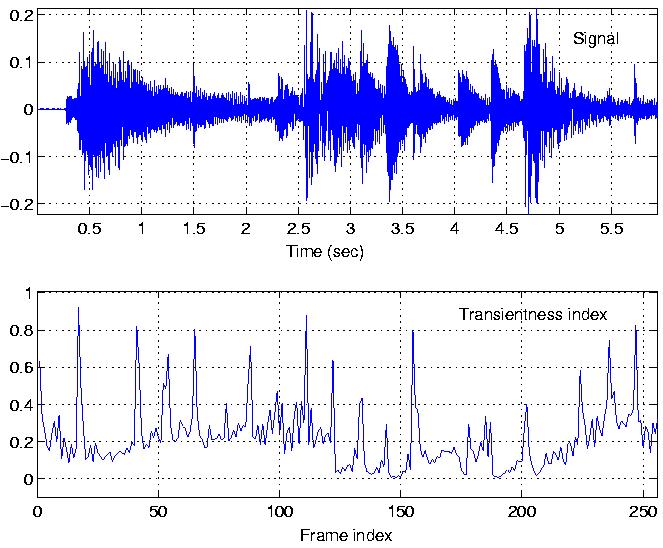
The jazz signal

The jazz signal, and the corresponding time-varying transientness index

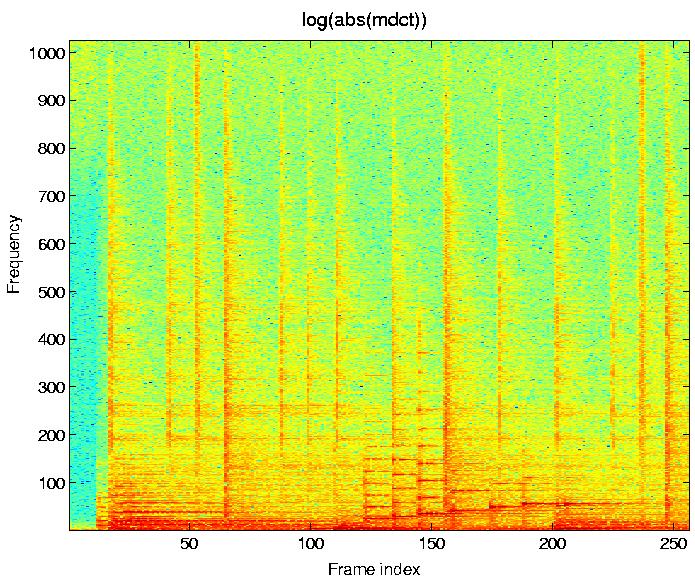
Corresponding time-frequency representation

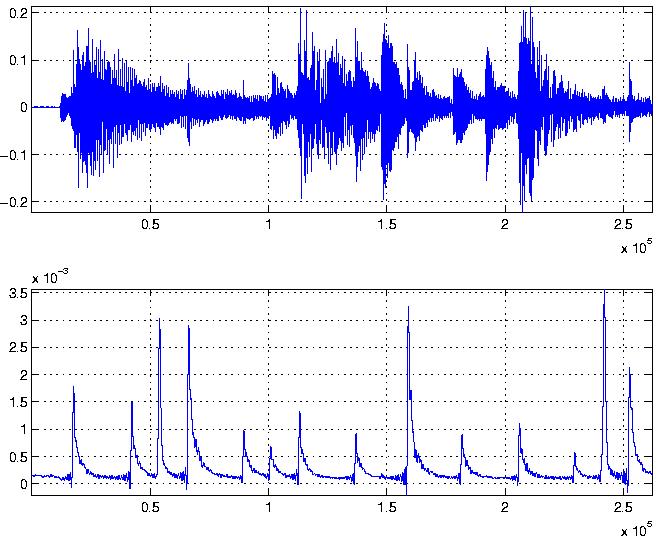
Transient detection by envelope of high-pass filtered version