Matrices booléennes

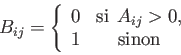
Il est possible de définir des matrices dont les termes ne sont pas des réels, comme par exemple, des matrices d'entiers positifs (de type uint8, entier non signés de taille 8), de booléens, de caractères,...

Les matrices booléennes sont des matrices dont les termes valent 0 (pour faux) ou 1 (pour vrai). On les obtient généralement en appliquant des opérateurs logiques aux matrices. Exemple :

A = [3 2 1;-1 -2 1];
B = A>0
B =

   1   1   1
   0   0   1

Dans cet exemple, on peut remarquer que le condition logique ("être supérieur à 0") est vérifiée terme à terme. La matrice B correspond à

$$B_{ij} = \left\{ \begin{array}{cc} 0 & \mathrm{si} \:\: A_{ij}>0,\\ 1 & \mathrm{sinon} \end{array} \right.$$

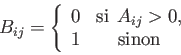
D'une manière générale, l'opérateur logique s'applique terme à terme (opération ointée) et les valeurs de la matrice booléenne indique si pour chaque terme la condition est vraie (1) ou fausse (0).

On peut également se servir de matrices booléennes pour accéder aux termes d'une matrice vérifiant une certaine condition. Exemple

A(B)
ans =

   3
   2
   1
   1

Les principaux opérateurs logiques sont

<	"strictement inférieur à"
>	"strictement supérieur à"
<=	"inférieur ou égal à"
>=	"supérieur ou égal à"
==	"égal à"
~=	"différent de"
&	et logique
|	or logique
~	non logique