Opérations élémentaires sur les matrices

En matlab, les opérations * (multiplication), + (addition) et - (soustraction) sont des opérations matricielles.
L'addition (resp. la soustraction) se font terme à terme : Etant données A et B deux matrices de même taille, la matrice

C = A+B   %%%resp.  C=A-B 

produit une matrice de même taille que A et B définie par

$$c_{ij} = a_{ij} + b_{ij} \:\:\: \mathrm{resp.} \:\: c_{ij} = a_{ij} - b_{ij}.$$

Etant données une matrice A de taille lxm et une autre B de taille mxn,

C = A*B

donne une matrice de taille lxn définie par

$$c_{ij} = \sum_{k=1}^m a_{ik} b_{kj}.$$

On peut aussi réaliser une opération de multiplication terme à terme sur des matrices de même taille (multiplication pointée). En écrivant

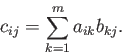
C=A.*B;

on calcule la matrice C qui a pour terme

$$c_{ij} = a_{ij} b_{ij}.$$

Cela nécessite que A et B aient la même taille.

L'opération exposant (notée $\hat{}$) est conçue selon les mêmes principes que la multiplication. Etant donné une matrice carrée A et un entier relatif non nul n, le code

B=A^n;

produit la matrice

$$B=A^n=A \cdots A$$

tandis que le code

B=A.^n;

produit la matrice B de terme

$$B_{ij} = a_{ij}^n$$

L'opération / ne correspond pas à une division. En écrivant le code

x=A/b;

on résout le système linéaire

$$Ax=b.$$

Il existe cependant une opération de division pointée. Etant données A et B deux matrices de même taille, B ne comportant pas de termes nuls, le code

C=A./B;

produit une matrice C ayant pour terme

$$C_{ij} = A_{ij}/B_{ij}.$$