Fonctionalités de base

Matlab et octave intègrent un ensemble de fonctionnalités qui permettent de calculer rapidement des propriétés associées aux matrices.

Le calcul du déterminant et de la trace d'une matrice peuvent se faire à l'aide des commandes det et trace, respectivement.

Une matrice A de taille nxp représente une application linéaire

$$f : \mathbb{R}^p \longrightarrow \mathbb{R}^n$$

dans des bases particulières des espaces de départ et d'arrivée. L'image Im(f) et le noyau Ker(f) de cette application f sont définies par

$$\begin{array}{l} \mathrm{Im}(f) = \{ f(x), x \in \mathrm{R}... ...R}^n, f(x)=0 \} =\{ x \in \mathrm{R}^n, Ax=0 \}. \end{array}$$

Ces deux ensembles sont des sous-espaces vectoriels. La dimension de Im(f) correspond au rang(f).

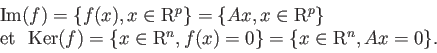
En matlab et octave, on peut calculer le rang d'une matrice au moyen de la commande rank.

On peut en outre déterminer une base orthonormée de l'espace Im(f) à l'aide de la commande orth. Par exemple,

A=[1 2 1; 1 2  1 ; 1 1  0 ; 1 1 0 ] ; 
BaseIm = orth(A);
Rang = size(BaseIm,2)
Rang = rank(A)

Comme dans l'exemple ci-dessous, on peut également calculer une base de l'espace noyau Ker(f) à l'aide de la commande null.

BaseKer = null(A);
DimKer = size(BaseKer,2);