m = BetaAdicMonoid(1/(1+I), {0,1}); m
Monoid of b-adic expansion with b root of x^2 - x + 1/2 and numerals
set {0, 1}
|
m.relations_automaton()
Finite automaton with 1 states |
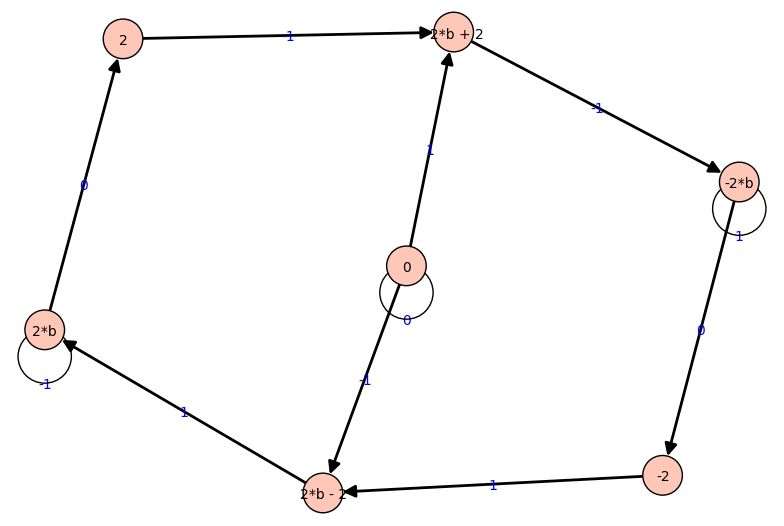
a = m.relations_automaton(ext=True); a
Finite automaton with 7 states |
a.plot()
|
|
p1 = m.plot(); p1
|
|
.png)
# compute the intersection of the two subsets of the limit set
# corresponding to words with prefix 0 and words with prefix 1
ssi = m.intersection_words([0], [1]); ssi
Finite automaton with 21 states |
# plot the intersection
p2 = m.plot(ss=ssi, n=19); p2
|
|
.png)
p1+p2
|
|
.png)
# compute the Hausdorff dimension of the intersection
m.critical_exponent_free(ss=ssi)
log(y)/log(|b|) where y is the max root of x^3 - x^2 - 2 1.52362708620249 |
|
|
m=BetaAdicMonoid(b,{0,1});m
Monoid of b-adic expansion with b root of x^4 + x^3 - x + 1 and
numerals set {0, 1}
|
|
|
# A substitution
s = WordMorphism('a->ab,b->c,c->d,d->e,e->a'); s
WordMorphism: a->ab, b->c, c->d, d->e, e->a |
p1 = s.rauzy_fractal_plot(); p1
|
|
.png)
# Get the beta-adic monoid with subshift whose limit set is the Rauzy fractal
m = s.rauzy_fractal_beta_adic_monoid(); m
Monoid of b-adic expansion with b root of x^3 - x - 1 and numerals
set {0, 1} with subshift of 5 states
|
# compute the intersection of the two subsets of the limit set
# corresponding to words with prefix 0 and words with prefix 1
ssi = m.intersection_words([0], [1]); ssi
Finite automaton with 80 states |
p2 = m.plot(ss=ssi, n=40); p2
|
|
.png)
p1+p2
|
|
.png)
# compute the Hausdorff dimension of the intersection
m.critical_exponent_free(ss=ssi)
log(y)/log(|b|) where y is the max root of x^5 - x - 1 1.10026338504521 |
|
|
P = x^4 + x^3 - x + 1
b = P.roots(ring=QQbar)[2][0]; b
0.5661209411559501? - 0.4588214646725570?*I |
m = BetaAdicMonoid(b, {0,1}); m
Monoid of b-adic expansion with b root of x^4 + x^3 - x + 1 and
numerals set {0, 1}
|
m.plot()
|
|
.png)
m.relations_automaton().plot()
|
|
.png)
m.reduced_words_automaton().plot()
|
|
.png)
m.critical_exponent()
log(y)/log(|b|) where y is the max root of x^5 - 2*x^4 + 2 1.88549430475576 |
[a[0] for a in (x^5 - 2*x^4 + 2).roots(ring=CC)]
[-0.910472093668948, 1.30022153937654, 1.81617880630727, -0.102964126007430 - 0.958969280993209*I, -0.102964126007430 + 0.958969280993209*I] |
#produit de Mahler d'un entier algébrique
def mahler(P):
r=P.roots(ring=CC)
return prod([abs(a[0]) for a in r if abs(a[0]) > 1])
|
|
mahler(m.b.minpoly()) # on a bien 1.88320350591353 >= 1.81617880630727
1.88320350591353 |
|
|
m = BetaAdicMonoid(3/2, {0, 1, 6}); m
Monoid of 3/2-adic expansion with numerals set {0, 1, 6}
|
m.relations_automaton().plot()
|
|
.png)
ar = m.reduced_words_automaton(); ar.plot()
|
|
.png)
#initial states
ar.I
[0] |
#final states
ar.F
[0, 1, 2, 3] |
ar.adjacency_matrix()
[2 1 0 0] [2 0 1 0] [0 1 0 1] [0 0 1 1] |
|
|