Automata and Regular language in Sage¶
Author: Paul Mercat, and Dominique Benielli Labex Archimede - I2M - AMU Aix-Marseille Universite
Automata and Regular language¶
Automata are sort of machines that can realize linear time calculation only requiring a fine memory. For more details see [Ca].
Automata¶
Definition of an automaton¶
We call automaton a quintuplet \(A := (\Sigma,\mathrm{Q},\mathrm{T},\mathrm{I},\mathrm{F})\), where
- \(\Sigma\) is a finite set called alphabet,
- \(\mathrm{Q}\) is a finite set of states,
- \(\mathrm{T} \subseteq \mathrm{Q} \times \Sigma \times \mathrm{Q}\) is a finite set of transitions,
- \(\mathrm{I} \subseteq \mathrm{Q}\) is a finite set of initial states,
- \(\mathrm{F} \subseteq \mathrm{Q}\) is a finite set of final states.
- The automaton is deterministic if
- \(\sharp \, \mathrm{I} = 1\) and
- \(\left[ \left( p, a, q \right) \in \mathrm{T} \quad and \quad \left(p, a, r \right) \in \mathrm{T} \right] \Rightarrow q = r\)
So, when the automaton \(A\) is deterministic, \(\mathrm{T}\) is the graph of a partial function of transition \(\mathrm{Q} \times \Sigma \rightarrow \mathrm{Q}\), and there is only one initial state. We will sometimes consider infinite automata, that is, automata for which set of states \(\mathrm{Q}\) is infinite.
Note
We often denote \(p \overset{a}{\rightarrow} q \quad\) if \(\quad \left( p, a, q \right) \in \mathrm{T}\).
Note
For an alphabet \(\Sigma\), we note \(\Sigma^* := \Sigma^{(\mathbb N)}\) the set of finish words. For a word \(u \in \Sigma^{*}\), we note \(u^* := \cup_{n \in \mathbb N} = \{ u^n \}^*\).
Graphical representation¶
Automata are represented as graphs whose edges are labeled by letters of the alphabet.
On the drawings in this section, the initial state is in bold, and the final states are the circles drawn with a double line
Deterministic automaton can be created in sage by the use of sage.combinat.words.DeterministicAutomaton as follow:
sage: a = DeterministicAutomaton([(0,0,'(0,0)'),(0,0,'(1,1)'),(0,3,'(1,0)'),(1,2,'(0,1)'),(2,0,'(0,1)'),(2,1,'(1,1)'),(2,1,'(0,0)'),(3,4,'(0,1)'),(4,3,'(0,0)'),(4,0,'(1,0)')])
sage: a.set_final_states([0])
sage: a.set_initial_state(0)
sage: a.add_transition(0,'(1,0)',1)
sage: a.plot().show()
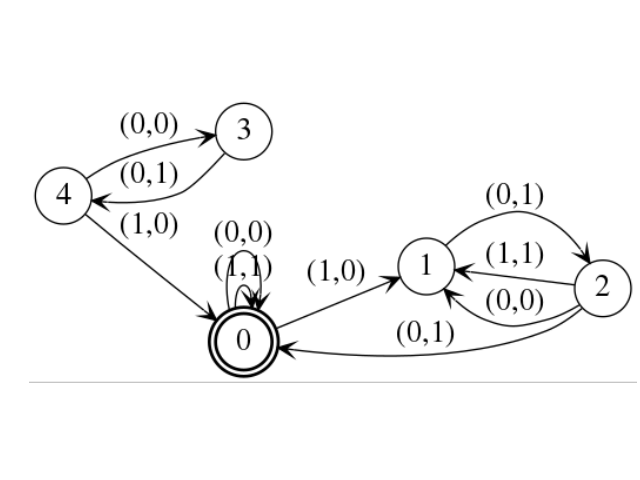
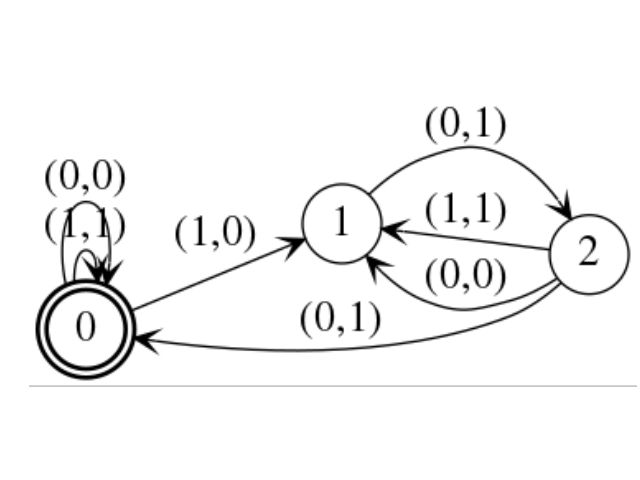
Automaton with states {0, 1, 2, 3, 4}, alphabet {(0,0), (0,1), (1,0), (1,1)}, set of inital states {0}, and set of final states {0}.
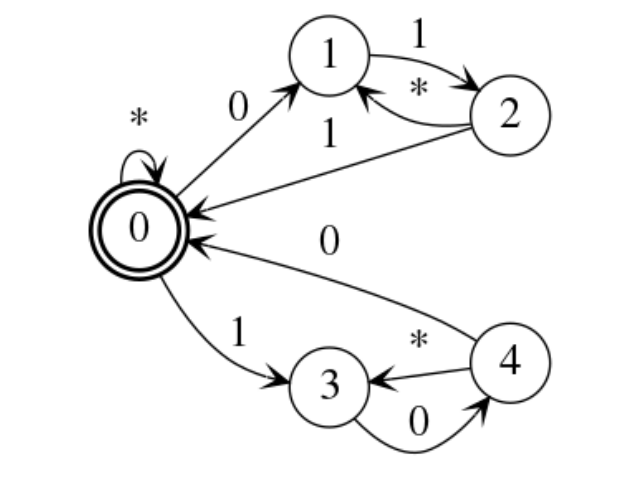
Automaton with states {0, 1, 2, 3, 4}, alphabet {0, 1, *}, set of inital states {0} and set of final states {0}.
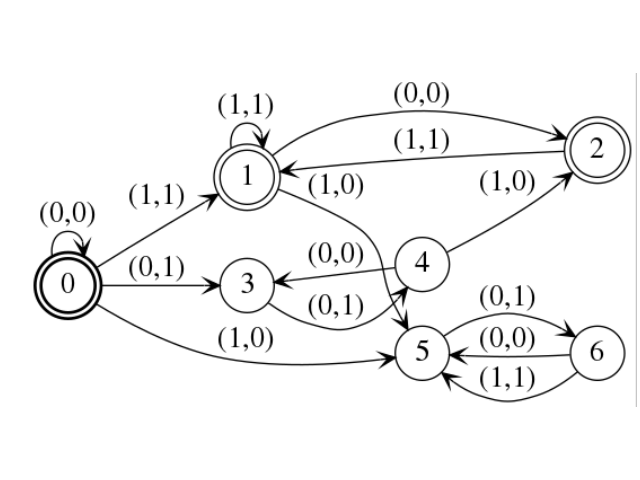
Automaton of states {0, 1, 2, 3, 4, 5, 6}, alphabet {(0,0), (0,1), (1,0), (1,1)}, for inital state {0} and finals states {0, 1, 2}.
And there are also deterministic automata generators that can be used. Automaton recognizing a single word:
sage: a = dag.Word("gabian")
sage: a.plot()
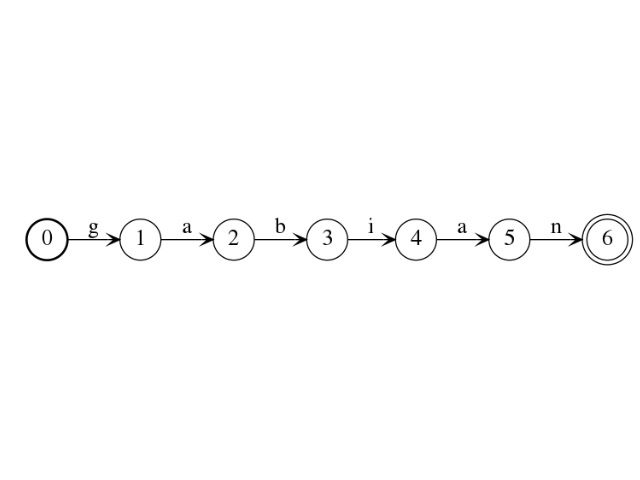
Automaton recognizing every words over a given alphabet:
sage: a = dag.AnyWord("abc")
sage: a.plot()
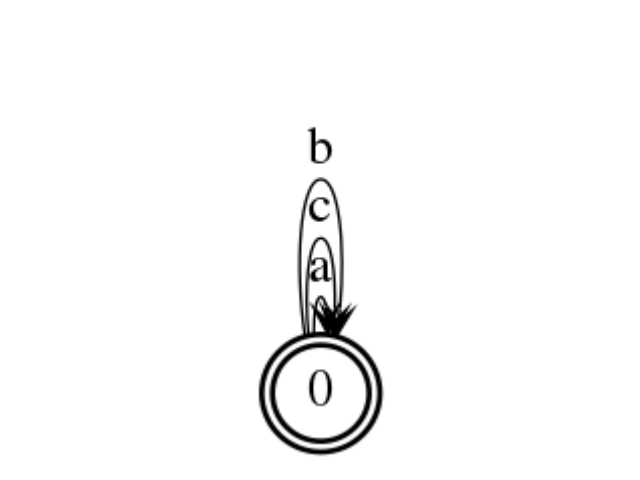
Language¶
Definition: regular language¶
A language is a set of words over a given alphabet. The language recognized by an automaton \(A = (\Sigma, Q, T, I, F)\) is the set \(L_A\) of words \(a_1 \dots a_n \in \Sigma^*\) such that there exists a path \(\mathrm{I} \ni q_0 \xrightarrow{a_1} q_1 \xrightarrow{a_2} \dots \dots \xrightarrow{a_{n-1}} q_{n-1} \xrightarrow{a_n} q_n \in \mathrm{F}\) in the automaton \(A\) from an initial state to an end state.
A word \(u \in \Sigma^*\) is recognized by the automaton \(A\) if we have \(u \in L_A\).
A word \(a_1 \dots a_n\) is therefore recognized by the automaton \(A\) if there exists a path in the graph, labeled by \(a_1, a_2, \dots, a_n\), starting from an initial state and ending to a final state.
Note
If the automaton is deterministic, the path is determined by the sequence of labels.
Examples¶
some examples of automaton.
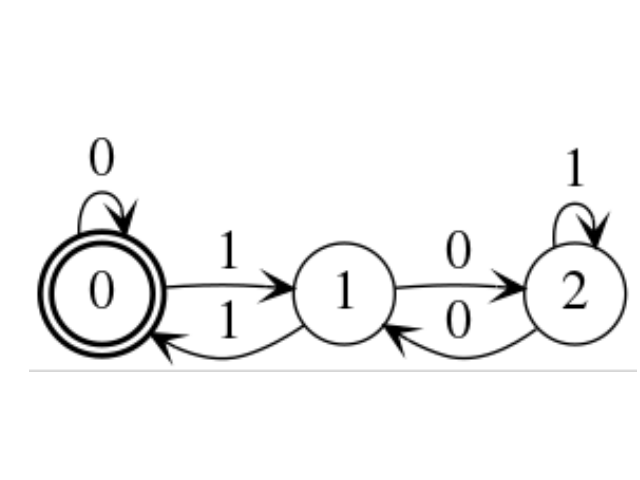
The above automaton recognize all the numbers written in binaries that are divisible by 3.
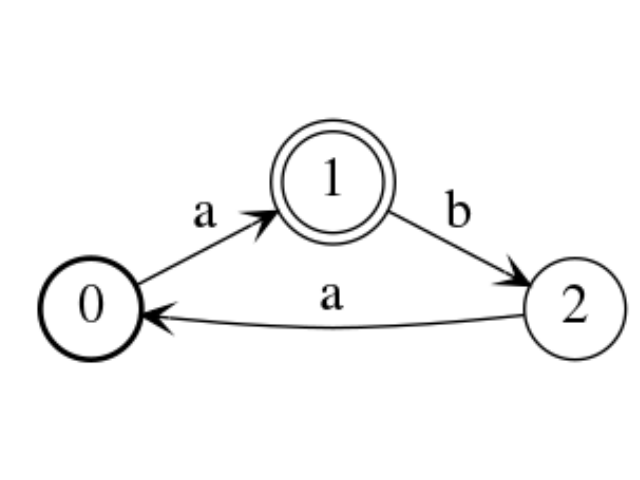
The above automaton recognize the set of words of the form \(a(baa)^n\).
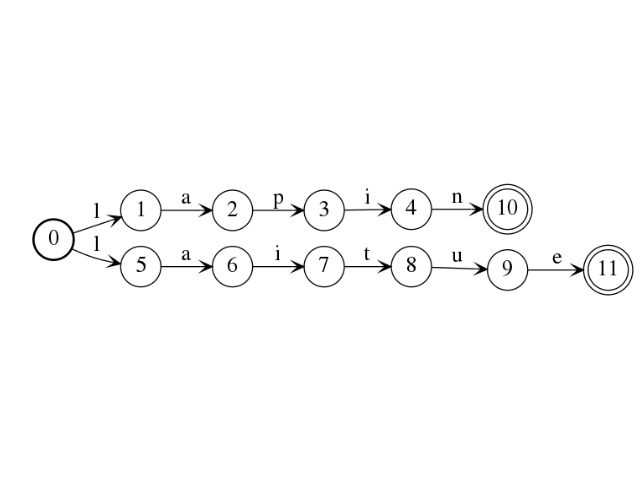
The above non deterministic automaton recognize the set of words
{lapin, laitue}. Obtained with the followed code and the class sage.combinat.words.NFastAutomaton:
sage: a = DeterministicAutomaton([(0,1,'l'),(1,2,'a'),(2,3,'p') ,(3,4,'i'),(4,10,'n'),(0,5,'l'),(5,6,'a'),(6,7,'i'),(7,8,'t'),(8,9,'u'),(9,11,'e')])
sage: a.set_final_states([10,11])
sage: a.set_initial_state(0)
sage: b = CAutomaton(a)
sage: b.add_transition(0,'l',1)
sage: b.plot().show()
Equivalent automata¶
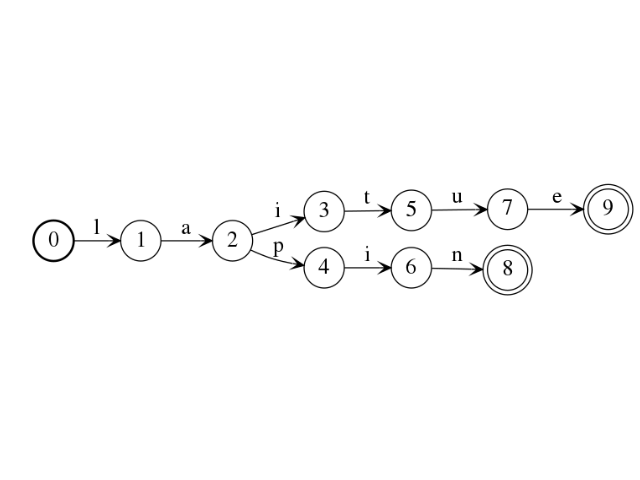
Two automata \(A\) and \(A'\) are equivalent if they recognize the same language $L_A = L_{A’}$. Automaton equivalent to the previous one is:
sage: c = b.determinise()
sage: c.plot().show()
Note
Any automaton is equivalent to a deterministic automaton.
Minimal automata¶
A minimal automaton of an automaton \(A\) (or the minimal automaton of the corresponding language) is a deterministic automaton \(A '\), equivalent to \(A\), and having a minimal number of vertices for these properties.
Note
The minimal automaton is unique. Moreover, if the automaton \(A\) is deterministic, then the minimal automaton is obtained like the quotient of the automaton \(A\) by an equivalence relation consisting of identifying vertices between them.
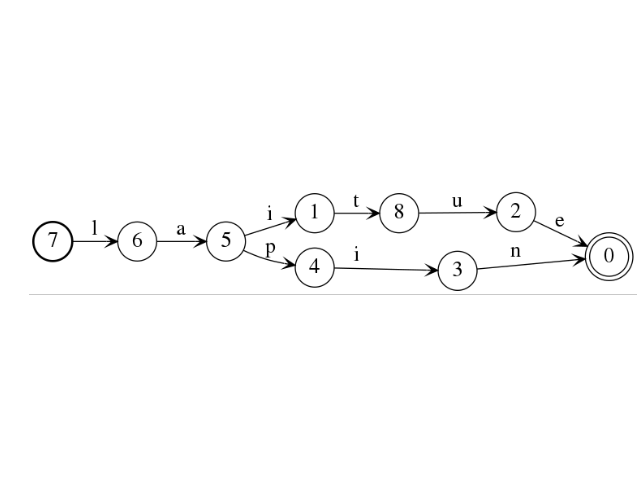
The minimal automaton of the language {lapin, laitue} is the following:
sage: d = c.minimise()
sage: c.plot().show()
Transpose(e.I. mirror) automaton¶
The transposed (or the mirror) automaton of an automaton \(A := (\Sigma,\mathrm{Q},\mathrm{T},\mathrm{I},\mathrm{F})\) is the automaton
Note
The language recognized by the transposed automaton \(A^t\) is the transpose of the recognized language by the initial automaton \(A\).
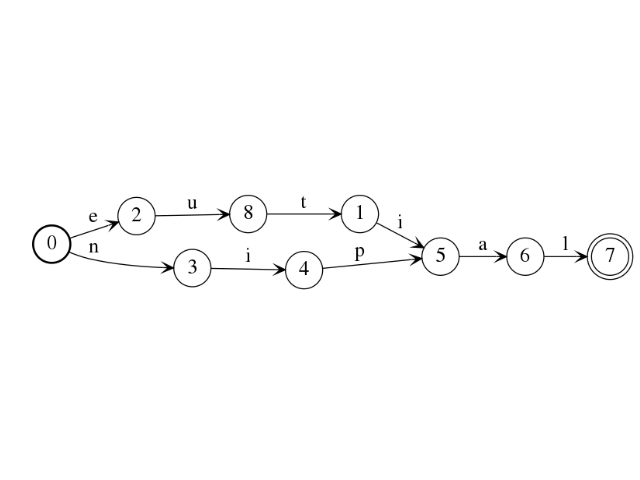
The transposed of the minimal automaton of the language {lapin, laitue} is:
sage: b = a.mirror()
sage: b.plot().show()
Pruned automaton¶
The pruned automaton is the automaton restricted to states that are reachable from an initial state, and from which we can go to a final state.
Note
A (possibly infinite) deterministic pruned automaton, and with a deterministic transposed is minimal. In particular, if it is infinite, the language that it recognizes is not regular.
Example of non-pruned automaton:
sage: a = DeterministicAutomaton([(0,0,'(0,0)'),(0,0,'(1,1)'),(0,3,'(1,0)'),(1,2,'(0,1)'),(2,0,'(0,1)'),(2,1,'(1,1)'),(2,1,'(0,0)'),(3,4,'(0,1)'),(4,3,'(0,0)'),(4,0,'(1,0)')])
sage: a.set_final_states([0])
sage: a.set_initial_state(0)
sage: a.add_transition(0,'(1,0)',1)
sage: a.plot().show()
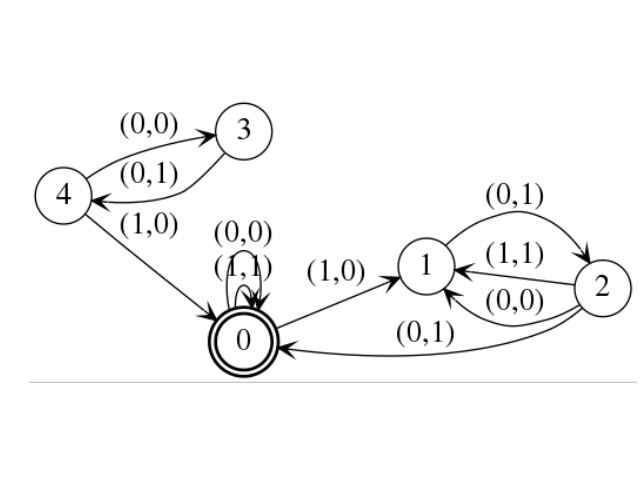
And the corresponding pruned automaton:
sage: b = a.prune()
sage: b.plot().show()
This automaton can be seen below: