LES ONDELETTES
A. Grossmann et B. Torrésani
Centre de Physique Théorique,
CNRS-Luminy, Case 907, 13288 Marseille Cedex 09
et
Laboratoire d'Analyse, Topologie et Probabilités,
CMI, Université de Provence, 31 rue Joliot Curie, 13452
Marseille Cedex 13
1. LA MUSIQUE DES MATHEMATIQUES
2. UNE REPRESENTATION EFFICACE
3. DES ALGORITHMES RAPIDES
4.
UNE APPLICATION SPECTACULAIRE: LA COMPRESSION DE DONNEES
5. AU DELA DES ONDELETTES
Encart 1: l'analyse de Fourier
Encart 2: décompositions en ondelettes.
Encart 3:
algorithmes pyramidaux.
Résumé:
Qu'y a-t-il de commun entre le stockage numérique des empreintes digitales effectué par le FBI, la compression des images pour la télévision haute définition et le téléphone vidéo, le stockage ou la transmission de résultats de mesures sismiques, l'analyse des grandes structures galactiques, la modélisation des cascades d'énergie dans des écoulements hydrodynamiques fortement turbulents, ou encore la détection des ondes gravitationnelles ? Fondamentalement rien, si ce n'est que tous ces problèmes (et bien d'autres encore) sont susceptibles d'être attaqués en utilisant une famille de méthodes, génériquement appelées méthodes temps-fréquence, et en particulier l'analyse par ondelettes.
L'analyse par ondelettes a été introduite au début des années 1980, dans un contexte d'analyse du signal et d'exploration pétrolière. Il s'agissait à l'époque de donner une représentation des signaux permettant de faire apparaître simultanément des informations temporelles (localisation dans le temps, durée) et fréquentielles, facilitant par là l'identification des caractéristiques physiques de la source du signal. Les ondelettes n'ont depuis lors cessé de se développer et de trouver de nouveaux champs d'application. C'est ainsi qu'est apparu un parallèle étonnant entre ces méthodes et des techniques développées à des fins totalement différentes en traitement d'images, mais aussi d'autres théories mathématiques poursuivant des objectifs sans aucun lien apparent (comme par exemple des problèmes d'analyse mathématique pure, ou d'autres liés au problème de la quantification de certains systèmes classiques, ou plus récemment des problèmes de statistiques).
Avec quelques années de recul, nous réalisons maintenant que ce sont ces origines "scientifiquement cosmopolites" qui ont donné à la théorie toute sa richesse et sa beauté, en même temps que ses vastes domaines d'application.
1. LA MUSIQUE DES MATHEMATIQUES
Qu'est-ce qu'une ondelette ? En schématisant à l'extrême, nous dirons qu'une ondelette est l'idéalisation mathématique d'une note de musique.
De même que l'on représente une oeuvre musicale sous forme de séries de notes portées sur une partition, on peut songer à utiliser des notes mathématiques pour représenter certains objets mathématiques, tels des fonctions ou signaux. De même qu'une note de musique est un morceau de son, apparaissant à un instant donné, d'une durée donnée, et d'une hauteur donnée, une note mathématique est un objet auquel l'on associe des caractéristiques physiques telles que leur localisation dans le temps, leur durée et leur hauteur.
Ces notes mathématiques sont à comparer aux sinusoïdes sur lesquelles repose l'analyse de Fourier (ou analyse spectrale) usuelle (voir encart). Dans un certain sens, une sinusoïde est une note totalement idéalisée, associée à une fréquence "infiniment pure", mais à laquelle l'on ne saurait affecter de notion temporelle précise (instant de départ, durée): une sinusoïde n'a ni début ni fin.
L'analyse de Fourier nous enseigne qu'un signal quelconque peut s'écrire comme une somme de telles sinusoïdes, de fréquences et d'amplitudes variables. Un signal est entièrement caractérisé par l'ensemble des amplitudes des sinusoïdes, qui forme ce que l'on appelle sa transformée de Fourier. La transformée de Fourier est porteuse de précieuses informations sur le signal analysé (elle contient en fait toutes les informations disponibles). On sait par exemple que si elle n'a que de faibles valeurs pour des valeurs élevées de la variable de fréquence, ceci signifie que le signal varie lentement. Inversement, si elle prend des valeurs importantes pour les hautes fréquences, le signal contient une quantité non-négligeables de hautes fréquences, et donc varie rapidement, au moins dans certaines zones. Et c'est précisément là que nous touchons du doigt l'une des limitations importantes de l'analyse de Fourier usuelle. La transformée de Fourier du signal est incapable de localiser les portions du signal dans lesquelles les variations sont rapides, ni celles où elles sont lentes.
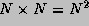
Figure 1: exemples d'ondes élémentaires:
vert: deux sinusoîdes de fréquences différentes; la fréquence mesure la vitesse des oscillations.
bleu: deux Gaborettes: fonctions élémentaires dont l'on fait varier la localisation (translation) ainsi que la fréquence (modulation), tout en gardant leur taille constante. Leur forme varie.
rouge: deux ondelettes: fonctions élémentaires dont l'on fait varier la localisation (translation) ainsi que la taille (dilatation ou contraction), tout en gardant leur forme constante. La dilatation s'accompagne d'une variation de la vitesse des oscillations, donc de la fréquence.
Un prototype d'analyse par ondelettes avait été proposé au milieu des années 1940 par le physicien D. Gabor (qui reçut par la suite le prix Nobel pour ses travaux sur l'holographie). Gabor suggérait de rendre locale l'analyse de Fourier, en s'aidant de fenêtres. Une fenêtre est une fonction régulière, lentement variable, et bien localisée (ce qui signifie qu'elle est nulle en dehors d'une certaine zone, son support). En multipliant la fonction étudiée par une fenêtre, on en obtient une version "locale", dont on peut déterminer le contenu fréquentiel par analyse de Fourier classique. On renouvelle alors l'opération en déplaçant la fenêtre d'analyse. L'ensemble de ces transformées de Fourier ainsi localisées forme la transformée de Gabor du signal, et fournit donc une analyse fréquentielle locale.
Signalons toutefois que cette opération est loin d'être innocente. Nous nous heurtons ici à une barrière infranchissable, connue sous le nom d'inégalités de Heisenberg et que l'on peut exprimer ainsi: ce que nous avons gagné en localité, en précision temporelle, est irrémédiablement perdu en précision sur les fréquences. En d'autres termes, en cherchant à préciser les notions temporelles, nous avons rendu floues les notions fréquentielles. Cette incertitude, pour limitante qu'elle soit, fait aussi la substance et la saveur de cette nouvelle problématique qu'est l'analyse temps-fréquence: il revient à l'utilisateur de décider quelle est la part de précision temporelle et de précision fréquentielle dont il a besoin.
L'analyse de Gabor a connu de multiples applications pratiques, notamment dans le domaine du traitement des signaux audiophoniques. On peut en particulier citer l'exemple du vocodeur de phase, qui connut de grands succès dans le domaine du traitement numérique de la parole. Son principe essentiel est que le signal de parole (c'est à dire les ondes de pression acoustique émises par l'appareil vocal du locuteur, et se propageant juqu'au tympan de l'auditeur) possède une représentation de Gabor très caractéristique, à partir de laquelle il peut être possible (pour des experts, ou pour des programmes informatiques très sophistiqués) d'identifier soit le locuteur, soit la phrase prononcée. Un autre exemple d'application de l'analyse de Gabor est fourni par les problèmes de détection de signaux, en acoustique sous marine par exemple. De tels signaux prennent souvent la forme de tons assez courts, dont la fréquence peut varier en fonction du temps. Il est bien évident que la loi de variation de la fréquence en fonction du temps est porteuse d'informations, très difficiles à extraires par analyse de Fourier. L'analyse de Gabor fournit souvent une réponse satisfaisante à ce problème.
De même que la transformée de Fourier, la transformée de Gabor d'un signal contient toutes les informations portées par le signal. Par conséquent, le signal peut être reconstruit à partir de sa transformée de Gabor. Cette reconstruction est remarquablement simple: le signal peut être synthétisé comme somme de Gaborettes, qui ne sont autres que des sinusoïdes localisées par des fenêtres du même type que celles utilisées pour la transformation de Gabor. A chacune de ces Gaborettes sont attachés une fréquence et un temps bien déterminés. Le poids d'une Gaborette dans un signal n'est autre que la valeur de sa transformée de Gabor pour la fréquence et le temps correspondants.
L'analyse par ondelettes, proposée initialement par J. Morlet, est plus récente (quoique l'on puisse lui trouver des origines aussi anciennes que l'analyse de Fourier à fenêtre), et basée sur un concept quelque peu différent du concept de fréquence: le concept d'échelle. Au lieu de considérer des fonctions oscillantes placées à l'intérieur d'une fenêtre, que l'on fait ensuite coulisser le long d'un signal à analyser (les Gaborettes), les ondelettes sont davantage des copies les unes des autres, copies presque conformes puisqu'elles sont de forme constante et ne diffèrent que par leur taille. La décomposition (continue) en ondelettes est similaire à la décomposition de Gabor: un signal s'écrit sous la forme d'une superposition de telles ondelettes décalées et dilatées. Les poids de ces ondelettes dans la décomposition (appelés les coefficients d'ondelettes) forment la transformée en ondelettes, qui est donc une fonction de deux variables: le temps et l'échelle (ou dilatation).
Voir encart
pour plus de détails.
Avec l'analyse par ondelettes et l'analyse par Gaborettes, nous disposons donc de deux méthodes de décomposition des signaux en fonctions élémentaires, engendrées par des transformations simples d'une fonction de base. La fonction de base est soit déplacée et modulée (dans le cas des Gaborettes), soit translatée et dilatée (ondelettes). La différence fondamentale entre les deux tient précisément à cette opération de dilatation: les ondelettes s'adaptent d'elles mêmes à la taille des caractéristiques qu'elles recherchent. Elles sont très étendues pour étudier les basses fréquences (les grandes échelles), et très fines pour étudier des phénomènes plus transitoires (hautes fréquences, ou petites échelles). Cette procédure, développée par S. Mallat et systématisée par I. Daubechies, porte le nom de multirésolution, et suggère une interprétation différente de l'analyse par ondelettes, basée sur les idées de lissage, ou d'approximation des fonctions. Pour illustrer notre propos, éloignons-nous pour un temps des exemples de signaux musicaux que nous avons évoqués jusqu'ici, et prenons un exemple de fonction de deux variables particulière, en l'occurence une image. Une image (en noir et blanc pour simplifier) consiste en une série de points (pixels) plus ou moins sombres (on parle de niveaux de gris), que l'on peut idéaliser comme une fonction dans l'espace à deux dimensions (le plan de l'image), qui associe à chaque point un nombre représentant son niveau de gris (l'intensité lumineuse en ce point). Lisser notre image (mathématiquement, en prendre le produit de convolution avec une fonction très régulière) revient à la rendre floue, c'est à dire à en diminuer la résolution. Si nous considérons maintenant deux versions floues de l'image, à des résolutions différentes, nous pouvons nous intéresser aux détails qui sont toujours présents dans l'image la moins floue, mais ont disparu dans l'image la plus floue. Mathématiquement, ceci revient à calculer une différence entre les deux fonctions lissées, et l'on peut montrer que cette opération est identique au calcul d'une transformée en ondelettes (bidimensionnelle) de notre image. A ce moment là, la reconstruction de l'image à partir de ses coefficients en ondelettes prend une signification intuitive évidente: l'image, à sa résolution la plus grande, est égale à la somme d'une version floue, et des détails apparaissant à des échelles différentes, c'est à dire à des résolutions différentes.



Figure 2: les coefficients d'ondelettes vus comme différences
de deux lissages à des résolutions différentes:
en haut: une image à une bonne résolution.
au centre: une version lissée, à une résolution plus faible.
en bas: les coefficients d'ondelettes, différence entre les deux
images précédentes: détails présents dans
la première image et absents de la seconde.
Les décompositions en ondelettes existent dans plusieurs versions, que l'on choisit en fonction de l'application visée. On distingue principalement deux types de décompositions en ondelettes. La première fournit des décompositions non-redondantes, dans lesquelles on les ondelettes considérées sont exactement en ``nombre suffisant║'' pour caractériser la fonction analysée. Les ondelettes correspondantes forment alors une base de l'espace considéré. Ces bases d'ondelettes sont très utilisées, en particulier pour des applications en compression des signaux (voir la section 4 ci dessous). L'alternative consiste à travailler avec des familles surabondantes d'ondelettes. Ce faisant, on augmente bien entendu le nombre de coefficients d'ondelettes considéré, dans l'espoir de renforcer leur significativité. Les décompositions redondantes sont très utilisées en analyse des signaux par exemple.
2. UNE REPRESENTATION EFFICACE
Une partition musicale est une représentation formidablement efficace du signal musical, dans la mesure où elle schématise une énorme quantité d'informations en utilisant relativement peu de signes. La première question qui vienne à l'esprit est de savoir si les décompositions en ondelettes sont capables d'approcher une telle efficacité, ne serait-ce que dans des situations nécessairement idéalisées où le signal est moins complexe. Par exemple, étant donnée une fonction mathématique, ses coefficients d'ondelettes permettent ils de retrouver simplement certaines de ses caractéristiques ? Ou encore, étant donné un signal produit par un phénomène bien déterminé, peut on à l'aide d'une transformée en ondelettes accéder à certaines informations relatives à ce phénomène, ou encore détecter ce phénomène quand il se produit (on peut penser à des applications très pratiques, comme par exemple détecter automatiquement un dysfonctionnement d'un moteur par analyse du bruit qu'il produit)? Il est bien évident que la réponse est négative dans le cas général (l'outil universel n'existe pas...). Ceci étant, les décompositions en ondelettes ont quand même permis de répondre par l'affirmative dans nombre de cas précis. Nous allons en donner quelques exemples.
Une famille d'exemples nous est fournie par les mathématiques, comme l'ont montré Y. Meyer et ses collaborateurs. Une des problématiques traditionnelles de l'analyse mathématique est de caractériser ce que l'on appelle les propriétés de régularité des fonctions. Très grossièrement, la régularité d'une fonction traduit la rapidité avec laquelle elle varie. Plus précisément, les fonctions sont regroupées en classes (appelées espaces fonctionnels) de fonctions possédant toutes certaines propriétés génériques. Certaines de ces propriétés étant souvent difficiles à vérifier directement, il est souvent nécéssaire de les traquer par des moyens détournés. La transformation de Fourier en est un, et les fonctions de certaines classes peuvent être caractérisées par les propriétés de leur transformée de Fourier: en schématisant à l'extrême, plus une fonction f(t) varie rapidement (c'est à dire moins elle est régulière), plus elle contient de sinusoïdes sin(wt) et cos(wt) de fréquences w élevées, et plus sa transformée de Fourier décroît lentement quand la fréquence w augmente. Par malheur, autant cette idée paraît naturelle intuitivement, autant elle est difficile à traduire dans un contexte mathématiquement rigoureux. L'un des apports essentiels de l'analyse par ondelettes dans ce contexte a été de montrer que cette idée simple est bien plus correcte quand on la formule en utilisant des ondelettes quen utilisant des sinusoïdes. Plus une fonction est régulière, plus ses coefficients d'ondelettes décroissent vite quand l'échelle décroît, et vice versa. Bien entendu, tous les espaces fonctionnels ne peuvent être caractérisés aussi simplement. Le résultat est simplement que l'analyse par ondelettes permet d'en ``attraper'' plus que l'analyse de Fourier. Dans un même ordre d'idées, la variable déchelle des ondelettes permet d'analyser finement les propriétés de fonctions ou objets fractals, c'est à dire se reproduisant à l'identique à des échelles différentes. C'est ainsi que l'on a pu mettre en évidence les propriétés fractales de certaines fonctions mathématiques (comme la célèbre fonction de Riemann-Weierstrass), ou encore du signal de vitesse d'un fluide dans un écoulement turbulent.
Cependant, les atouts des décompositions en ondelettes vont bien au delà de ces propriétés mathématiques. En effet, il savère que nombre de fonctions ou signaux que l'on peut rencontrer couramment en pratique, sont efficacement représentés par des ondelettes. Par efficacement, nous entendons que non seulement les coefficients d'ondelettes permettent de ``lire facilement'' les propriétés de ces signaux, mais aussi que cette information est contenue dans un nombre relativement limité de ces coefficients (autrement dit, que seule une petite partie de ces coefficients sont représentatifs, tous les autres étant petits). En plus des applications à la compression de données que nous allons décrire plus en détails un peu plus loin, une telle capacité à ``concentrer'' l'information est souvent un avantage décisif en pratique. Il est en effet bien plus aisé de manipuler un nombre limité de coefficients qu'un grand nombre.

Figure 3: transformée en ondelettes des dix premiers millisecondes d'un son de vibraphone, tracé en haut de la figure (fournie par Ph. Guillemain, LMA, CNRS Marseille). Il s'agit d'une fonction à valeurs complexes, dont on représente le module et l'argument au moyen d'images. L'axe horizontal est l'axe du temps, et l'axe vertical est l'axe des échelles. L'image du haut représente le module de la transformée, et décrit l'importance relative des différents temps et échelles dans le signal. En l'occurrence, après une période transitoire (l'attaque du son), on distingue clairement une échelle prépondérante, caractéristique de la hauteur du son. L'image du bas représente l'argument de la transformée en ondelettes, qui peut être utilisé pour mesurer finement cette hauteur de son.
Pour illustrer davantage les perspectives ouvertes par cette efficacité, l'exemple du débruitage de signaux bruités est extrêmement intéressant. Il s'agit d'un problème rencontré quotidiennement par nombre d'ingénieurs ou de scientifiques à qui se posent des problèmes de mesure. En effet, quand on mesure une quantité physique, disons une température pour fixer les idées, la mesure nest jamais exacte. Le résultat obtenu est entaché d'une erreur, qui provient en général de facteurs multiples comme l'imprécision de l'appareil, les vibrations diverses du milieu où celui-ci se trouve,... On dit alors que le signal obtenu est la somme du vrai signal et d'un bruit de mesure, et le problème qui se pose est souvent de se débarrasser du bruit pour accéder à l'information ``pure''. Il sagit bien entendu d'un problème très classique, qui a reçu beaucoup d'attention et des réponses souvent satisfaisantes. Il est cependant intéressant de décrire la solution très simple qui est donnée par l'analyse par ondelettes. Il savère que très souvent, le signal ``pur'' est représenté efficacement (au sens donné plus haut) par ses coefficients d'ondelettes, alors que le bruit quant à lui ne l'est pas. Ainsi, l'information intéressante est concentrée dans peu de coefficients d'ondelettes significatifs, alors que la contribution du bruit ne l'est pas, et les coefficients d'ondelettes provenant du bruit sont donc significativement plus faibles que ceux du signal utile. Partant de là, il est facile de ``débruiter'': il suffit de calculer la transformée en ondelettes du signal bruité, et de remplacer par zéro les coefficients qui sont trop faibles (c'est à dire plus petits qu'un certain seuil, que l'on peut calculer à l'avance). Ce faisant, on court le risque de remplacer par zéro aussi quelques coefficients provenant du signal utile, mais ces coefficients étant petits, l'erreur ainsi commise est généralement peu importante, et facile à contrôler.
3. DES ALGORITHMES RAPIDES
L'une des raisons essentielles du succès rencontré par les méthodes basées sur la transformation de Fourier tient dans l'existence d'algorithmes rapides de calcul qui lui sont associés (la fameuse FFT). Or, il s'est avéré que les transformations en ondelettes discrètes, pour peu que l'ondelette soit convenablement choisie, sont naturellement associées à des algorithmes qui peuvent être encore plus efficaces que les algorithmes de FFT.
Pour saisir le fonctionnement de ces algorithmes, il nous faut revenir à la multirésolution que nous avons brièvement évoquée plus haut. Nous limitons notre discussion au cas de transformations en ondelettes dites dyadiques, c'est à dire conservant une certaine redondance. Nous évoquerons le cas des décompositions en bases d'ondelettes un peu plus loin. Les coefficients d'ondelettes d'un signal sont obtenus à partir d'une série de lissages du signal, à des résolutions de plus en plus grossières. La remarque clé (faite initialement dans un contexte de codage du signal de parole, puis en traitement d'images) est que ces lissages peuvent être effectués de façon récursive, en utilisant de façon systématique un unique opérateur de lissage, que nous notons H. H transforme une suite de nombres en une autre suite, lissée. Plus précisément, partant d'un signal échantillonné, c'est à dire d'une série de N nombres
f = {f1, f2,... fN},
que l'on assimile au lissage de notre signal à l'échelle la plus fine considérée:
s0 = f, sa transformée en ondelettes dyadique lui associe une suite de N log(N) coefficients. On calcule tout dabord
s1 = H.s0, puis
s2 = H.s1,
s3 = H.s2,
et ainsi de suite, jusquà l'échelle la plus grande. On montre que les coefficients d'ondelettes eux aussi s'obtiennent suivant une règle similaire, en utilisant un autre opérateur que nous noterons
G: d1 = G.s0, puis
d2 = G.s1,
d3 = G.s2,...

Figure 4:Schématisation d'un algorithme rapide de décomposition en ondelettes: utilisation répétée d'opérateurs de lissage.
Voir
encart pour plus de détails.
Le fait d'effectuer des opérations identiques à toutes les résolutions est en lui même remarquable, si l'on songe que le but de cet algorithmes est de manipuler des ondelettes dont la taille croît proportionnellement à l'échelle. Ceci devrait logiquement se traduire par des coûts en temps de calcul de plus en plus élevés quand l'échelle devient grande. Or, il n'en est rien. Il est facile de démontrer que le nombre d'opérations élémentaires (additions et multiplications) effectuées par les opérateurs H et G ci-dessus est proportionnel à N, le nombre d'échantillons du signal de départ. Comme le nombre déchelles est proportionnel au logarithme de N (ceci résulte du fait que les échelles sont en progression géométrique, et de ce que l'échelle maximale à considérer ne peut être supérieure à la longueur du signal), nous aboutissons à un nombre d'opérations élémentaires proportionnel à N log(N). On dit que l'on a un algorithme de complexité N log(N).
Des considérations tout à fait similaires conduisent à des algorithmes efficaces de reconstruction d'un signal à partir de ses coefficients d'ondelettes, eux aussi de complexité N log(N). Ces algorithmes font eux aussi appel aux mêmes opérateurs G et H.
Dans le cas d'une transformation en ondelettes sans redondance, le nombre de coefficients d'ondelettes calculés est alors égal à N exactement. La procédure est strictement la même que plus haut à ceci près que les opérateurs H et G sont légèrement différents (en fait un peu plus simples), et que le nombre d'opérations qu'ils effectuent est maintenant fonction décroissante de l'échelle (en fait inversement proportionnel à l'échelle). De là, on montre que les algorithmes correspondants de décomposition en base d'ondelettes et de reconstruction sont de complexité N (au lieu de N log(N) comme précédemment).
4.
UNE APPLICATION SPECTACULAIRE: LA COMPRESSION DE DONNEES
La compression de données est l'un des défis majeurs jetés aux mathématiciens d'aujourd'hui. Le développement de ce que l'on qualifie parfois de société de l'information rend nécessaire le stockage et la transmission ultrarapide de quantités gigantesques d'informations de toutes sortes. Le défi est tout d'abord technologique, dans la mesure où il s'agit de stocker un maximum de données dans un volume aussi réduit que possible, ou encore de transmettre un maximum de données de façon aussi économique que possible. Mais le problème se pose aussi en amont, au niveau des mathématiques. En effet, si les mathématiques permettent de réduire la quantité de nombres nécessaires pour coder de telles informations, cela se traduit presque automatiquement par une augmentation des performances tant au niveau du stockage qu'au niveau de la transmission. Encore faut il pour cela que cette réduction puisse être faite rapidement, afin de ne pas pénaliser l'ensemble du processus de transmission.
La technologie numérique actuelle est basée sur ce que l'on appelle la théorie de l'échantillonnage. Cette théorie nous enseigne tout d'abord qu'il est impossible de reproduire sans distorsion un signal continu à partir d'un nombre fini d'échantillons. Plus précisément, le taux auquel l'on échantillonne le signal (c'est à dire le nombre de valeurs par seconde) limite la bande passante, c'est à dire le domaine des fréquences qui sont transmises sans distorsion. La téléphonie actuelle est basée sur ce principe, et fournit une bande passante limitée à 4 kHz environ, très loin en deçà des limites perceptibles par notre oreille. Pour améliorer ces performances, on peut d'une part améliorer la bande passante. Une solution alternative (ou plutôt complémentaire) consiste à représenter différement l'information avant de la transmettre.
Si nous poursuivons avec l'exemple d'un signal sonore, on s'aperçoit assez facilement que des valeurs consécutives de ce signal sont généralement très corrélées: il est souvent possible à partir d'un certain nombre de ces valeurs d'en prédire d'autres, et ce avec une précision acceptable. Ceci démontre que l'information contenue dans les valeurs est redondante, et n'est pas totalement nécessaire pour caractériser le signal. Pour améliorer la qualité du signal, il importe donc de se débarasser de cette redondance. Ceci peut être fait par des méthodes appropriées, dont le prototype est connu sous le nom de méthode de Karhunen-Loève. Le principe essentiel de la méthode de Karhunen-Loève est d'analyser les corrélations présentes dans le signal, et den déduire une autre représentation dans laquelle tous les coefficients sont décorrélés. Le corollaire est qu'une certaine quantité de ces coefficients décorrélés seront nuls ou très petits, et peuvent donc être ``oubliés''. En négligeant ces coefficients, on procède de facto à une compression de données, dans la mesure où l'on représente la même quantité d'informations en utilisant moins de nombres. Et au prix où sont les nombres...
Cependant, les méthodes utilisant les décompositions de Karhunen-Loève souffrent de multiples désavantages. Le principal dentre eux est qu'il sagit de méthodes généralement très difficiles à mettre en oeuvre efficacement, car elles sont peu compatibles avec des algorithmes rapides. C'est pour cela que l'on s'oriente plutôt vers des méthodes plus simples, en espérant qu'elles permettent d'approcher les performances des méthodes optimales, voire même de les surpasser dans certains cas spécifiques. C'est là qu'intervient l'efficacité de la transformation en ondelettes que nous avons mentionnée plus haut. Comme nous l'avons signalé, bon nombre de signaux que l'on rencontre couramment sont efficacement représentés par des ondelettes. C'est en particulier le cas des images, et il est facile d'en comprendre la raison. La raison essentielle tient à la nature même des images. La majeure partie des informations à laquelle nous sommes sensibles se trouve dans ce que l'on appelle les contours de l'image: par exemple les bords des objets, des visages,... qui sont représentés. Les contours sont des régions où l'intensité de l'image varie brutalement, et les coefficients d'ondelettes correspondants sont significatifs, y compris aux petites échelles. Or, une image contient généralement relativement peu de contours, et est régulière (lentement variable) sauf au voisinage des contours. Par conséquent, beaucoup de coefficients d'ondelettes sont faibles (surtout aux petites échelles), et peuvent être négligés sans que cela entraine de distorsion visible sur l'image.


Figure 5: Compression par ondelettes de la première
image de la figure 3: un certain pourcentage des coefficients d'ondelettes
est "oublié" (images effectuées à l'aide d'un
logiciel dû à G. Davis, Université de Dartmouth).
En haut: 90% des coefficients sont oubliés;
l'image est faiblement modifiée.
En bas: 97% des coefficients sont oubliés; l'image est modifiée
de façon plus importante,en particulier sa "texture" (celle
des toits par exemple)
La compression des images est un thème de recherches très actives à l'heure actuelle, car il va bientôt s'agir de définir ce qui sera la méthode de codage des images dans les média et multimédia des années à venir. Les méthodes basées sur les décompositions en ondelettes font partie des méthodes les plus performantes actuellement, et seront peut être le standard de demain. D'ores et déjà, la compression par ondelettes a été adoptée par le FBI pour le stockage des empreintes digitales des citoyens américains.
5. AU DELA DES ONDELETTES
En dépit du grand nombre de succès qu'elle a pu rencontrer et de la diversité des applications qu'elle a trouvées, l'analyse par ondelettes est loin de nous donner une réponse universelle et finale au problème de représentation et codage des signaux. Cependant, elle fournit souvent une réponse qui n'est pas très éloignée de la réponse optimale, ce qui, combiné à la grande simplicité de l'outil et sa grande efficacité algorithmique, explique son succès grandissant. En revanche, dans certains cas bien précis, il est nécessaire de rechercher des techniques permettant de s'approcher plus encore de l'optimalité, tout en essayant de conserver les atouts des ondelettes.
Une approche possible consiste à rechercher des décompositions en ondelettes généralisées. La motivation peut se résumer comme suit. Les ondelettes peuvent être vues comme un ensemble de signaux élémentaires, suffisant pour exprimer n'importe quel signal. En d'autres termes, elles fournissent un dictionnaire de signaux élémentaires, à partir duquel l'on peut reconstruire tout signal. L'analogie avec un dictionnaire est intéressante dès lors que l'on réalise que plus un dictionnaire est complet, plus les phrases qu'il permet de former peuvent être courtes. En effet, plus nous avons de mots à notre disposition, plus il nous sera facile de nous exprimer avec concision. La transcription mathématique de cette idée nous conduit tout droit à la problématique des décompositions adaptatives des signaux. R. Coifman, Y. Meyer et leurs collaborateurs ont montré que les algorithmes rapides associés aux décompositions en ondelettes permettent aussi de définir des ondelettes généralisées (appelés des paquets d'ondelettes), qui offrent une souplesse supplémentaire. Les paquets d'ondelettes contiennent non seulement les ondelettes usuelles, mais aussi une multitude dautre méthodes, toutes aussi efficaces algorithmiquement. Ceci suggère de rechercher, pour un signal donné, laquelle de ces méthode conduit à la représentation la plus efficace, dans un sens donné. Par exemple, si l'application est la compression des signaux, l'on va rechercher la méthode qui fournit une compression optimale. Cette méthodologie est actuellement à létude par les grandes compagnies pétrolières pour la compression des signaux récoltés lors des campagnes de mesure en prospection pétrolière.
Un autre aspect de ce problème concerne le couplage des décompositions en ondelettes avec d'autres méthodes. Si nous prenons encore une fois l'exemple de la compression de données, il faut réaliser que la compression ne se limite pas à trouver une bonne représentation du signal. Il faut aussi se poser le problème du codage des coefficients (pratiquement, les coefficients sont des nombres réels, que l'on code par des suites de zéros et de uns). L'un des problèmes posé à l'heure actuelle est de ``marier'' les méthodes de codage et les méthodes de transformation en ondelettes ou en ondelettes généralisées.
Il est aussi souvent important de se préoccuper de problèmes autres que les problèmes mathématiques, et de faire intervenir par exemple des informations sur la nature même des signaux étrudiés. Si nous considérons par exemple le problème de la représentation économique des sons, il serait illusoire de penser que l'on peut approcher l'optimalité sans se préoccuper du processus physique d'audition. Les psychophysiciens savent depuis longtemps que notre appareil auditif est un outil très sophistiqué, qui a en particulier la capacité de masquer les sons. Par exemple, si nous écoutons un son d'une certaine hauteur (c'est à dire une certaine fréquence), accompagné d'un autre son d'une fréquence proche, d'intensité légèrement plus faible, nous ne percevrons que le premier des deux, le second étant masqué par le premier. C'est ainsi que l'on peut reformuler le problème de codage du son: codons le son avec un minimum de données, tout en nous assurant que la distorsion, c'est à dire l'erreur, sera toujours masquée, et donc jamais entendue. Il existe des méthodes de codage de signaux audiophoniques mettant en oeuvre ces techniques: il sagit maintenant de remplacer par zéro (et donc d'oublier) tous les coefficients d'ondelettes dont on estime qu'ils proviennent d'une partie masquée du signal. Les résultats obtenus jusquà présent par cette technique sont compétitifs par rapport aux méthodes utilisées dans les codeurs commerciaux (pour les minidisques par exemple), mais il y a fort à parier que des progrès seront effectués rapidement.
B. Torrésani <Bruno.Torresani@cmi.univ-mrs.fr>
Last modified: Mon Aug 27 10:00:37 MEST 2001