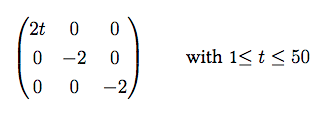A computer-based algorithmic approach to the study of automorphism groups, orbits of smooth rational curves, unirationality and projective models of K3 surfaces

Cédric Mazet
I2M, Aix-Marseille Université
https://cedricmazet.com/

Date(s) : 30/06/2022 iCal
14h30 - 16h30

Une approche algorithmique informatisée de l’étude des groupes d’automorphisme, des orbites de courbes rationnelles lisses, de l’unirationalité et des modèles projectifs de surfaces K3
sous la direction du Professeur Xavier Roulleau.

A computer-based algorithmic approach to the study of automorphism groups, orbits of smooth rational curves, unirationality and projective models of K3 surfaces (thesis)

Abstract: The initial aim of this thesis consisted in determining automorphism groups and upper bounds on the number of orbits of smooth rational curves on surfaces in the family of K3 surfaces having a Néron-Severi group isomorphic to the lattice with Gram matrix

with respect to a xed basis.

To this end, we put computer science at the service of pure mathematics and implemented various computer-based algorithmic solutions that take advantage of a wide array of tools and modern techniques. These solutions not only enabled us to perform a complete study of the family of K3 surfaces mentioned above by determining projective models, computing automorphism groups, studying the orbits of smooth rational curves and discussing the unirationality of their moduli spaces, hence enabling us to provide results far exceeding the objectives which had been set for this thesis, but also turn out to have a framework of application which goes far beyond the family of surfaces mentioned earlier. From the outset of this thesis, we indeed had in mind to develop solutions with a broad scope of application. This endeavor resulted in the production of many computer-based solutions for the study of K3 surfaces, which will hopefully open up new perspectives and help popularize even more the eld of study of K3 surfaces. Please note that all programs produced during this thesis are released in public access: All computer-based solutions produced during this thesis are detailed and available for download on K3surfaces.com.

Keywords: K3, Sage, Magma, automorphisms, smooth rational curves, K3surfaces.com, K3SU.com

Composition du Jury

Frédéric MANGOLTE Aix-Marseille Université	Président du Jury
Xavier ROULLEAU Aix-Marseille Université	Directeur de thèse
Alice GARBAGNATI Università Statale di Milano	Rapporteuse
Davide VENIANI Stuttgart University	Rapporteur
Alessandra SARTI Université de Poitiers	Examinatrice
Pierre LAIREZ École Polytechnique	Examinateur