Inversion de la divergence et systèmes de Hodge dans les espaces de Sobolev critiques
Date(s) : 02/10/2023 iCal
10h30 - 11h30
Soient d ≥ 2, Ω ⊂ ℝd un domaine borné régulier et f ∈ Ld(Ω) avec ∫ Ωf (x)dx = 0. Bourgain et Brezis ont montré l’existence d’un champ de vecteurs X ∈ W01,d(Ω) ∩L∞(Ω) tel que div X = f et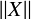 
W1,d + 
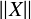L∞ ≲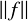
Ld(Ω). On présentera plusieurs extensions de ce résultat, en faisant notamment le lien avec un problème d’approximation dans des espaces de Sobolev critiques. Les résultats présentés ont été obtenus en collaboration avec P. Bousquet, E. Curca, P. Mironescu, L. Moonens, T. Picon, Y. Wang et P. L. Yung.
[su_spacer size= »10″]
Séminaire Analyse et Géométrie
Emplacement
I2M Chateau-Gombert - CMI, Salle de Séminaire R164 (1er étage)
Catégories
