Évènement

Date(s) : 15/05/2023   iCal
11h15 - 12h15

Étant donné un ensemble de directions Ω dans le plan euclidien, on définit l’opérateur maximal directionnel associé M_Ω par:

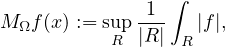
où la borne supérieure est calculée sur l’ensemble des rectangles du plan contenant x, orientés dans une direction de Ω. Un théorème de M. Bateman (2009) assure que, selon la géométrie de Ω, M_Ω est soit borné dans L^p pour tout p > 1, soit non borné dans L^p pour tout p > 1. Nous discuterons comment ce critère peut être appliqué en pratique dans des exemples d’ensembles de directions concrets $Omega$. Il s’agit de résultats en collaboration avec E. D’Aniello et A. Gauvan.

[su_spacer size= »10″]

Séminaire Analyse et Géométrie

Emplacement
I2M Chateau-Gombert - CMI, Salle de Séminaire R164 (1er étage)

Catégories

• Séminaire