Supplementary informations for the article



Time-Frequency Jigsaw Puzzle:

Adaptive multiwindow and multilayered Gabor expansions


Florent Jaillet and Bruno Torrésani





Abstract

We describe a new adaptive family of multiwindow Gabor expansions, which adapt dynamically the windows to the signal's features in time-frequency space. The adaptation is based upon local time-frequency sparsity criteria, and also yields as by-product an expansion of the signal into layers corresponding to different windows.
As an illustration, we show that using simply two different windows with different sizes leads to decompositions of audio signals into transient and tonal layers.


Keywords

Gabor expansion, multiwindow, time-frequency concentration, adaptivity, sparsity, entropy.

EDICS:  2-TIFR - Non-stationary Signals, Time-Frequency and Frequency-Frequency Analysis

pdf file of the paper


Summary:

Principles of the TFJP algorithms
Example of the Glockenspiel signal (TFJP1)
Example of speech signal (TFJP1b)
Comparison between TFJP1 and TFJP2


Principles of the TFJP algorithms:


The main ideas of the TFJP algorithms is to first pave the time-frequency plane with super-tiles, and look within each super-tile for the optimal Gabor representation for the corresponding "piece" of the signal. The decision is taken by associating with each super-tile and each considered Gabor representation an entropy, which measures a local (in the time-frequency domain) sparsity.
Using these reduced multiple Gabor systems, a first approximation of the signal is reconstructed, and the method is recursively applied to the remainders. Different strategies for the decision and the reconstruction may be chosen, that lead to different versions of the algorithm (termed TFJP1, TFJP2 and TFJP1b).
Partial reconstructions (termed layers) from the considered Gabor systems may also be obtained.
Details of the methods can be found in the article. The numerical illustrations below use these versions, starting from two Gabor representations (Gabor frames), using respectively a wide and a narrow copy of the same window (a Gaussian window).



Example of the Glockenspiel signal:

The glockenspiel signal below was decomposed using the TFJP2 algorithm, and the corresponding tonal and transient layers were reconstructed separately.

original signal     glockenspiel signal
tonal layer           glockenspiel: tonal layer
transient layer    transient layer


Other signals used for illustration in the article: Noise, SinDir; speech.



Example of the short piece of speech signal:

This example was generated using the variant TFJP1b of the algorithm, which decomposes the signal into three layers: the tonal layer, i.e.  the component of the signal that is sparsely represented by a Gabor system with wide windows, the transient layer, i.e. the component that is sparsely represented by a Gabor system with narrow windows, and the residual layer, i.e. the component that is not significantly sparsely represented by either the two systems.
Speech 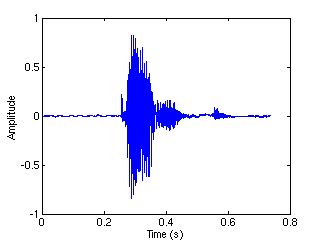     speech        Tonal   speech tonal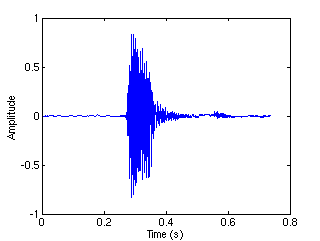
Transient  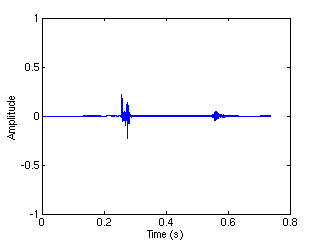 Speech transient    Residual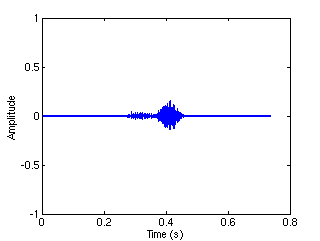  speech residual


Comparison of the time-frequency representations obtained with TFJP1 and TFJP2:

In TFJP1, the super-tiles corresponding to the two windows are selected at the same time, and the corresponding signal components are also reconstructed simultaneously. In TFJP2, a first set of super-tiles (corresponding to the first Gabor system) is estimated and the corresponding component of the signal is reconstructed; then the second set of super-tiles (corresponding to the second Gabor system) is selected from the residual, and the corresponding component of the signal is reconstructed. The procedure is then iterated until the precision is satisfactory. TFJP2 suffers from smaller "interferences" between the two components.

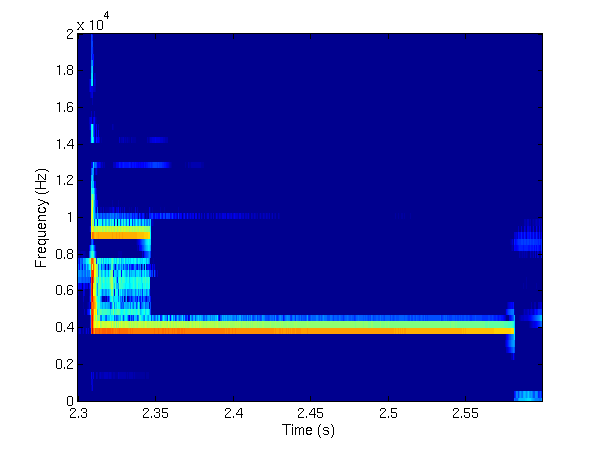
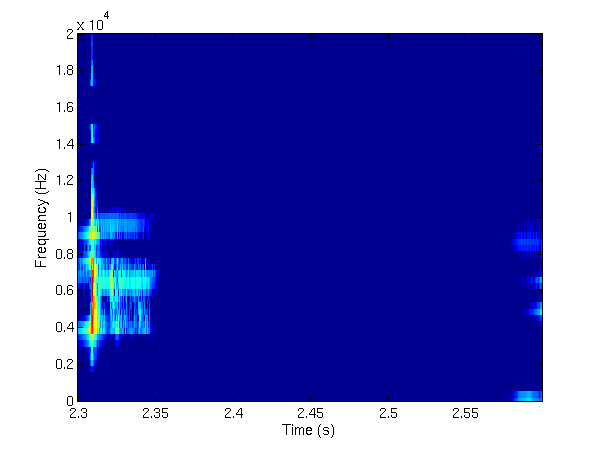
TFJP1 and TFJP2 were run on the same signal, namely the Glockenspiel signal (Glock, see the examples above). Below are displayed the time-frequency representations of the "transient layer" obtained using TFJP1 and TFJP2 respectively. As may be seen from the two time-frequency images, TFJP1 couldn't avoid selecting one of the harmonic components of the signal, while TFJP2 was more precise from this point of view.

TFJP1   TFJP1


TFJP2  TFJP2