suivant: Interpolation linéaire par morceaux monter: Interpolation précédent: Interpolation
Un théorème permet de préciser les conditions de cette interpolation.
Théorème Si les absisses de l'échantillon (1) sont deux à deux distinctes, il existe un unique polynôme p de degré n vérifiant (2). Ce polynôme est de la forme
En matlab, le calcul de ce polynôme peut s'effectuer avec la commande polyfit. Le polynôme peut ensuite être évalué avec la commande polyval. Voici un exemple d'utilisation de ces commandes :
%Définition d'un échantillon
n=4;
x=sort(rand(1,n+1));
y=randn(1,n+1);
%Calcul du polynome d'interpolation
p=polyfit(x,y,n);
%Evaluation du polynome sur [0 1]
t=linspace(0,1,100);
yt=polyval(p,t);
%Affichage
plot(x,y,'ro',t,yt,'b-');
xlabel('x')
ylabel('y')
h=legend('échantillon','interpolation');
Le théorème suivant l'ordre de l'erreur que l'on commet en interpolant une fonction f fixée par un polynome
Théorème Soient f une fonction continûment dérivable à l'ordre n+1 sur un intervalle I et un échantillon de f sur I
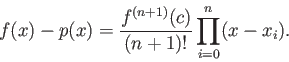
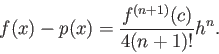
Frederic Richard, Aix-Marseille University, 2015