Interpolation

L'interpolation est un procédé mathématique qui permet d'étendre la définition d'une fonction d'un ensemble fini de points à un ensemble quelconque de points. Disposant d'un échantillon

$$(x_i,y_i), i=0,\cdots,n,$$

on cherche une fonction 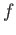$f$ telle que

$$f(x_i)=y_i, i=0,\cdots,n.$$

La fonction f est recherchée au sein d'une famille de fonctions (polynomes d'ordre m, polynomes par morceaux,...). La famille choisie dépend des hypothèses que l'on fait sur la fonction sous-jacente à l'échantillon (continuité, dérivabilité,...). On distingue plusieurs types d'interpolation selon les familles de fonctions. Dans ce chapitre, nous verrons plusieurs types d'interpolation :

• interpolation polynomiale,
• interpolation polynomiale par morceaux,
• interpolation trigonométrique,
• interpolation spline.