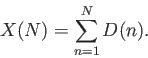Exercice 2 (marche aléatoire)

On s'intéresse à la simulation de la trajectoire d'un promeneur imaginaire qui à chaque pas n avance d'une longueur vers la droite avec probabilité p ou vers la gauche avec probabilité q=1-p. On note D(n) la variable décrivant le nème pas effectué (D(n)=-1 si le pas est à gauche et D(n)=1 si à droite). On définit

$$X(N) = \sum_{n=1}^N D(n).$$

Le point (X(N),N) donne la position du marcheur après N pas effectués en partant de (0,0).

1. Écrire une fonction Promeneur qui calcule la position du promeneur après N pas et représente de manière optionnelle la trajectoire depuis le premier pas.
2. Lancer M fois la fonction Promeneur pour une valeur de N donnée (M»N) en retenant les positions X(N).
3. Calculer la moyenne et l'écart-type des positions retenues, éventuellement en utilisant les commandes mean et std.
4. Tracer l'histogramme de ces positions à l'aide de la commande hist.
5. Interpréter ces résultats à l'aide du théorème centrale limite. Superposer à l'histogramme la distribution limite prédite par TCL.