suivant: À propos de ce monter: . précédent: Exercice 5 (Polynôme de
Les B-splines sont des fonctions qui servent pour la représentation de courbes et sont très utilisées pour l'approximation. Elles peuvent se définir d'une manière itérative.
On fixe un entier n et un ensemble ordonné de n+2 réels distincts (appelés n![]() uds)
uds)
![\begin{displaymath}\forall \: i \in [\![0,n]\!], \: B_i^0(u) = \left\{\begin{arr...
...u \in [a_i,a_{i+1}[, 0 & \mathrm{sinon} \end{array} \right. \end{displaymath}](img11.png)
Les B-splines d'ordre j sont des polynômes d'ordre j par morceaux entre les n![]() uds successifs et continûment dérivables à l'ordre j-1 pour j>0. Pour j>1, la dérivée d'une B-spline d'ordre j vaut
uds successifs et continûment dérivables à l'ordre j-1 pour j>0. Pour j>1, la dérivée d'une B-spline d'ordre j vaut
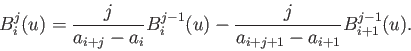
Frederic Richard, Aix-Marseille University, 2015