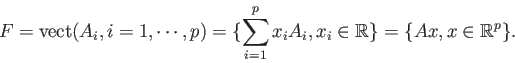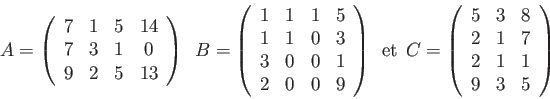Exercice 1

Soit

$$A=(A_1 \vert \cdots \vert A_p), \:\:\: \mathrm{avec} \:\: A_i \in \mathbb{R}^n$$

une matrice formée par concaténation de p vecteurs de taille n. On considère le sous-espace vectoriel F

$$F=\mathrm{vect}(A_i, i=1,\cdots,p)=\{\sum_{i=1}^p x_i A_i,x_i \in \mathbb{R} \}=\{Ax,x \in \mathbb{R}^p \}.$$

On s'intéresse au calcul de la projection orthogonale d'un vecteur b de taille n sur F, càd du vecteur qui réalise sur F le minimum de

$$J(v) = \Vert v -b \Vert^2$$

L'algorithme proposé est le suivant :

1. On calcule une base orthonormée B de F.
2. On obtient le résultat en projetant y dans B.

Mettre en uvre cet algorithme sous la forme d'une fonction qui retourne la projection orthogonale et la dimension de l'espace F.

Tester cette fonction sur des matrices bien choisies et l'appliquer aux matrices

$$A = \left( \begin{array}{cccc} \par 7 & 1 & 5 & 14 \\ 7 &... ... 2 & 1 & 7\\ 2 & 1 & 1\\ 9 & 3 & 5 \end{array}\right)$$