Séminaire des doctorants de Saint-Charles
Responsables
Fréquence
Hebdomadaire
Jour-Horaires
Mercredi 10h30
Lieu
St Charles, FRUMAM (comment y accéder ?)
Contacts
joffrey.mathien_at_univ-amu.fr,
thomas.harbreteau_at_univ-amu.fr,
Ce séminaire, en activité depuis octobre 2021, se propose de réunir informellement toutes les semaines les doctorant⋅e⋅s de l’I2M. L’objectif est de présenter sur des thèmes qui nous intéressent, liés ou pas à nos thèses, et bien entendu d’apprendre à mieux nous connaître entre doctorants Marseillais. Nous invitons également régulièrement des orateurs extérieurs à l’université.
Nous sommes ouverts à toutes les thématiques de recherche et la seule condition est de rendre les exposés le plus accessible possible à tous. (un bon guide pour cela : http://www.ams.org/profession/leaders/workshops/gcoll.pdf)
À bientôt !!!
Pour s’inscrire à la liste de diffusion, cliquez ici.
Si cela ne fonctionne pas, ou si vous avez des questions, n’hésitez pas à nous écrire.
Historique des responsables :
– Octobre 2021 – Août 2023 : Yenni Cherik, Naoufal Bouchareb, Magali Jay.
– Septembre 2023 – Juillet 2024 : Joffrey Mathien.
Les prochains séminaires
Pas d'évènements à afficher
Événements passés
03
Mai
Le concept de b-frames l’opérateur b-adjoint
(...)
Le concept des b-frames est un concept qui généralise les frames pour les espaces de Hilbert. En considérant une suite dans un espace de Banach [...]
26
Avr
La théorie de Thurston dans la dynamique holomorphe
(...)
Cet exposé sera autour du théorème de caractérisation de Thurston, qui était démontré par le médaillé de Fields William Thurston dans les années quatre-vingt. En [...]
12
Avr
Introduction à l’homologie cyclique
(...)
On commencera par parler d’homologie en général, par ce qui me semble être les différentes approches « historique » qui ont conduit à l’émergence de [...]
05
Avr
Une introduction à la notion de courants géodésiques
(...)
Les courants géodésiques ont été introduits en 1986 par Bonahon dans le but d'étudier les 3-variétés. Depuis lors, ils ont eu de nombreuses applications en [...]
31
Mar
Surfaces à bord polygonal dans l’espace pseudo-hyperbolique
(...)
Dans un récent papier de Labourie, Toulisse et Wolf (Plateau Problems for Maximal Surfaces in Pseudo-Hyperbolic Spaces) résolvent le problème de Plateau pour un type [...]
Théorème de Cartan-von Neumann
Yenni Cherik (I2M, Aix-Marseille Université)
Le théorème de cartan-Von neumann dit qu'un sous groupe fermé de GL(n,R) est une sous variété de M(n,R)=R^{n^2}. Nous allons rappeler ce qu'est une sous [...]
Un lien fondamental entre la mécanique des fluides, l'analyse de Fourier et la cohomologie.
Anatole Gaudin (I2M, Aix Marseille université)
La décomposition de Hodge est un outil important de la géométrie différentielle qui permet de relier certaines propriétés topologiques de variétés lisse avec des propriétés algébrique [...]
Trajectoires dans des pavages
Magali Jay (I2M, Aix Marseille université)
Le but de cet exposé est de présenter les "tiling billiards" (billards dans des pavages). Imaginons deux matériaux d'indice optique opposés (certains matériaux ont un [...]
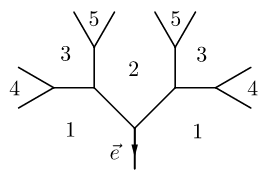
Action de groupe sur les arbres 2
Ulysse Remfort (I2M, Aix-Marseille Université)
Après avoir donné toutes les définitions nécessaires, l’un des buts de cet exposé sera de comprendre et démontrer le théorème suivant dû à Jean-Pierre Serre [...]
Action de groupe sur les arbres
Ulysse Remfort (I2M, Aix Marseille université )
Après avoir donné toutes les définitions nécessaires, l'un des buts de cet exposé sera de comprendre et démontrer le théorème suivant dû à Jean-Pierre Serre [...]
Polytope Extensions with Small Diameter
Kirill Kukharenko (Université de Magdeburg)
Bounding the combinatorial diameter of a polytope is a well-known and long-standing open problem. The great theoretical and practical interest in this question originates from [...]
Les groupes auto-similaires contractants
Nikolai Prochorov (I2M, Aix-Marseille Université)
La théorie de groupes auto-similaires relie d'une belle manière différents domaines de mathématiques, par exemple, topologie, combinatoire, systèmes dynamiques et la théorie géométrique des groupes. [...]
18
Nov
L'analyse harmonique pour tous
(...)
La présentation sera une sorte de cours d'introduction à l'analyse harmonique. Le but premier est de donner l'intuition derrière cette théorie qui tourne autour de [...]
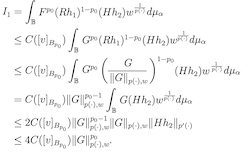
Inégalités à poids variable pour le projecteur de Bergman
Brice Zotsa (I2M, Aix-Marseille Université)
TBA
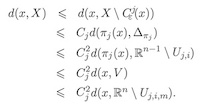
Bilipschitz triviality in o-minimal structures
M'hammed Oudrane (LJAD, Université de Nice)
Hardt’s triviality states that a definable family of sets is generically definably topologically trivial. In this talk we will focus around the metric counterpart of [...]
Parlementons !
Lucie Devey (Université Grenoble-Alpes)
Soit X une variété torique* projective et lisse (ex: un produit d'espaces projectifs P^d1x ... x P^dr). A tout fibré équivariant E sur X, on [...]
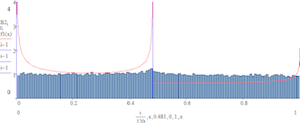
Distribution modulo 1
Juan Marshall (école polytechnique de paris, centre mathématique Laurent Schwartz.)
Dans cet exposé on discutera des résultats métriques sur la distribution modulo 1 des suites de puissances et aussi de problèmes liés comme la régularité [...]
28
Sep
Fractions continues sur les groupes de Hecke.
Julien Boulanger (Université Grenoble-Alpes)
Dans cet exposé on s'intéressera aux groupes de Hecke, qui peuvent être vus comme une généralisation du groupe PSL(2,Z), et qui sont des groupes fuchsiens. [...]
Géometrie interne des fibrations de Milnor
Yenni Cherik (I2M, Aix-Marseille Université)
Soit f : (C²,0) → (C,0) un polynôme de deux variables complexes tel que la courbe complexe d’équation f(x,y) = 0 ait une singularité isolée [...]
