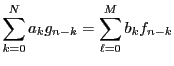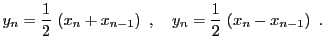La fonction conv permet d'effectuer un filtrage
FIR (attention aux effets de bord: la longueur du signal filtré
est différente de celle du signal original).
La fonction filter permet de mettre en œuvre un filtrage
FIR ou IIR par filtrage récursif. Par exemple
g = filter(b,a,f)
retourne la solution 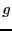 de l'équation récursive
de l'équation récursive
Le choix 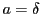 donne un filtrage FIR, c'est à dire un
filtrage de convolution avec la suite finie
donne un filtrage FIR, c'est à dire un
filtrage de convolution avec la suite finie 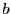 . On peut en voir deux exemples
dans la figure 2, pour des suites
. On peut en voir deux exemples
dans la figure 2, pour des suites 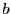 constantes de longueur 1 et 10
respectivement.
constantes de longueur 1 et 10
respectivement.
Figure 2:
Deux exemples de filtrage passe-bas effectués avec la fonction filter: 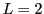 et
et 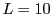 .
.
|
|
- En utilisant la fonction randn, générer un signal pseudo-aléatoire de
longueur donnée (par exemple, 256 ou 512);
le représenter graphiquement, ainsi que son spectre (module carré de sa
transformée de Fourier).
- En utilisant la fonction filter, effectuer un filtrage
passe bas et un filtrage passe haut de la forme
(on se persuadera par un calcul simple -i.e. une TFD-, qu'il s'agit bien
de filtres passe-bas et passe-haut).
On représentera sur un graphe le signal et sa version filtrée, et sur un autre
leurs spectres respectifs.
- Même question avec le filtre défini par
Bruno Torresani
2009-02-18