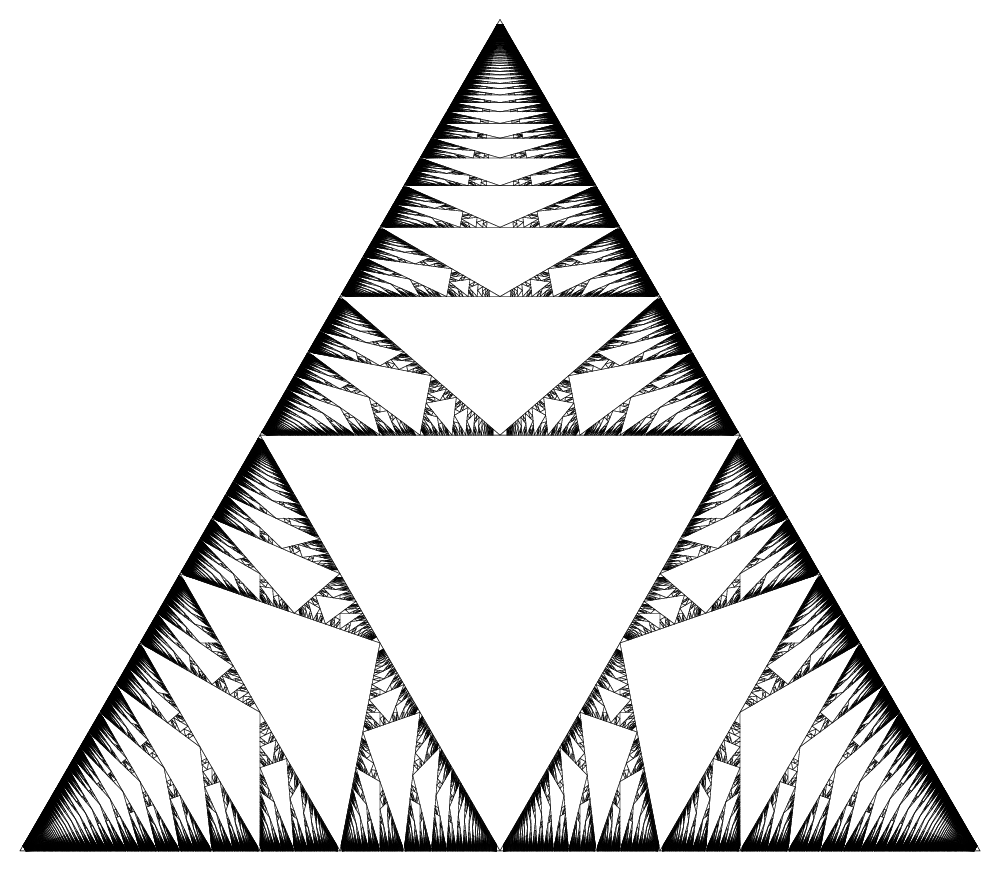
Baderne de Rauzy

Pierre ARNOUX
I2M, Aix-Marseille Université
/user/pierre.arnoux/

Date(s) : 13/05/2022 iCal
11h00 - 12h00

La baderne de Rauzy (Rauzy gasket en anglais) est un sous ensemble fractal du triangle équilatéral qui est apparu plusieurs fois de façon indépendante dans les 40 dernières années dans divers problèmes mathématiques:
–fréquences des lettres dans des mots infinis de faible complexité généralisant les mots de rotation
–ensemble de définition de certains algorithmes généralisant l’algorithme usuel des fractions continues et l’algorithme d’Euclide
–ensemble des paramètres possibles pour des familles de systèmes dynamiques simples stables par une opération d’induction
–ensemble des paramètres pour une famille de pseudo-groupes minimaux
–ensemble des directions de champ magnétique pour lesquelles le mouvement d’un électron soumis à ce champ et bougeant sur une surface triplement périodique admet des orbites infinies

Cet ensemble est homéomorphe, mais pas difféomorphe, à des ensemble fractals classiques, comme le triangle de Sierpinski ou la baderne d’Apollonius.

Dans cet exposé élémentaire, on expliquera d’abord ce qu’est un gasket et une baderne. On donnera ensuite plusieurs définitions simples et équivalentes de la baderne de Rauzy, on montrera les homéomorphismes avec d’autres ensembles classiques, et on expliquera pourquoi sa dimension et sa mesure sont difficiles à calculer.