Exercice 4 (fraction continue)

Une fraction continue est une expression de la forme :

$$q_1 + \frac{1}{q_2+\frac{1}{q_3+\frac{1}{\ddots q_{n-1} + \fr... ...: q_k \in \mathbb{N} \:\: \mathrm{et} \:\: e_n \in \mathbb{R}.$$

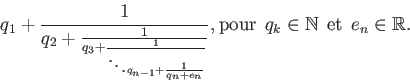
Il est possible de décomposer tout nombre réel x en fraction continue de la manière itérative suivante :

$$e_0 = x \:\:\:\: \mathrm{et} \:\:\:\:\forall \: k=1,\cdots,n, q_k=E(e_{k-1}), e_n=\frac{1}{e_{k-1}-q_k}.$$

A partir de cette décomposition, on peut calculer une série d'approximations rationelles de x dont la précision augmente avec n :

$$\forall \: n>0, f_n = \frac{a_n}{b_n} = q_1 + \frac{1}{q_2+\f... ...frac{1}{q_n}}}}, a_n \in \mathbb{Z}, b_n \in \mathbb{N^\star}.$$

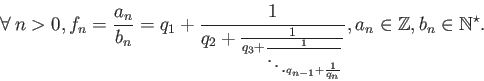
Ces approximations rationnelles s'obtiennent également de manière itérative :

$$\begin{array}{l} a_0=1, b_0= 0, a_1=q_1, b_1=1, \\ \forall k... ...q_k a_{k-1} + a_{k-2}, b_k=q_k b_{k-1} + b_{k-2}. \end{array}$$

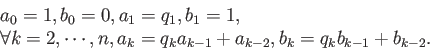
Ecrire un programme qui permet de calculer une approximation rationnelle d'un réel x à une précision donnée en utilisant les fractions continues.