Soit
une famille libre de vecteurs d'un même espace vectoriel E. Le procédé de Gram-Schmidt permet de trouver une base orthonormée du sous-espace vectoriel F engendré par la famille A.
Ce procédé est récursif. A l'initialisation, on définit
Supposons qu'à l'étape k (1<k<n), on dispose d'une base orthonormée
de l'espace engendré par les k premiers vecteurs de A. On définit alors le vecteur
puis le vecteur
La famille
forme alors une base orthonormée de l'espace engendré par les k+1 vecteurs de A.
Mettre en  uvre ce procédé dans une fonction. Utiliser cette dernière pour construire des bases orthonormées de
uvre ce procédé dans une fonction. Utiliser cette dernière pour construire des bases orthonormées de 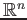 . Pour cela, on pourra générer des familles libres de manière aléatoire comme dans l'exemple ci-dessous
. Pour cela, on pourra générer des familles libres de manière aléatoire comme dans l'exemple ci-dessous
A=floor(800*rand(6,6))
rank(A)
Frédéric Richard, Aix-Marseille Université
2012-12-06
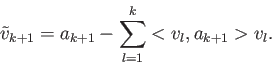
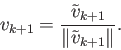
![]() uvre ce procédé dans une fonction. Utiliser cette dernière pour construire des bases orthonormées de
uvre ce procédé dans une fonction. Utiliser cette dernière pour construire des bases orthonormées de ![]() . Pour cela, on pourra générer des familles libres de manière aléatoire comme dans l'exemple ci-dessous
. Pour cela, on pourra générer des familles libres de manière aléatoire comme dans l'exemple ci-dessous