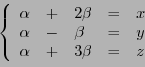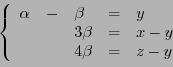Subsections
Espaces vectoriels
La notion d'espace vectoriel est une notion centrale dans de nombreux
problèmes de mathématiques, physique, chimie,....
En effet, la propriété de linéarité
est commune, au moins en première approximation, à beaucoup
de solutions de problèmes simples (problème de
vibration de cordes ou ressorts, de propagation de la
chaleur,...).
On peut résumer la propriété de linéarité de la façon
suivante: si 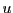 et
et 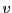 sont deux solutions d'un problème donné, alors
sont deux solutions d'un problème donné, alors 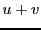 est
solution également, ainsi que
est
solution également, ainsi que 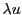 pour tout nombre
(appelé scalaire)
pour tout nombre
(appelé scalaire) 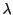 .
.
Le cadre mathématique adapté à ce type de situation est le cadre
des espaces vectoriels, qui est étudié
dans ce chapitre. Les éléments des espaces vectoriels sont
appelés vecteurs, notion qui généralise
les vecteurs rencontrés en géométrie vectorielle.
Pour bien distinguer les différents objets
mathématiques manipulés, on notera dans ce chapitre les vecteurs
avec une flèche (par exemple, 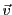 ), notation qu'on oubliera ensuite.
), notation qu'on oubliera ensuite.
On va dans ce chapitre manipuler des objets, et définir des
opérations entre ces objets. Le langage adapté à la
manipulation des objets est celui de la théorie des ensembles, dont
on ébauche ici quelques aspects importants.
Il n'est pas nécessaire d'introduire la notion d'ensemble (qu'on
nomme aussi parfois collection, famille ou regroupement),
constitué d'éléments. Le nombre d'éléments d'un ensemble
est appelé son cardinal. Le cardinal d'un ensemble  est
noté
est
noté
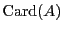 , ou
, ou 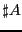 .
.
Une relation importante entre deux ensembles est la relation d'inclusion.
Un ensemble  est inclus dans un ensemble
est inclus dans un ensemble  , relation que l'on note
, relation que l'on note
si tout élément de  est aussi élément de
est aussi élément de  . On note ceci
sous la forme
. On note ceci
sous la forme
 est alors un sous-ensemble de
est alors un sous-ensemble de  .
.
REMARQUE 1.1
Il existe un ensemble remarquable, qui est inclus dans tout ensemble:
l'
ensemble vide, noté
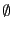
. Tout ensemble

est
également inclus dans lui même. On a donc pour tout ensemble

,
REMARQUE 1.2
Il est fondamental de bien saisir la différence entre les notions
d'appartenance à un ensemble, et d'inclusion dans un ensemble.
Par exemple, le nombre
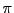
appartient à l'ensemble

des nombres réels, alors que l'ensemble
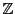
des nombres entiers
est quant à lui inclus dans l'ensemble des nombres réels.
Par contre, le singleton 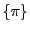 , c'est à dire l'ensemble
constitué de l'unique élément
, c'est à dire l'ensemble
constitué de l'unique élément 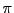 , est un sous-ensemble de
, est un sous-ensemble de
 .
On note cela
.
On note cela
Deux ensembles  et
et  sont égaux si tout élément de
sont égaux si tout élément de  est
élément de
est
élément de  (c'est à dire
(c'est à dire
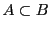 ), et vice versa
(
), et vice versa
(
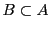 ). Ainsi, on a la propriété fondamentale
). Ainsi, on a la propriété fondamentale
Pour démontrer que deux ensembles sont égaux, on doit donc
démontrer les deux relations d'inclusion, c'est à dire
-
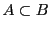 signifie:
signifie:
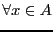 ,
, 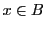 .
.
-
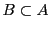 signifie:
signifie:
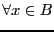 ,
, 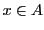 .
.
Etant donnés deux ensembles  et
et  , leur union
, leur union 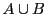 est l'ensemble
formé des éléments de
est l'ensemble
formé des éléments de  et des éléments de
et des éléments de 
Leur intersection est constituée des éléments communs à  et
et  :
:
Les opérations de réunion et d'intersection possèdent un certain nombre
de propriétés importantes, listées ci-dessous. Les démontrer
est un bon exercice. A défaut, on peut s'en convaincre en dessinant
des ``patates'' (qu'on appelle diagrammes de Venn).
Dans ces propriétés, 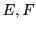 et
et 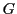 sont des ensembles.
sont des ensembles.
- Union et intersection sont associatives:
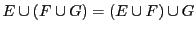 ,
et
,
et
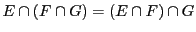 .
.
- Union et intersection sont commutatives:
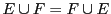 , et
, et
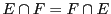 .
.
- Distributivité
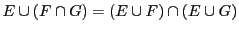 , et
, et
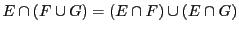 .
.
Etant donnés deux ensembles  et
et  , on a parfois à considérer
l'ensemble des éléments de
, on a parfois à considérer
l'ensemble des éléments de  qui n'appartiennent pas à
qui n'appartiennent pas à  .
Cet ensemble est appelé la différence ``
.
Cet ensemble est appelé la différence `` moins
moins  '', et est noté
'', et est noté
Lorsque  est un sous-ensemble de
est un sous-ensemble de  ,
,
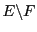 est appellé le complémentaire de
est appellé le complémentaire de  dans
dans  ,
et on le note
,
et on le note
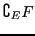 ou encore
ou encore
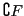 lorsqu'aucune
confusion n'est possible.
lorsqu'aucune
confusion n'est possible.
Finalement, on utilise également la notion de
différence symétrique de deux ensembles  et
et  , notée
, notée
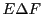 , qui est constituée des éléments de
, qui est constituée des éléments de  n'appartenant
pas à
n'appartenant
pas à  et des éléments de
et des éléments de  n'appartenant pas à
n'appartenant pas à  :
:
Tout d'abord, distinguons les notions de paire et de couple.
Une paire est un ensemble de deux objets. Un couple est lui aussi
formé de deux objets, mais on distingue le premier (appelé
première composante du couple) du second (appelé seconde
composante du couple). Conventionnellement, on note 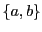 la paire
constituée des objets
la paire
constituée des objets 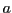 et
et 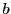 , et
, et 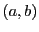 le couple constitué de
ces mêmes objets. On a donc
le couple constitué de
ces mêmes objets. On a donc
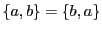 , alors que
, alors que
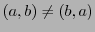 .
.
Etant donnés deux ensembles  et
et  , le produit cartésien de
, le produit cartésien de  et
et  ,
noté
,
noté 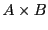 , est l'ensemble des couples dont le premier élément
appartient à
, est l'ensemble des couples dont le premier élément
appartient à  et le second appartient à
et le second appartient à  :
:
Si  et
et  sont deux ensembles finis, de cardinaux respectifs
sont deux ensembles finis, de cardinaux respectifs
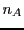 et
et 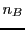 , alors le cardinal de
, alors le cardinal de 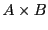 vaut
vaut 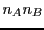 :
:
Etant donnés trois ensembles  ,
,  et
et 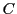 , le produit Cartésien des
ensembles
, le produit Cartésien des
ensembles 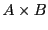 et
et 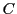 sera noté
sera noté
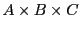 (et pas
(et pas
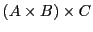 ). Si
). Si 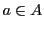 ,
, 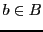 et
et 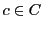 , on notera
, on notera
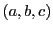 le couple
le couple 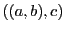 , que l'on appellera triplet.
, que l'on appellera triplet.
On définira similairement les produits Cartésiens de 4 ensembles,
5 ensembles, et ainsi de suite. Un produit Cartésien de 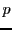 ensembles
sera formé de
ensembles
sera formé de 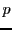 -uplets.
-uplets.
Une application d'un ensemble  vers un ensemble
vers un ensemble  est un objet
mathématique qui associe à tout élément
est un objet
mathématique qui associe à tout élément 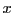 de
de  un unique
élément
un unique
élément 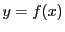 de
de  .
.  est l'ensemble de départ, et
est l'ensemble de départ, et
 est l'ensemble d'arrivée.
est l'ensemble d'arrivée.
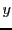 est l'image de
est l'image de 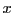 , et
, et 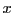 est l'antécédent de
est l'antécédent de 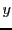 .
.
On utilisera dans la suite de ce cours les notions fondamentales suivantes:
- L'application
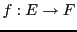 est injective si tout
est injective si tout 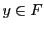 a au plus un
antécédent
a au plus un
antécédent 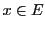 .
.
- L'application
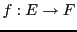 est surjective si tout
est surjective si tout 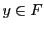 a au moins un
antécédent
a au moins un
antécédent 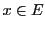 .
.
- L'application
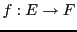 est bijective si elle est injective et
surjective, en d'autres termes si tout
est bijective si elle est injective et
surjective, en d'autres termes si tout 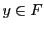 a un et un seul
antécédent
a un et un seul
antécédent 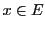 .
.
REMARQUE 1.3
Rappelons ce qu'est une fonction. Etant donnés deux ensembles

et

, une fonction
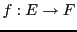
associe à tout élément de

1 ou 0 élément de

: ainsi, tout élément de

n'a pas nécessairement une image par la fonction
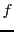
.
L'ensemble des éléments de  qui possèdent une image par la fonction
est appelé ensemble de définition de la fonction
qui possèdent une image par la fonction
est appelé ensemble de définition de la fonction 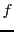 , noté
, noté 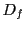 .
.
Ainsi, toute fonction 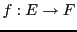 n'est pas nécessairement une application.
Par contre, la même fonction
n'est pas nécessairement une application.
Par contre, la même fonction 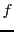 devient une application, si on change
l'ensemble de départ:
devient une application, si on change
l'ensemble de départ:
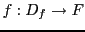 est une application.
est une application.
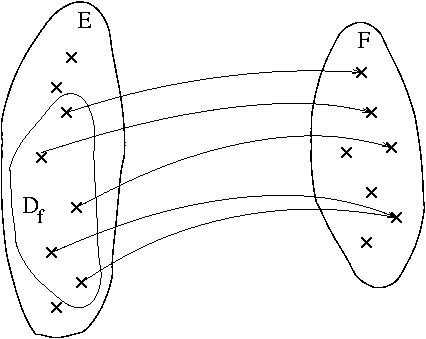
Un exemple de fonction se trouve en FIG. ![[*]](crossref.png) ,
représentée par un diagramme sagittal.
,
représentée par un diagramme sagittal.
Figure:
Diagramme sagittal d'une fonction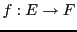 , qui devient
application par restriction à son domaine de définition
, qui devient
application par restriction à son domaine de définition  .
.
|
|
Un espace vectoriel est un ensemble dont les
éléments, appelés vecteurs, constituent une
généralisation abstraite de la notion usuelle (c'est à dire plus
géométrique) de vecteur. A ce titre, les éléments d'un espace
vectoriel peuvent être additionnés, et multipliés par des nombres.
Commençons par quelques exemples simples d'espaces
vectoriels ``classiques''.
EXEMPLE 1.3
Autre exemple: le
plan vectoriel, défini comme
l'ensemble des couples de réels
Les deux opérations précédentes sont encore bien définies:
- Addition:
pour tous
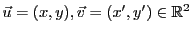 , on sait définir
, on sait définir
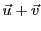 , qui appartient lui aussi à
, qui appartient lui aussi à
 , par la relation
, par la relation
- Multiplication par un scalaire
(ici un nombre réel):
pour tout
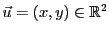 et pour tout
et pour tout
 ,
,
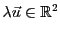 est de la forme
est de la forme
Dans ces deux cas ci-dessus, l'addition est commutative
(
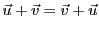 ) et associative
(
) et associative
(
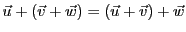 ); il existe un
vecteur nul
); il existe un
vecteur nul
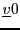 , tel que pour tout
, tel que pour tout
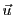 ,
,
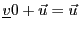 , et tout
vecteur
, et tout
vecteur 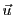 possède un opposé
(ou inverse), que l'on note
possède un opposé
(ou inverse), que l'on note
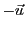 (voir en FIG.
(voir en FIG. ![[*]](crossref.png) ).
).
Figure:
Commutativité (à gauche) et associativité (à droite)
de l'addition
|
|
Quant à la multiplication par un scalaire, elle possède des
propriétés voisines (mais pas identiques): elle est commutative
(
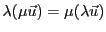 ) et distributive par rapport
à l'addition (
) et distributive par rapport
à l'addition (
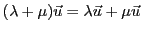 , et
, et
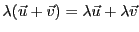 ). De plus, la
multiplication par le scalaire 1 ne change rien (
). De plus, la
multiplication par le scalaire 1 ne change rien (
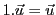 ).
).
Ces propriétés (avec d'autres) sont en fait des propriétés
``génériques'', qui permettent de définir la notion d'espace
vectoriel, comme on le verra.
On définit l'espace
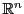 de la façon suivante.
de la façon suivante.

Dans
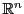 , ces deux opérations possèdent les mêmes propriétés
que celles que nous avons vues plus haut dans le cas de
, ces deux opérations possèdent les mêmes propriétés
que celles que nous avons vues plus haut dans le cas de
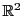 .
Elles font de
.
Elles font de
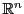 un
un
 -espace vectoriel, dont on donnera
la définition précise plus loin.
-espace vectoriel, dont on donnera
la définition précise plus loin.
En plus de sa structure d'espace vectoriel,
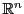 est également
équipé d'autres outils, comme la norme
(qui associe à tout vecteur sa ``longueur''), et
le produit scalaire
(qui associe à toute paire de vecteurs
un scalaire, décrivant leur ``ressemblance''), qui lui
confèrent une structure d'espace Euclidien.
est également
équipé d'autres outils, comme la norme
(qui associe à tout vecteur sa ``longueur''), et
le produit scalaire
(qui associe à toute paire de vecteurs
un scalaire, décrivant leur ``ressemblance''), qui lui
confèrent une structure d'espace Euclidien.
La norme d'un vecteur
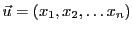 de
de
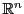 (qui représente donc sa ``longueur'') est définie par
(qui représente donc sa ``longueur'') est définie par
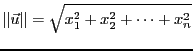 |
(1.1) |
Dans le cas de
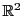 , cette égalité correspond au théorème de
Pythagore, si l'on identifie les deux composantes
, cette égalité correspond au théorème de
Pythagore, si l'on identifie les deux composantes 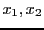 du couple
du couple
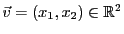 aux coordonnées Cartésiennes du point
aux coordonnées Cartésiennes du point 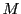 du
plan tel que
du
plan tel que
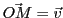 .
.
La norme vérifie l'inégalité triangulaire: pour tous
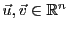 ,
,
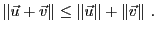 |
(1.2) |
Le produit scalaire de deux vecteurs est défini par
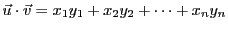 |
(1.3) |
et vérifie la propriété suivante, qui est essentielle
![\begin{proposition}[In\'egalit\'e de Cauchy-Schwarz]
\begin{equation}
\vert{\v...
... \le \Vert{\vec{u}}\Vert\,\Vert{\vec{v}}\Vert
\end{equation}
\end{proposition}](img120.png)
Interprétation: on a donc
et donc il existe
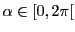 tel que
tel que
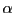 est l'angle entre les deux vecteurs
est l'angle entre les deux vecteurs 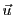 et
et 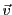 .
.
Ces opérations munissent
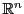 d'une structure
d'espace Euclidien.
Dans un premier temps, nous nous focaliserons
essentiellement sur la structure d'espace vectoriel, laissant de côté
les notions de norme et produit scalaire. Nous reviendrons sur ces notions
plus tard, lorsque nous traiterons la diagonalisation des matrices.
d'une structure
d'espace Euclidien.
Dans un premier temps, nous nous focaliserons
essentiellement sur la structure d'espace vectoriel, laissant de côté
les notions de norme et produit scalaire. Nous reviendrons sur ces notions
plus tard, lorsque nous traiterons la diagonalisation des matrices.
Définitions: espace vectoriel
La notion centrale de ce chapitre est la notion d'espace vectoriel.
On se limitera ici aux notions d'espaces vectoriels sur
 et
sur
et
sur
 , qui sont les plus couramment utilisées. On parlera de
, qui sont les plus couramment utilisées. On parlera de
 -espace vectoriel ou de
-espace vectoriel ou de
 -espace vectoriel. Lorsque les
propriétés étudiées sont vraies indifféremment dans les cas
réel ou complexe, on parlera de
-espace vectoriel. Lorsque les
propriétés étudiées sont vraies indifféremment dans les cas
réel ou complexe, on parlera de
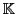 -espace vectoriel (
-espace vectoriel (
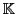 représentant génériquement
représentant génériquement
 ou
ou
 ), ou d'espace vectoriel
tout simplement.
), ou d'espace vectoriel
tout simplement.
![\begin{definition}[${\mathbb{R}}$-Espace vectoriel]
Un ${\mathbb{R}}$-espace ...
...quad&\forall{\vec{u}}\in E\ .
\end{eqnarray}
\end{enumerate}
\end{definition}](img127.png)
En sciences appliquées, en particulier en physique et en chimie,
on est souvent amené à manipuler des nombres complexes. C'est
pourquoi il est utile d'étendre la notion d'espace vectoriel
aux nombres complexes. La définition d'un
 -espace vectoriel
est presque identique à la définition d'un
-espace vectoriel
est presque identique à la définition d'un
 -espace vectoriel,
la seule différence étant que la multiplication par un scalaire
est cette fois la multiplication par un nombre complexe.
-espace vectoriel,
la seule différence étant que la multiplication par un scalaire
est cette fois la multiplication par un nombre complexe.
![\begin{definition}[$\mathbb{C}$-Espace vectoriel]
Un $\mathbb{C}$-espace vect...
...quad&\forall{\vec{u}}\in E\ .
\end{eqnarray}
\end{enumerate}
\end{definition}](img128.png)
REMARQUE 1.4
On peut vérifier que tout

-espace vectoriel est automatiquement
un

-espace vectoriel. La réciproque est fausse.
Outre les exemples géométriques (
 ) que nous avons vus plus haut,
on utilise souvent d'autres exemples d'espaces vectoriels, dans bien des
domaines.
) que nous avons vus plus haut,
on utilise souvent d'autres exemples d'espaces vectoriels, dans bien des
domaines.
- Le premier exemple qui vienne à l'esprit est celui de l'espace
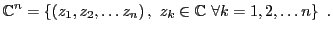 |
(1.4) |
on peut facilement vérifier que
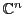 est un
est un
 -espace vectoriel,
dès lors que l'on définit l'addition et la multiplication par un
scalaire comme suit: pour tous
-espace vectoriel,
dès lors que l'on définit l'addition et la multiplication par un
scalaire comme suit: pour tous
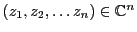 ,
,
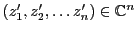 et
et
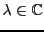 ,
,
et
-
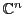 , et en particulier
, et en particulier
 , est également un
, est également un
 -espace vectoriel,
comme on peut le vérifier facilement.
-espace vectoriel,
comme on peut le vérifier facilement.
- Considérons l'ensemble des solutions d'un système homogène
de deux équations linéaires
où
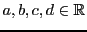 . L'ensemble des solutions est un sous-ensemble
de
. L'ensemble des solutions est un sous-ensemble
de
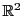 , dont on peut montrer qu'il s'agit d'un espace vectoriel,
lorsque l'on le munit de l'addition et la multiplication scalaire
de
, dont on peut montrer qu'il s'agit d'un espace vectoriel,
lorsque l'on le munit de l'addition et la multiplication scalaire
de
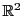 .
.
- Un autre exemple simple est l'exemple des espaces de polynômes.
Etant donné un entier
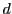 , on considère l'ensemble
, on considère l'ensemble
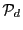 des polynômes de degré inférieur ou égal à
des polynômes de degré inférieur ou égal à 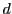 à coefficients
complexes, c'est à dire des fonctions
à coefficients
complexes, c'est à dire des fonctions
les nombres 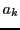 étant des nombres complexes. Cet ensemble de
polynômes est muni d'une structure de
étant des nombres complexes. Cet ensemble de
polynômes est muni d'une structure de
 -espace vectoriel, grâce
à l'addition et la multiplication par un scalaire suivantes:
pour tous polynômes
-espace vectoriel, grâce
à l'addition et la multiplication par un scalaire suivantes:
pour tous polynômes 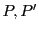 de degré inférieur ou égal à
de degré inférieur ou égal à 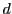 ,
et tout complexe
,
et tout complexe
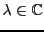 ,
, 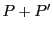 et
et 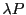 sont les polynômes définis par
sont les polynômes définis par
-
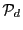 est également un
est également un
 -espace vectoriel.
L'ensemble des polynômes de degré inférieur ou égal à
-espace vectoriel.
L'ensemble des polynômes de degré inférieur ou égal à
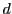 à coefficients réels est un
à coefficients réels est un
 -espace
vectoriel, mais pas un
-espace
vectoriel, mais pas un
 -espace vectoriel.
-espace vectoriel.
- On note
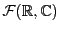 l'ensemble des fonctions définies sur
l'ensemble des fonctions définies sur
 , à valeurs dans
, à valeurs dans
 . On montre facilement qu'en
définissant l'addition des fonctions et leur multiplication par
un scalaire comme
. On montre facilement qu'en
définissant l'addition des fonctions et leur multiplication par
un scalaire comme
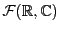 acquiert une structure de
acquiert une structure de
 -espace vectoriel.
-espace vectoriel.
- On considère l'ensemble des fonctions
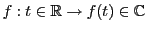 ,
solutions d'une équation différentielle linéaire homogène
donnée, par exemple
,
solutions d'une équation différentielle linéaire homogène
donnée, par exemple
On peut facilement vérifier que l'ensemble de ces solutions forme
un
 -espace vectoriel, en définissant l'addition et la multiplication
par un scalaire comme ci-dessus.
-espace vectoriel, en définissant l'addition et la multiplication
par un scalaire comme ci-dessus.

EXEMPLE 1.4
Par exemple, considérons l'espace vectoriel
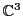
, et le sous-ensemble
Figure:
Le plan vectoriel dans
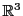 , d'équation
, d'équation 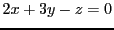 .
On note qu'il passe par l'origine.
.
On note qu'il passe par l'origine.
|
|
Il est possible de montrer que  est un sous-espace vectoriel de
est un sous-espace vectoriel de
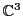 , c'est à dire que tous les axiomes des
définition
, c'est à dire que tous les axiomes des
définition ![[*]](crossref.png) et
et ![[*]](crossref.png) sont satisfaits.
On le démontrera un peu plus loin, de façon plus simple.
sont satisfaits.
On le démontrera un peu plus loin, de façon plus simple.
Etant donnés un espace vectoriel  et un sous-ensemble
et un sous-ensemble  ,
montrer que
,
montrer que  est un sous-espace vectoriel de
est un sous-espace vectoriel de  demande de
vérifier tous les axiomes de la définition
demande de
vérifier tous les axiomes de la définition ![[*]](crossref.png) . Cela
n'est en fait pas nécessaire, grâce au résultat suivant.
. Cela
n'est en fait pas nécessaire, grâce au résultat suivant.

Preuve:
Ces conditions sont évidemment nécessaires. Pour prouver qu'elles sont
suffisantes, remarquons que les axiomes (![[*]](crossref.png) )
à (
)
à (![[*]](crossref.png) ) sont satisfaits dans
) sont satisfaits dans  , et comme
, et comme
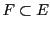 , ils sont donc sautomatiquement satisfaits dans
, ils sont donc sautomatiquement satisfaits dans  , à
l'exception de l'existence de l'élément neutre (
, à
l'exception de l'existence de l'élément neutre (![[*]](crossref.png) )
et de l'opposé (
)
et de l'opposé (![[*]](crossref.png) ), qu'il faut vérifier. Ces deux
propriétés sont conséquence des hypothèses: en effet, pour
tout
), qu'il faut vérifier. Ces deux
propriétés sont conséquence des hypothèses: en effet, pour
tout
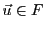 ,
,
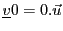 , de sorte que
, de sorte que
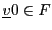 . De plus,
pour tout
. De plus,
pour tout
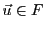 ,
,
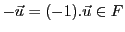 , ce qui conclut la
démonstration.
, ce qui conclut la
démonstration.
De façon plus générale, on déduit de ce résultat le
corollaire

Preuve: Il suffit de démontrer que (![[*]](crossref.png) )
est équivalente aux équations (
)
est équivalente aux équations (![[*]](crossref.png) ) et (
) et (![[*]](crossref.png) ),
ce qui est immédiat.
),
ce qui est immédiat.
Revenons à l'exemple ![[*]](crossref.png) ci-dessus. Pour montrer qu'un tel
ci-dessus. Pour montrer qu'un tel
 est un sous-espace vectoriel de
est un sous-espace vectoriel de
 , il suffit donc de montrer que
, il suffit donc de montrer que
 est non-vide, ce qui est assuré dès lors que l'on remarque que
par exemple,
est non-vide, ce qui est assuré dès lors que l'on remarque que
par exemple,
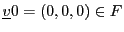 , et que pour tous
, et que pour tous
 et
et
 , (
, (![[*]](crossref.png) ) est satisfaite.
Considérons donc
) est satisfaite.
Considérons donc
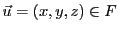 et
et
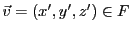 , et
calculons, pour des
, et
calculons, pour des
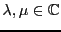 quelconques,
quelconques,
Alors, on voit facilement que
car
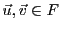 . Ceci prouve donc que ce
. Ceci prouve donc que ce  est bien un
sous-espace vectoriel de
est bien un
sous-espace vectoriel de
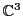 . Il s'agit d'un plan vectoriel.
. Il s'agit d'un plan vectoriel.
Soit  un espace vectoriel (réel ou complexe) et soient
un espace vectoriel (réel ou complexe) et soient
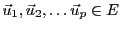
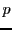 vecteurs de
vecteurs de  .
Si
.
Si
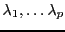 sont
sont 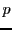 scalaires,
alors on dit que le vecteur
scalaires,
alors on dit que le vecteur
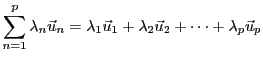 |
(1.5) |
est une combinaison linéaire
des vecteurs
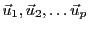 .
.

On dit aussi que la famille
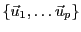 engendre
engendre  ,
et on note
,
et on note
Notons qu'il existe toujours une infinité de familles
génératrices pour un espace vectoriel.
EXEMPLE 1.6
Reprenons l'exemple du plan vectoriel

de l'exemple
![[*]](crossref.png)
.
Il est facile de voir que tout
est de la forme
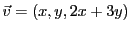
.
On peut alors écrire
de sorte que les vecteurs
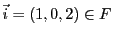
et
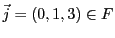
forment une
famille génératrice de

.
Considérons maintenant les vecteurs
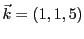 et
et 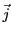 . Ces deux
vecteurs forment ils une famille génératrice de
. Ces deux
vecteurs forment ils une famille génératrice de  ?
?
Pour s'en assurer, soit
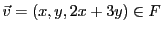 , quelconque. La question est,
``existe-t-il
, quelconque. La question est,
``existe-t-il
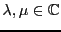 tels que
tels que
Cette équation vectorielle est équivalente au système de
trois équations linéaires à deux inconnues (
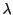
et
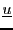
)
Par substitution, ce système est équivalent à
qui est lui même équivalent à
Ainsi, pour tous
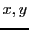
, on a bien trouvé
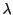
et
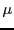
satisfaisant
à la condition ci-dessus, donc la famille
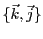
est bien
une famille génératrice pour

.
On vérifie aussi facilement que pour tout
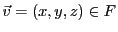 , on peut écrire par exemple
, on peut écrire par exemple
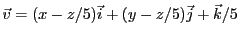 , de sorte que la
famille
, de sorte que la
famille
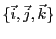 engendre
engendre  elle aussi.
elle aussi.

Par exemple,
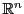 et
et
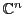 sont de dimension finie. Par contre,
on peut trouver beaucoup d'exemples d'espaces vectoriels de dimension
infinie, comme des espaces vectoriels de suites ou de fonctions.
On ne considèrera pas de tels exemples dans ce cours.
sont de dimension finie. Par contre,
on peut trouver beaucoup d'exemples d'espaces vectoriels de dimension
infinie, comme des espaces vectoriels de suites ou de fonctions.
On ne considèrera pas de tels exemples dans ce cours.

Preuve: Soit
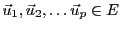 une famille
libre de
une famille
libre de 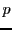 vecteurs dans
vecteurs dans  , et supposons qu'il existe
des nombres
, et supposons qu'il existe
des nombres
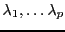 et
et
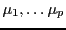 tels que
tels que
Alors on en déduit que
d'où, la famille
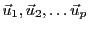 étant libre,
étant libre,
et donc
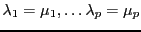 .
.
EXEMPLE 1.8
Dans
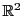
, considérons deux vecteurs orthogonaux
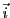
et
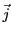
, comme
dans la F
IG. ![[*]](crossref.png)
, et posons
Figure:
Un seul développementUne infinité de développements
|
|
La famille
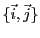 est une famille libre, alors que la famille
est une famille libre, alors que la famille
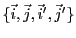 est une famille liée. Ceci se traduit par le
fait qu'un vecteur quelconque de
est une famille liée. Ceci se traduit par le
fait qu'un vecteur quelconque de
 s'écrit de façon unique comme
combinaison linéaire de
s'écrit de façon unique comme
combinaison linéaire de 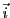 et
et 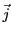 , alors qu'il existe une infinité de
façons différentes de l'écrire comme combinaison linéaire
de
, alors qu'il existe une infinité de
façons différentes de l'écrire comme combinaison linéaire
de 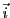 ,
, 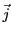 ,
,
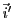 et
et
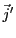 . En effet, considérons par exemple le
vecteur
. En effet, considérons par exemple le
vecteur
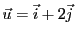 . Cette expression constitue l'unique
écriture de
. Cette expression constitue l'unique
écriture de 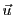 comme combinaison linéaire de
comme combinaison linéaire de 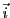 et
et 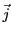 .
Par contre, on peut également écrire, pour tout
.
Par contre, on peut également écrire, pour tout
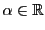 ,
,
Ceci étant vrai pour tout
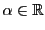
, on obtient ainsi une infinité
de décompositions possibles.
REMARQUE 1.5
Dans un
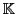
-espace vectoriel, la notion de dépendance linéaire ou
indépendance linéaire d'une famille de vecteurs dépend évidemment de
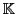
. Par exemple, prenons
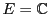
qui, comme nous l'avons vu, peut être
muni d'une structure de
-espace vectoriel et de

-espace vectoriel.
Dans le

-espace vectoriel

, la famille de vecteurs
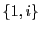
est une famille libre: en effet, il n'existe pas
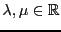
, non
simultanément nuls, tels que
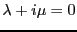
. Par contre, dans le

-espace vectoriel

, il s'agit d'une famille liée, car on peut
trouver
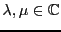
, non simultanément nuls, tels
que
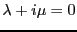
(prendre
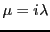
). Pour préciser les
choses, on parle parfois de famille
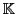
-libre ou
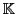
-liée
(
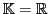
ou

).
Clairement, toute famille libre n'est pas obligatoirement
génératrice, et toute famille génératrice n'est pas
obligatoirement libre. La notion de base représente en quelque sorte
le ``juste compromis'' entre ces deux notions, comme on va le voir dans
l'exemple qui suit.
EXEMPLE 1.9
Reprenons l'exemple du

-espace vectoriel
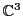
.
Les vecteurs
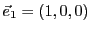
,
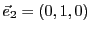
et
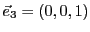
forment une famille dont on vérifie facilement qu'elle est
- Libre: soit
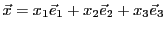 une combinaison
linéaire quelconque de
une combinaison
linéaire quelconque de
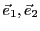 et
et
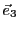 . Alors
. Alors
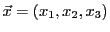 , et
, et
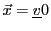 implique
implique
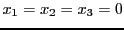 .
.
- Génératrice: pour tout
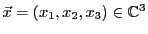 , on a
obligatoirement
, on a
obligatoirement
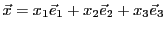 .
.
Il est clair que si l'on enlève un élément à cette famille,
la famille résultante n'est plus génératrice: par exemple, tout
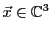
ne peut pas s'écrire comme combinaison linéaire de
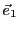
et
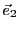
seuls. Par contre, si on ajoute n'importe quel vecteur
à cette famille, la famille résultante ne sera pas libre, le nouveau
vecteur pouvant s'exprimer comme combinaison linéaire des trois premiers.
Ainsi, la famille
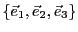 représente le
bon compromis pour écrire les éléments de
représente le
bon compromis pour écrire les éléments de
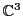 comme
combinaisons linéaires. C'est ce que l'on appelle une base de
comme
combinaisons linéaires. C'est ce que l'on appelle une base de
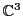 ,
en l'occurrence la base canonique de
,
en l'occurrence la base canonique de
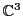 .
.

Dans le cas de
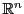 , la base canonique
de
, la base canonique
de
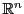 est la famille constituée des vecteurs
est la famille constituée des vecteurs
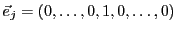 , pour
, pour
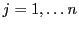 , le seul
élément non-nul du vecteur étant le
, le seul
élément non-nul du vecteur étant le 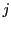 -ième.
-ième.
Le théorème qui suit, que nous donnons sans démonstration, est
un résultat fondamental.
![\begin{theorem}[Th\'eor\\lq eme de la dimension]
Soit $E$\ un $\mathbb{K}$-espac...
...playmath}
\dim_\mathbb{K}(E)
\end{displaymath}
\end{enumerate}
\end{theorem}](img260.png)
Par exemple, la dimension de
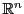 est égale à
est égale à  , la base canonique
de
, la base canonique
de
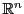 ayant
ayant  éléments.
éléments.
Pour illustrer ce résultat, il est utile de considérer un exemple simple.
EXEMPLE 1.10
Dans
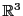
, on considère les deux vecteurs
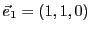
et
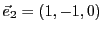
. On voit facilement qu'ils forment
une famille libre, et qu'on peut toujours leur adjoindre une troisième
vecteur, par exemple
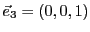
pour obtenir une famille génératrice.
Similairement, partant d'une famille génératrice de 4 vecteurs de
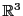 ,
on voit facilement qu'on peut lui enlever un vecteur, la famille résultante
étant maintenant libre, et toujours génératrice.
,
on voit facilement qu'on peut lui enlever un vecteur, la famille résultante
étant maintenant libre, et toujours génératrice.
REMARQUE 1.6
Notons que la dépendance de la dimension
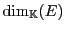
d'un
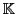
-espace vectoriel est un aspect important. Prenons par exemple
le cas de

. La dimension de

change selon que

est considéré comme

-espace vectoriel ou

-espace vectoriel. On peut facilement montrer que
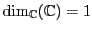
, alors que
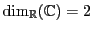
.
Ce résultat a de nombreuses conséquences ``pratiques''. Celle qui
suit se démontre aisément.

Preuve: Considérons une famille de plus de  vecteurs,
et supposons qu'elle soit libre; d'après le théorème de la dimension,
elle peut être complétée pour former une base, mais celle-ci aurait
alors plus de
vecteurs,
et supposons qu'elle soit libre; d'après le théorème de la dimension,
elle peut être complétée pour former une base, mais celle-ci aurait
alors plus de  vecteurs, ce qui est impossible. Donc la famille ne peut
être libre. Considérons maintenant une famille de moins de
vecteurs, ce qui est impossible. Donc la famille ne peut
être libre. Considérons maintenant une famille de moins de  vecteurs,
et supposons qu'elle soit génératrice. On peut alors en extraire une
base, qui aurait alors moins de
vecteurs,
et supposons qu'elle soit génératrice. On peut alors en extraire une
base, qui aurait alors moins de  vecteurs, ce qui est encore une fois
impossible. La famille ne peut donc pas êtretre génératrice.
vecteurs, ce qui est encore une fois
impossible. La famille ne peut donc pas êtretre génératrice.
Soit  un espace vectoriel de dimension
un espace vectoriel de dimension  , et soit
, et soit
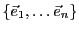 une famille libre de
une famille libre de  vecteurs de
vecteurs de  .
Supposons qu'elle ne soit pas génératrice. Alors d'après
le 2) du théorème
.
Supposons qu'elle ne soit pas génératrice. Alors d'après
le 2) du théorème ![[*]](crossref.png) , on peut la compléter pour
former une base de
, on peut la compléter pour
former une base de  . Mais celle-ci a alors plus de
. Mais celle-ci a alors plus de
 éléments, ce qui est impossible. Donc la
famille
éléments, ce qui est impossible. Donc la
famille
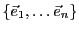 est nécessairement génératrice.
est nécessairement génératrice.
Similairement, soit
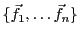 une famille génératrice
de
une famille génératrice
de  , supposons qu'elle ne soit pas libre. Alors d'après
le 1) du théorème
, supposons qu'elle ne soit pas libre. Alors d'après
le 1) du théorème ![[*]](crossref.png) , on peut lui enlever des
éléments pour obtenir une base, mais celle-ci compte moins de
, on peut lui enlever des
éléments pour obtenir une base, mais celle-ci compte moins de  éléments, ce qui est impossible. Donc la famille
éléments, ce qui est impossible. Donc la famille
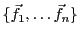 est obligatoirement libre.
est obligatoirement libre.
On a donc montré

Finalement, on déduit de la définition d'une
famille génératrice et de la proposition ![[*]](crossref.png) l'existence et l'unicité du développement d'un vecteur sur une base:
l'existence et l'unicité du développement d'un vecteur sur une base:
![\begin{theorem}[Unicit\'e du d\'eveloppement sur une base]
Soit $E$\ un espace ...
...c}
x_1\\ x_2\\ \vdots\\ x_n\end{array}\right)
\end{displaymath}
\end{theorem}](img272.png)
Dans le cas simple de
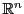 (ou
(ou
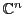 ), dont on a vu plus haut
la base canonique, il est facile de voir
que les composantes d'un vecteur
), dont on a vu plus haut
la base canonique, il est facile de voir
que les composantes d'un vecteur
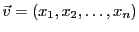 dans
cette base canonique ne sont autres que les nombres
dans
cette base canonique ne sont autres que les nombres
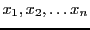 .
.
Dans un cas plus général, la détermination des composantes
d'un vecteur sur une base demande un peu plus de travail.
EXEMPLE 1.11
Comment déterminer les composantes d'un vecteur par rapport
à une base ?
Prenons l'exemple de
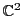
, et de la base constituée par les deux vecteurs
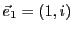
et
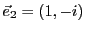
. Considérons un vecteur de
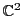
, par
exemple
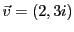
. On cherche à écrire
ce qui revient à résoudre le système
Ce système se résoud facilement, et conduit à
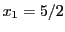
et
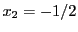
.
Dans des cas plus complexes, il est possible d'utiliser des techniques
plus systématiques, comme par exemple la méthode du pivot de Gauss,
décrite un peu pus loin.
Soient  et
et 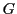 deux sous-espaces vectoriels d'un espace vectoriel
deux sous-espaces vectoriels d'un espace vectoriel  .
On considère la réunion de
.
On considère la réunion de  et
et 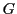
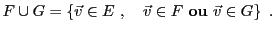 |
(1.6) |
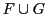 est clairement un sous-ensemble de
est clairement un sous-ensemble de  , par construction.
Par contre, ça n'est pas un sous-espace vectoriel de
, par construction.
Par contre, ça n'est pas un sous-espace vectoriel de  en
général.
en
général.
EXEMPLE 1.12
Prenons
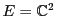
, et

et
sont deux sous-espaces vectoriels de

(de dimension
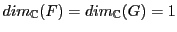
). Par contre,
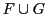
n'est pas un
sous-espace vectoriel de

, donc n'est pas un espace vectoriel.
Par exemple, soient
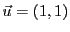
et
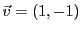
, ils appartiennent
tous deux à
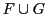
, mais
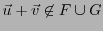
.
Considérons maintenant l'intersection 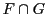 de deux sous-espaces
vectoriels
de deux sous-espaces
vectoriels  et
et 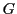 de
de 
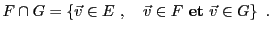 |
(1.7) |
Soient
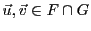 . Alors
. Alors
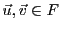 et
et
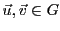 ;
donc,
;
donc,  et
et 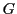 étant des sous-espaces vectoriels de
étant des sous-espaces vectoriels de  ,
,
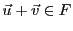 et
et
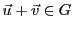 , d'où
, d'où
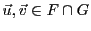 .
On a ainsi montré
.
On a ainsi montré

EXEMPLE 1.13
Si nous reprenons l'exemple précédent, nous voyons bien que
est limité au seul vecteur nul de
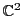
... ce qui est bien un sous-espace
vectoriel, de dimension 0.
Etant donnés deux sous-espaces vectoriels  et
et 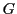 d'un
espace vectoriel donné
d'un
espace vectoriel donné  , il est possible de considérer l'ensemble
formé des sommes d'éléments de
, il est possible de considérer l'ensemble
formé des sommes d'éléments de  et
et 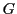 . Il est facile de montrer
que cet ensemble est en fait un espace vectoriel.
. Il est facile de montrer
que cet ensemble est en fait un espace vectoriel.

Supposons que 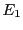 et
et 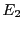 soient deux sous-espaces vectoriels de
soient deux sous-espaces vectoriels de  ,
et soit
,
et soit
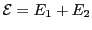 . Soit
. Soit
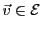 . Alors il existe
. Alors il existe
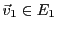 et
et
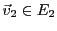 tels que
tels que
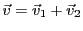 . Supposons qu'il existe
un autre couple de vecteurs
. Supposons qu'il existe
un autre couple de vecteurs
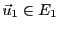 et
et
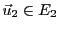 tels que
tels que
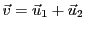 . Alors on a
. Alors on a
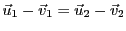 ,
c'est à dire une égalité entre un vecteur de
,
c'est à dire une égalité entre un vecteur de 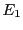 et un vecteur
de
et un vecteur
de 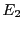 . A ce point, de deux choses l'une: soit
. A ce point, de deux choses l'une: soit
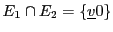 ,
auquel cas ces deux vecteurs sont nécessairement nuls. Soit
,
auquel cas ces deux vecteurs sont nécessairement nuls. Soit
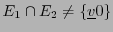 , et on peut avoir
, et on peut avoir
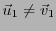 et
et
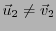 . On a donc montré
. On a donc montré

Qu'en est-il de la dimension de la somme de deux sous-espaces vectoriels
de dimension finie ? Si  et
et  sont de dimension finie, disons
sont de dimension finie, disons  et
et  , alors ils admettent chacun une base de respectivement
, alors ils admettent chacun une base de respectivement 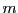 et
et
 élements. L'union de ces deux bases est une famille génératrice
de
élements. L'union de ces deux bases est une famille génératrice
de 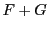 , qui est ainsi de dimension inférieure ou égale à
, qui est ainsi de dimension inférieure ou égale à
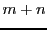 . Si la somme
. Si la somme 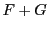 est une somme directe, c'est à dire si
est une somme directe, c'est à dire si
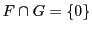 , alors l'union des deux bases est cette fois une base
de
, alors l'union des deux bases est cette fois une base
de 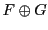 , et la dimension de
, et la dimension de 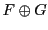 est alors égale à
est alors égale à 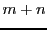 .
On a donc montré
.
On a donc montré
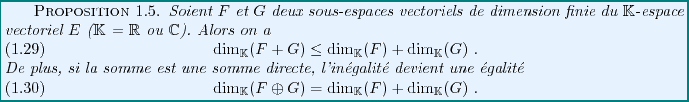
EXEMPLE 1.14
Prenons
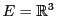
, et soient
On voit facilement que
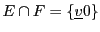
, donc la somme
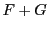
est une somme directe. De plus,

est de dimension 2
(par exemple, une base de

est donnée par les vecteurs
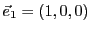
et
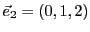
), et
est de dimension
(base:
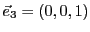
).

On a alors
Dans l'exemple ![[*]](crossref.png) ci-dessus, cette égalité
est bien vérifiée.
ci-dessus, cette égalité
est bien vérifiée.

EXEMPLE 1.15
Prenons
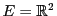
, et soit
une droite vectorielle.
Alors, on peut vérifier que les supplémentaires de

sont toutes les droites vectorielles du plan
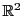
différentes
de

.
La méthode du pivot de Gauss
(ou élimination de Gauss)
est une technique simple et puissante de résolution de
systèmes linéaires, de la forme
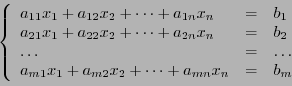 |
(1.8) |
les 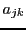 et les
et les 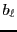 étant
étant 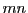 et
et 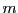 scalaires,
respectivement, et
scalaires,
respectivement, et
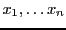 étant les
étant les  inconnues.
inconnues.
Commençons par l'illustrer sur un exemple, avant de
voir en quoi elle peut être utile pour résoudre des problèmes simples
d'algèbre linéaire.
La base de la méthode du pivot de Gauss pour la résolution
de systèmes linéaires est l'ensemble des trois propriétés
fondamentales: La solution d'un système d'équations linéaires
ne change pas si
- On permute l'ordre des équations
- On multiplie (terme à terme) une équation par un scalaire non-nul.
- On ajoute à une équation une combinaison linéaire quelconque
des autres équations
Considérons le système linéaire de trois équations à trois inconnues
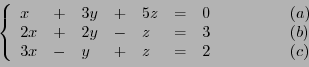 |
(1.9) |
La méthode de Gauss consiste à substituer à ce système un
autre système d'équations, équivalent, dans lequel on élimine
par substitutions successives des variables. Par exemple,
dans le cas qui nous intéresse, en remplaçant les deux dernières
équations 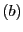 et
et 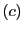 par
par 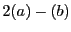 et
et 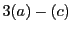 respectivement
(au sens de la soustraction des équations ``terme à terme''),
on obtient
respectivement
(au sens de la soustraction des équations ``terme à terme''),
on obtient
puis en substituant à 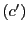 l'équation
l'équation
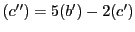 , on obtient le
système étagé suivant
, on obtient le
système étagé suivant
qui est facile à résoudre: 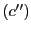 donne
donne 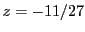 , puis en
substituant dans
, puis en
substituant dans 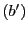 on obtient
on obtient
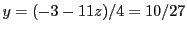 , puis finalement
, puis finalement
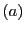 donne
donne
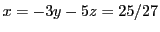 .
.
La méthode du pivot de Gauss possède de nombreuses applications.
Par exemple, étant donnée une famille de vecteurs, elle peut permettre
de dire si cette famille est une famille libre.
En d'autres termes, étant donnés un certain nombre de vecteurs
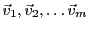 de
de
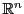 (ou
(ou
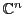 ) (avec
) (avec 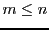 , sans quoi
la famille est automatiquement liée), existe-t-il des scalaires
, sans quoi
la famille est automatiquement liée), existe-t-il des scalaires
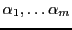 tels que
tels que
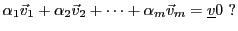 |
(1.10) |
S'il existe de tels scalaires, non simultanément nuls, alors
la famille est liée. Sinon, la famille est libre.
Si l'on connait les composantes des vecteurs
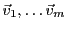 dans la base canonique, cette équation vectorielle peut s'écrire comme
un système de
dans la base canonique, cette équation vectorielle peut s'écrire comme
un système de  équations linéaires, que l'on
peut résoudre par la méthode du pivot.
équations linéaires, que l'on
peut résoudre par la méthode du pivot.
EXEMPLE 1.16
Dans
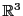
, considérons les vecteurs
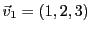
,
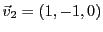
et
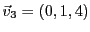
, et cherchons une éventuelle
relation de la forme
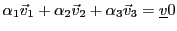
.
Cette équation vectorielle se ramène alors au système
Le pivot de Gauss permet de transformer ce système en
puis
qui implique
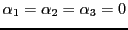
. Le système
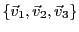
est bien un système libre dans
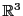
(et en est donc une base).
Une autre question reliée, qui peut également être
traitée par élimination de Gauss: étant donnée une famille
de vecteurs, trouver (s'il en existe) une relation linéaire
entre ces vecteurs.
Cette question se formule de façon identique à la précédente:
il faut trouver les scalaires
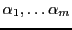 dans (
dans (![[*]](crossref.png) ).
).
EXEMPLE 1.17
Dans
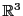
, considérons les vecteurs
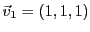
,
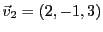
et
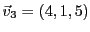
, et cherchons une éventuelle
relation de la forme
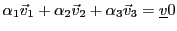
.
Cette équation vectorielle se ramène alors au système
Le pivot de Gauss permet de transformer ce système en
et il n'est pas nécessaire d'aller plus loin pour voir que les
deux dernières équations sont équivalentes, et donnent
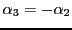
, d'où
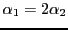
.
La relation linéaire recherchée est donc, en
prenant
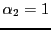
,
ce que l'on peut encore écrire
de sorte que tout
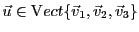
s'écrit comme combinaison linéaire de
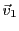
et
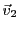
.
Ainsi
qui est un sous-espace vectoriel de
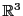
de dimension deux (car la famille
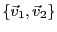
est une famille libre.
On verra plus bas comment caractériser ce sous-espace vectoriel.
En d'autres termes, étant donnés un certain nombre de vecteurs
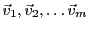 de
de
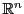 (ou
(ou
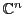 ) (avec
) (avec 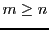 , sans quoi
la famille ne peut être génératrice), peut-on trouver pour tout
, sans quoi
la famille ne peut être génératrice), peut-on trouver pour tout
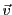 des scalaires
des scalaires
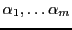 tels que
tels que
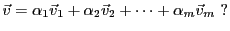
Si l'on connait les composantes des vecteurs
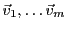 ,
dans la base canonique, cette équation vectorielle peut s'écrire comme
un système de
,
dans la base canonique, cette équation vectorielle peut s'écrire comme
un système de  équations linéaires (inhomogène cette fois),
que l'on peut résoudre par la méthode du pivot.
équations linéaires (inhomogène cette fois),
que l'on peut résoudre par la méthode du pivot.
EXEMPLE 1.18
Dans
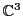
, considérons les vecteurs
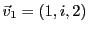
,
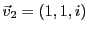
et
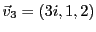
. Soit
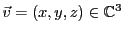
, quelconque, la question
est de savoir si l'on peut écrire
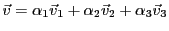
. Cette équation
vectorielle est équivalente à un système inhomogène
de trois équations linéaires
Le pivot de Gauss permet de transformer ce système en
puis en
La troisième équation se simplifie en
d'où on déduit ensuite
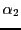
puis
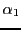
par
Ainsi, pour tout
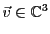
, on a bien pu l'exprimer comme combinaison
linéaire de
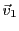
,
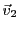
, et
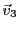
, ces trois vecteurs
constituent donc une famille génératrice de
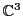
.
EXEMPLE ![[*]](crossref.png) (SUITE)
Comment caractériser le sous-espace vectoriel de
(SUITE)
Comment caractériser le sous-espace vectoriel de
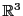 engendré
par les vecteurs
engendré
par les vecteurs
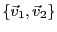 ? Il suffit de considérer
un vecteur quelconque
? Il suffit de considérer
un vecteur quelconque
En posant
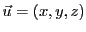 , on a donc
, on a donc
syst ème qui se met sous la forme
d'où on déduit que
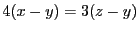 , et donc l'équation de
, et donc l'équation de
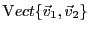
Notons qu'on aurait obtenu exactement le même résultat en exprimant 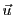 comme combinaison linéaire de
comme combinaison linéaire de
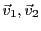 et
et
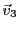 ... au prix de calculs
un peu plus longs.
... au prix de calculs
un peu plus longs.
Bruno Torresani
2009-02-18
![]() et
et ![]() sont deux solutions d'un problème donné, alors
sont deux solutions d'un problème donné, alors ![]() est
solution également, ainsi que
est
solution également, ainsi que ![]() pour tout nombre
(appelé scalaire)
pour tout nombre
(appelé scalaire) ![]() .
.
![]() ), notation qu'on oubliera ensuite.
), notation qu'on oubliera ensuite.
![]() est inclus dans un ensemble
est inclus dans un ensemble ![]() , relation que l'on note
, relation que l'on note
![]() , c'est à dire l'ensemble
constitué de l'unique élément
, c'est à dire l'ensemble
constitué de l'unique élément ![]() , est un sous-ensemble de
, est un sous-ensemble de
![]() .
On note cela
.
On note cela
![]() et
et ![]() , leur union
, leur union ![]() est l'ensemble
formé des éléments de
est l'ensemble
formé des éléments de ![]() et des éléments de
et des éléments de ![]()
![]() et
et ![]() , on a parfois à considérer
l'ensemble des éléments de
, on a parfois à considérer
l'ensemble des éléments de ![]() qui n'appartiennent pas à
qui n'appartiennent pas à ![]() .
Cet ensemble est appelé la différence ``
.
Cet ensemble est appelé la différence ``![]() moins
moins ![]() '', et est noté
'', et est noté
![]() et
et ![]() , notée
, notée
![]() , qui est constituée des éléments de
, qui est constituée des éléments de ![]() n'appartenant
pas à
n'appartenant
pas à ![]() et des éléments de
et des éléments de ![]() n'appartenant pas à
n'appartenant pas à ![]() :
:
![]() et
et ![]() , le produit cartésien de
, le produit cartésien de ![]() et
et ![]() ,
noté
,
noté ![]() , est l'ensemble des couples dont le premier élément
appartient à
, est l'ensemble des couples dont le premier élément
appartient à ![]() et le second appartient à
et le second appartient à ![]() :
:
![]() ensembles
sera formé de
ensembles
sera formé de ![]() -uplets.
-uplets.
![]() qui possèdent une image par la fonction
est appelé ensemble de définition de la fonction
qui possèdent une image par la fonction
est appelé ensemble de définition de la fonction ![]() , noté
, noté ![]() .
.
![]() n'est pas nécessairement une application.
Par contre, la même fonction
n'est pas nécessairement une application.
Par contre, la même fonction ![]() devient une application, si on change
l'ensemble de départ:
devient une application, si on change
l'ensemble de départ:
![]() est une application.
est une application.
![[*]](crossref.png) ,
représentée par un diagramme sagittal.
,
représentée par un diagramme sagittal.
![[*]](crossref.png) ).
).
![]() ) et distributive par rapport
à l'addition (
) et distributive par rapport
à l'addition (
![]() , et
, et
![]() ). De plus, la
multiplication par le scalaire 1 ne change rien (
). De plus, la
multiplication par le scalaire 1 ne change rien (
![]() ).
).
![]() de la façon suivante.
de la façon suivante.

![]() , ces deux opérations possèdent les mêmes propriétés
que celles que nous avons vues plus haut dans le cas de
, ces deux opérations possèdent les mêmes propriétés
que celles que nous avons vues plus haut dans le cas de
![]() .
Elles font de
.
Elles font de
![]() un
un
![]() -espace vectoriel, dont on donnera
la définition précise plus loin.
-espace vectoriel, dont on donnera
la définition précise plus loin.
![]() de
de
![]() (qui représente donc sa ``longueur'') est définie par
(qui représente donc sa ``longueur'') est définie par
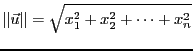
![]() ,
,
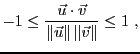
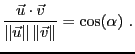
![]() d'une structure
d'espace Euclidien.
Dans un premier temps, nous nous focaliserons
essentiellement sur la structure d'espace vectoriel, laissant de côté
les notions de norme et produit scalaire. Nous reviendrons sur ces notions
plus tard, lorsque nous traiterons la diagonalisation des matrices.
d'une structure
d'espace Euclidien.
Dans un premier temps, nous nous focaliserons
essentiellement sur la structure d'espace vectoriel, laissant de côté
les notions de norme et produit scalaire. Nous reviendrons sur ces notions
plus tard, lorsque nous traiterons la diagonalisation des matrices.
![\begin{definition}[${\mathbb{R}}$-Espace vectoriel]
Un ${\mathbb{R}}$-espace ...
...quad&\forall{\vec{u}}\in E\ .
\end{eqnarray}
\end{enumerate}
\end{definition}](img127.png)
![]() -espace vectoriel
est presque identique à la définition d'un
-espace vectoriel
est presque identique à la définition d'un
![]() -espace vectoriel,
la seule différence étant que la multiplication par un scalaire
est cette fois la multiplication par un nombre complexe.
-espace vectoriel,
la seule différence étant que la multiplication par un scalaire
est cette fois la multiplication par un nombre complexe.
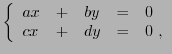
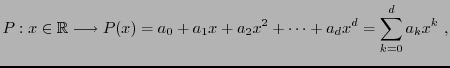

![]() est un sous-espace vectoriel de
est un sous-espace vectoriel de
![]() , c'est à dire que tous les axiomes des
définition
, c'est à dire que tous les axiomes des
définition ![[*]](crossref.png) et
et ![[*]](crossref.png) sont satisfaits.
On le démontrera un peu plus loin, de façon plus simple.
sont satisfaits.
On le démontrera un peu plus loin, de façon plus simple.
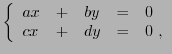
![]() et un sous-ensemble
et un sous-ensemble ![]() ,
montrer que
,
montrer que ![]() est un sous-espace vectoriel de
est un sous-espace vectoriel de ![]() demande de
vérifier tous les axiomes de la définition
demande de
vérifier tous les axiomes de la définition ![[*]](crossref.png) . Cela
n'est en fait pas nécessaire, grâce au résultat suivant.
. Cela
n'est en fait pas nécessaire, grâce au résultat suivant.

![[*]](crossref.png) )
à (
)
à (![[*]](crossref.png) ) sont satisfaits dans
) sont satisfaits dans ![]() , et comme
, et comme
![]() , ils sont donc sautomatiquement satisfaits dans
, ils sont donc sautomatiquement satisfaits dans ![]() , à
l'exception de l'existence de l'élément neutre (
, à
l'exception de l'existence de l'élément neutre (![[*]](crossref.png) )
et de l'opposé (
)
et de l'opposé (![[*]](crossref.png) ), qu'il faut vérifier. Ces deux
propriétés sont conséquence des hypothèses: en effet, pour
tout
), qu'il faut vérifier. Ces deux
propriétés sont conséquence des hypothèses: en effet, pour
tout
![]() ,
,
![]() , de sorte que
, de sorte que
![]() . De plus,
pour tout
. De plus,
pour tout
![]() ,
,
![]() , ce qui conclut la
démonstration.
, ce qui conclut la
démonstration.
![]()

![[*]](crossref.png) )
est équivalente aux équations (
)
est équivalente aux équations (![[*]](crossref.png) ) et (
) et (![[*]](crossref.png) ),
ce qui est immédiat.
),
ce qui est immédiat.
![]()
![[*]](crossref.png) ci-dessus. Pour montrer qu'un tel
ci-dessus. Pour montrer qu'un tel
![]() est un sous-espace vectoriel de
est un sous-espace vectoriel de
![]() , il suffit donc de montrer que
, il suffit donc de montrer que
![]() est non-vide, ce qui est assuré dès lors que l'on remarque que
par exemple,
est non-vide, ce qui est assuré dès lors que l'on remarque que
par exemple,
![]() , et que pour tous
, et que pour tous
![]() et
et
![]() , (
, (![[*]](crossref.png) ) est satisfaite.
Considérons donc
) est satisfaite.
Considérons donc
![]() et
et
![]() , et
calculons, pour des
, et
calculons, pour des
![]() quelconques,
quelconques,
![]() engendre
engendre ![]() ,
et on note
,
et on note
![[*]](crossref.png) .
Il est facile de voir que tout
.
Il est facile de voir que tout
![]() et
et ![]() . Ces deux
vecteurs forment ils une famille génératrice de
. Ces deux
vecteurs forment ils une famille génératrice de ![]() ?
?
![]() , quelconque. La question est,
``existe-t-il
, quelconque. La question est,
``existe-t-il
![]() tels que
tels que
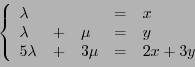
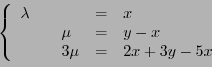
![]() , on peut écrire par exemple
, on peut écrire par exemple
![]() , de sorte que la
famille
, de sorte que la
famille
![]() engendre
engendre ![]() elle aussi.
elle aussi.
![]()
![]() et
et
![]() sont de dimension finie. Par contre,
on peut trouver beaucoup d'exemples d'espaces vectoriels de dimension
infinie, comme des espaces vectoriels de suites ou de fonctions.
On ne considèrera pas de tels exemples dans ce cours.
sont de dimension finie. Par contre,
on peut trouver beaucoup d'exemples d'espaces vectoriels de dimension
infinie, comme des espaces vectoriels de suites ou de fonctions.
On ne considèrera pas de tels exemples dans ce cours.
![[*]](crossref.png) ci-dessus.
On peut vérifier que
ci-dessus.
On peut vérifier que
![]() . Soit
. Soit
![]() ,
et supposons
,
et supposons
![]() . Ceci implique que
. Ceci implique que
![]() ,
équation qui admet des solutions non-nulles:
,
équation qui admet des solutions non-nulles:
![]() . Donc la famille
. Donc la famille
![]() est liée.
est liée.

![[*]](crossref.png) , et posons
, et posons
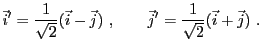
![]() est une famille libre, alors que la famille
est une famille libre, alors que la famille
![]() est une famille liée. Ceci se traduit par le
fait qu'un vecteur quelconque de
est une famille liée. Ceci se traduit par le
fait qu'un vecteur quelconque de
![]() s'écrit de façon unique comme
combinaison linéaire de
s'écrit de façon unique comme
combinaison linéaire de ![]() et
et ![]() , alors qu'il existe une infinité de
façons différentes de l'écrire comme combinaison linéaire
de
, alors qu'il existe une infinité de
façons différentes de l'écrire comme combinaison linéaire
de ![]() ,
, ![]() ,
,
![]() et
et
![]() . En effet, considérons par exemple le
vecteur
. En effet, considérons par exemple le
vecteur
![]() . Cette expression constitue l'unique
écriture de
. Cette expression constitue l'unique
écriture de ![]() comme combinaison linéaire de
comme combinaison linéaire de ![]() et
et ![]() .
Par contre, on peut également écrire, pour tout
.
Par contre, on peut également écrire, pour tout
![]() ,
,
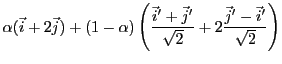
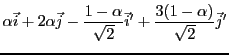
![]() représente le
bon compromis pour écrire les éléments de
représente le
bon compromis pour écrire les éléments de
![]() comme
combinaisons linéaires. C'est ce que l'on appelle une base de
comme
combinaisons linéaires. C'est ce que l'on appelle une base de
![]() ,
en l'occurrence la base canonique de
,
en l'occurrence la base canonique de
![]() .
.
![]()
![]() , la base canonique
de
, la base canonique
de
![]() est la famille constituée des vecteurs
est la famille constituée des vecteurs
![]() , pour
, pour
![]() , le seul
élément non-nul du vecteur étant le
, le seul
élément non-nul du vecteur étant le ![]() -ième.
-ième.
![\begin{theorem}[Th\'eor\\lq eme de la dimension]
Soit $E$\ un $\mathbb{K}$-espac...
...playmath}
\dim_\mathbb{K}(E)
\end{displaymath}
\end{enumerate}
\end{theorem}](img260.png)
![]() est égale à
est égale à ![]() , la base canonique
de
, la base canonique
de
![]() ayant
ayant ![]() éléments.
éléments.
![]() ,
on voit facilement qu'on peut lui enlever un vecteur, la famille résultante
étant maintenant libre, et toujours génératrice.
,
on voit facilement qu'on peut lui enlever un vecteur, la famille résultante
étant maintenant libre, et toujours génératrice.

![]() vecteurs,
et supposons qu'elle soit libre; d'après le théorème de la dimension,
elle peut être complétée pour former une base, mais celle-ci aurait
alors plus de
vecteurs,
et supposons qu'elle soit libre; d'après le théorème de la dimension,
elle peut être complétée pour former une base, mais celle-ci aurait
alors plus de ![]() vecteurs, ce qui est impossible. Donc la famille ne peut
être libre. Considérons maintenant une famille de moins de
vecteurs, ce qui est impossible. Donc la famille ne peut
être libre. Considérons maintenant une famille de moins de ![]() vecteurs,
et supposons qu'elle soit génératrice. On peut alors en extraire une
base, qui aurait alors moins de
vecteurs,
et supposons qu'elle soit génératrice. On peut alors en extraire une
base, qui aurait alors moins de ![]() vecteurs, ce qui est encore une fois
impossible. La famille ne peut donc pas êtretre génératrice.
vecteurs, ce qui est encore une fois
impossible. La famille ne peut donc pas êtretre génératrice.
![]()
![]() un espace vectoriel de dimension
un espace vectoriel de dimension ![]() , et soit
, et soit
![]() une famille libre de
une famille libre de ![]() vecteurs de
vecteurs de ![]() .
Supposons qu'elle ne soit pas génératrice. Alors d'après
le 2) du théorème
.
Supposons qu'elle ne soit pas génératrice. Alors d'après
le 2) du théorème ![[*]](crossref.png) , on peut la compléter pour
former une base de
, on peut la compléter pour
former une base de ![]() . Mais celle-ci a alors plus de
. Mais celle-ci a alors plus de
![]() éléments, ce qui est impossible. Donc la
famille
éléments, ce qui est impossible. Donc la
famille
![]() est nécessairement génératrice.
est nécessairement génératrice.
![]() une famille génératrice
de
une famille génératrice
de ![]() , supposons qu'elle ne soit pas libre. Alors d'après
le 1) du théorème
, supposons qu'elle ne soit pas libre. Alors d'après
le 1) du théorème ![[*]](crossref.png) , on peut lui enlever des
éléments pour obtenir une base, mais celle-ci compte moins de
, on peut lui enlever des
éléments pour obtenir une base, mais celle-ci compte moins de ![]() éléments, ce qui est impossible. Donc la famille
éléments, ce qui est impossible. Donc la famille
![]() est obligatoirement libre.
est obligatoirement libre.

![[*]](crossref.png) l'existence et l'unicité du développement d'un vecteur sur une base:
l'existence et l'unicité du développement d'un vecteur sur une base:
![\begin{theorem}[Unicit\'e du d\'eveloppement sur une base]
Soit $E$\ un espace ...
...c}
x_1\\ x_2\\ \vdots\\ x_n\end{array}\right)
\end{displaymath}
\end{theorem}](img272.png)
![]() (ou
(ou
![]() ), dont on a vu plus haut
la base canonique, il est facile de voir
que les composantes d'un vecteur
), dont on a vu plus haut
la base canonique, il est facile de voir
que les composantes d'un vecteur
![]() dans
cette base canonique ne sont autres que les nombres
dans
cette base canonique ne sont autres que les nombres
![]() .
.
![]() de deux sous-espaces
vectoriels
de deux sous-espaces
vectoriels ![]() et
et ![]() de
de ![]()

![]() et
et ![]() soient deux sous-espaces vectoriels de
soient deux sous-espaces vectoriels de ![]() ,
et soit
,
et soit
![]() . Soit
. Soit
![]() . Alors il existe
. Alors il existe
![]() et
et
![]() tels que
tels que
![]() . Supposons qu'il existe
un autre couple de vecteurs
. Supposons qu'il existe
un autre couple de vecteurs
![]() et
et
![]() tels que
tels que
![]() . Alors on a
. Alors on a
![]() ,
c'est à dire une égalité entre un vecteur de
,
c'est à dire une égalité entre un vecteur de ![]() et un vecteur
de
et un vecteur
de ![]() . A ce point, de deux choses l'une: soit
. A ce point, de deux choses l'une: soit
![]() ,
auquel cas ces deux vecteurs sont nécessairement nuls. Soit
,
auquel cas ces deux vecteurs sont nécessairement nuls. Soit
![]() , et on peut avoir
, et on peut avoir
![]() et
et
![]() . On a donc montré
. On a donc montré

![]() et
et ![]() sont de dimension finie, disons
sont de dimension finie, disons ![]() et
et ![]() , alors ils admettent chacun une base de respectivement
, alors ils admettent chacun une base de respectivement ![]() et
et
![]() élements. L'union de ces deux bases est une famille génératrice
de
élements. L'union de ces deux bases est une famille génératrice
de ![]() , qui est ainsi de dimension inférieure ou égale à
, qui est ainsi de dimension inférieure ou égale à
![]() . Si la somme
. Si la somme ![]() est une somme directe, c'est à dire si
est une somme directe, c'est à dire si
![]() , alors l'union des deux bases est cette fois une base
de
, alors l'union des deux bases est cette fois une base
de ![]() , et la dimension de
, et la dimension de ![]() est alors égale à
est alors égale à ![]() .
On a donc montré
.
On a donc montré
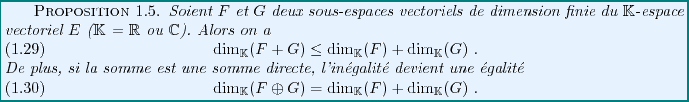

![[*]](crossref.png) ci-dessus, cette égalité
est bien vérifiée.
ci-dessus, cette égalité
est bien vérifiée.

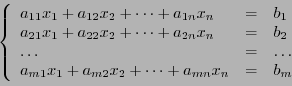
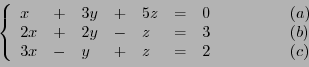
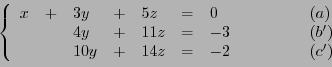
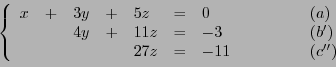
![]() dans la base canonique, cette équation vectorielle peut s'écrire comme
un système de
dans la base canonique, cette équation vectorielle peut s'écrire comme
un système de ![]() équations linéaires, que l'on
peut résoudre par la méthode du pivot.
équations linéaires, que l'on
peut résoudre par la méthode du pivot.
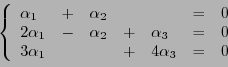
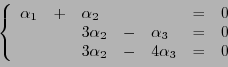
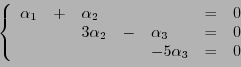
![]() dans (
dans (![[*]](crossref.png) ).
).
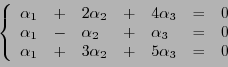
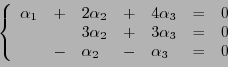
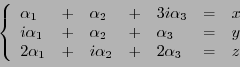
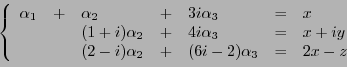
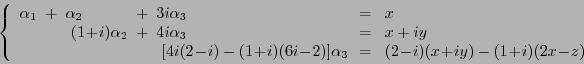
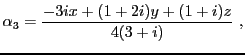
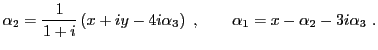
![[*]](crossref.png) (SUITE)
Comment caractériser le sous-espace vectoriel de
(SUITE)
Comment caractériser le sous-espace vectoriel de
![]() engendré
par les vecteurs
engendré
par les vecteurs
![]() ? Il suffit de considérer
un vecteur quelconque
? Il suffit de considérer
un vecteur quelconque