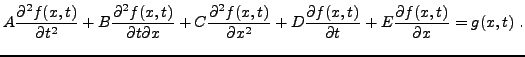La majorité des équations différentielles qui apparaissent
en physique font intervenir des dérivées partielles
par rapport aux variables spatiales et temporelle, et sont
donc des équations aux dérivées partielles.
On se limitera ici aux équations aux dérivées partielles
du second ordre, c'est à dire aux équations de la forme
où les
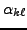 ,
, 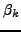 et
et 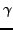 sont des fonctions
fixées.
sont des fonctions
fixées.
Dans le cas d'équations dépendant de deux variables, on distingue
les trois cas suivants:
- Equations hyperboliques: l'exemple classique est l'équation
des ondes
- Equations paraboliques: l'exemple classique est l'équation
de la chaleur
- Equations elliptiques:
l'exemple classique est l'équation de Laplace
Les solutions de ces différentes équations aux dérivées
partielles ont des comportements radicalement différents,
qui correspondent à des situations physiques très différentes
elles aussi.
La classification est basée sur une analogie avec les côniques,
et les considérations suivantes.
Considérons une EDP du second ordre, faisant intervenir deux
variables 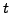 et
et 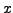 :
:
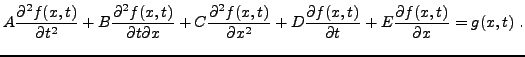 |
(3.1) |
Par analogie avec les côniques, d'équation
cette équation est dite
- Parabolique si
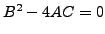 .
.
- Hyperbolique si
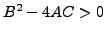 .
.
- Elliptiques si
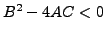 .
.
REMARQUE 3.1 En général, les paramètres
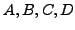
et
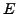
peuvent
être des fonctions de
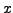
et
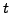
, de sorte que le signe du
discriminant
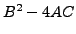
peut varier d'un point
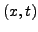
à l'autre, et par là
l'équation changer de régime.
Bruno Torresani
2007-06-26
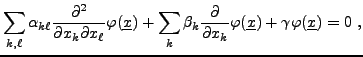
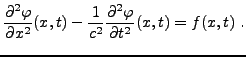
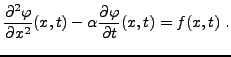
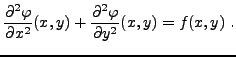
![]() et
et ![]() :
: