Subsections
Avant d'aborder les problèmes elliptiques, il est utile
de s'attarder un peu sur le Laplacien.
L'opérateur Laplacien joue un rôle majeur en Physique. En effet,
il intervient par exemple dans le calcul des variations de
fonctionnelles faisant intervenir la norme carrée du gradient d'une
fonction, ce qui est une situation courante.
Le Laplacien peut prendre différentes formes, suivant le
système de coordonnées utilisé. Par exemple, dans
le cas bidimensionnel, il s'écrit soit en coordonnées
Cartésiennes, soit en coordonnées polaires
(voir la Figure ![[*]](crossref.png) ):
):
Figure:
Systèmes de coordonnées polaires dans le plan.
|
|
Dans le cas tridimensionnel, on peut l'exprimer
en coordonnées Cartésiennes, cylindriques
ou sphériques (voir la Figure ![[*]](crossref.png) ):
):
Figure:
Systèmes de coordonnées cylindriques
et sphériques dans l'espace 3D.
|
|
Il est important de bien comprendre la signification physique
du Laplacien, nous allons l'illustrer dans le cas bidimensionnel.
L'information fondamentale est que le Laplacien d'une fonction de
deux variables 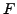 mesure la concavité de
mesure la concavité de 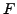 au point considéré. Ainsi:
au point considéré. Ainsi:
- Si
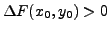 , la fonction
, la fonction 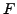 est concave au point
est concave au point
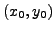 . Donc
. Donc
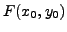 est automatiquement
inférieur à une moyenne de
est automatiquement
inférieur à une moyenne de 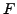 sur un
voisinage de
sur un
voisinage de 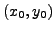 , par exemple un
petit cercle centré sur le point
, par exemple un
petit cercle centré sur le point 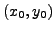 .
.
- Si
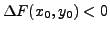 , la fonction
, la fonction 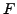 est convexe au point
est convexe au point
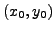 . Donc
. Donc
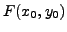 est automatiquement
supérieur à une moyenne de
est automatiquement
supérieur à une moyenne de 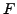 sur un
voisinage de
sur un
voisinage de 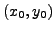 , par exemple un
petit cercle centré sur le point
, par exemple un
petit cercle centré sur le point 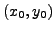 .
.
- Si
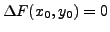 , la fonction
, la fonction 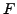 est ``plate'' au point
est ``plate'' au point
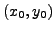 . Donc
. Donc
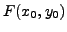 est automatiquement
égal à une moyenne de
est automatiquement
égal à une moyenne de 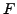 sur un
voisinage de
sur un
voisinage de 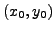 , par exemple un
petit cercle centré sur le point
, par exemple un
petit cercle centré sur le point 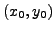 .
.
De là, nous pouvons donner une interprétation simple à un
certain nombre d'équations classiques de la physique.
- L'équation de Laplace
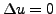 traduit le fait que la solution
traduit le fait que la solution
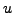 est toujours égale à sa moyenne prise sur un voisinage.
Par exemple, la hauteur d'une membrane attachée par son bord
satisfait l'équation de Laplace. Ceci traduit le fait que la hauteur
de la membrane en un point est toujours égale à la moyenne des
hauteurs sur un petit cercle centré en ce point.
est toujours égale à sa moyenne prise sur un voisinage.
Par exemple, la hauteur d'une membrane attachée par son bord
satisfait l'équation de Laplace. Ceci traduit le fait que la hauteur
de la membrane en un point est toujours égale à la moyenne des
hauteurs sur un petit cercle centré en ce point.
- L'équation de la chaleur
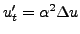 décrit
(entre autres) l'évolution d'un champ de température
(ou de concentration), et peut s'interpréter comme le fait
que la variation de température
décrit
(entre autres) l'évolution d'un champ de température
(ou de concentration), et peut s'interpréter comme le fait
que la variation de température
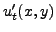 au point de
coordonnées
au point de
coordonnées 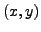 est proportionnelle
est proportionnelle
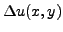 , c'est
à dire à la concavité de la membrane au point de
coordonnées
, c'est
à dire à la concavité de la membrane au point de
coordonnées 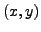 . Ainsi, si
. Ainsi, si 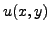 est inférieur
à la moyenne de
est inférieur
à la moyenne de 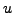 dans un voisinage de
dans un voisinage de 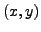 , alors
la température en ce point va augmenter. Inversement, si
, alors
la température en ce point va augmenter. Inversement, si
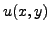 est supérieur à la moyenne de
est supérieur à la moyenne de 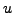 dans un voisinage
de
dans un voisinage
de 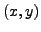 , alors la température en ce point va diminuer.
, alors la température en ce point va diminuer.
- L'équation des ondes
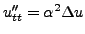 décrit
(entre autres) le déplacement vertical de la membrane d'un tambour,
et peut s'interpréter comme le fait que l'accéleration (ou la
force)
décrit
(entre autres) le déplacement vertical de la membrane d'un tambour,
et peut s'interpréter comme le fait que l'accéleration (ou la
force)
 au point de coordonnées
au point de coordonnées 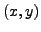 est
proportionnelle
est
proportionnelle
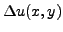 , c'est à dire à la
concavité de la membrane au point de coordonnées
, c'est à dire à la
concavité de la membrane au point de coordonnées 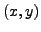 .
Ainsi, si
.
Ainsi, si 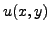 est inférieur à la moyenne de
est inférieur à la moyenne de 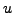 dans
un voisinage de
dans
un voisinage de 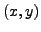 , alors l'accélération (et la force)
est positive.
, alors l'accélération (et la force)
est positive.
On s'intéresse ici à ce que l'on appelle des
problèmes aux bords, c'est
à dire des équations aux dérivées partielles faisant
intervenir des dérivées spatiales, définies dans un domaine
borné, et dans lesquels des conditions aux bords sont
spécifiées. Ce type de problème peut se rencontrer dans
de nombreuses circonstances, par exemple après avoir
éliminé une variable temporelle d'un problème parabolique ou
hyperbolique par séparation des variables.
Les conditions aux bords de Dirichlet spécifient les valeurs
de la solution sur le bord du domaine. L'exemple le plus simple,
en deux dimensions, est fourni par l'équation de Laplace
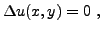 |
(3.7) |
dans un disque 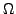 de rayon
de rayon 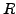 fixé, avec une condition aux bords
fixé, avec une condition aux bords
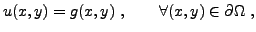 |
(3.8) |
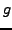 étant une fonction fixée sur
étant une fonction fixée sur
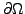 .
On parle alors de problème de Dirichlet intérieur
, par opposition au
problème de Dirichlet extérieur
, dans lequel
on résout (
.
On parle alors de problème de Dirichlet intérieur
, par opposition au
problème de Dirichlet extérieur
, dans lequel
on résout (![[*]](crossref.png) ) dans l'espace extérieur à
) dans l'espace extérieur à
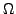 (son complémentaire dans le plan), toujours avec la
condition aux bords (
(son complémentaire dans le plan), toujours avec la
condition aux bords (![[*]](crossref.png) ).
).
Ici, contrairement au cas des conditions aux bords de Dirichlet, on
fixe la valeur de la dérivée normale de la solution
à la frontière du domaine considéré.
La dérivée normale correspond généralement à une quantité
physique appelée le flux: ce qui entre (ou qui sort) du
domaine considéré.
Etant donné le vecteur
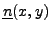 , normal au bord
, normal au bord
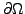 du domaine
du domaine 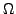 au point
au point
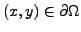 on note
on note
la dérivée normale de 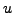 au point
au point 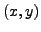 de
de
 .
.
Les conditions de Neumann prennent la forme
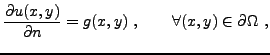 |
(3.9) |
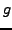 étant une fonction fixée sur
étant une fonction fixée sur
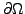 .
On parle alors de problème de Neumann intérieur
, et de
problème de Neumann extérieur
pour le cas complémentaire.
.
On parle alors de problème de Neumann intérieur
, et de
problème de Neumann extérieur
pour le cas complémentaire.
On verra également apparaître des conditions au bord
``mixtes'', faisant intervenir à la fois la valeur de la solution
sur le bord et sa dérivée normale. Ce cas de figure se
présentera notamment dans le cas de l'équation de la chaleur
ci dessous.
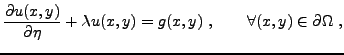 |
(3.10) |
On s'intéresse au problème de Dirichlet intérieur pour
l'équation de Laplace dans un disque de rayon unité. En
coordonnées polaires, le problème est le suivant:
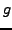 étant une fonction fixée.
étant une fonction fixée.
On utilise la méthode de séparation des variables, et on
recherche des solutions sous la forme
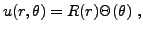 |
(3.13) |
où 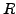 et
et 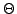 sont des fonctions supposées de classe
sont des fonctions supposées de classe 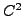 .
.
En reportant cette forme particulière dans l'équation de Laplace,
et en divisant membre à membre par 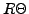 , on obtient
, on obtient
qui s'écrit aussi
Le premier membre étant indépendant de 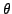 , et le second
étant indépendant de
, et le second
étant indépendant de 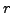 , ils sont tous deux égaux à
une constante, appelée constante de séparation,
que l'on pose égale à
, ils sont tous deux égaux à
une constante, appelée constante de séparation,
que l'on pose égale à 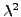 ,
avec
,
avec
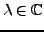 .
Ceci nous conduit au système de deux équations
découplées
.
Ceci nous conduit au système de deux équations
découplées
L'équation angulaire se résout facilement, et donne des solutions
de la forme
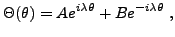 |
(3.16) |
et les contraintes de régularité sur 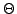 impliquent que
impliquent que
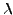 doit être un entier, que l'on peut choisir positif sans
perte de généralité.
doit être un entier, que l'on peut choisir positif sans
perte de généralité.
Passons maintenant à l'équation radiale. Il faut distinguer
deux cas, selon que 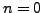 ou
ou 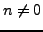 .
.
Si 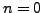 , on a l'équation
, on a l'équation
qui équivaut à l'équation de Sturm-Liouville
simple
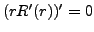 , d'où
, d'où
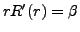 et donc
et donc
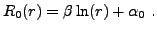 |
(3.17) |
Si l'on veut que la solution soit bornée en 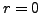 , on doit
nécessairement avoir
, on doit
nécessairement avoir 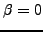 , d'où
, d'où
Si 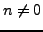 : l'équation prend la forme
: l'équation prend la forme
qui est une équation à coefficients non constants, qui peut être
résolue par la méthode de Fröbenius. Il y a en fait plus simple,
en observant que l'on peut rechercher des solutions sous la forme
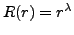 ; en reportant cette forme particulière, on obtient
; en reportant cette forme particulière, on obtient
d'où la solution
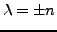 . On vérifie facilement que
. On vérifie facilement que
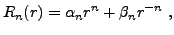 |
(3.18) |
et de nouveau la contrainte
d'avoir une solution bornée implique 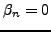 , d'où la solution
, d'où la solution
Les solutions à variables séparées conduisent à une solution
de la forme
pour certaines constantes
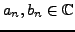 , à déterminer.
, à déterminer.
Il est maintenant temps d'imposer les conditions aux bords:
En posant
on peut remarquer que les coefficients 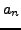 ne sont autres que les
coefficients de Fourier de la fonction
ne sont autres que les
coefficients de Fourier de la fonction 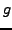
Ceci conclut la solution du problème. Dans le cas un peu plus
général d'un disque de rayon fixé 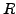 , on montre de même
, on montre de même

EXEMPLE 3.1 Considérons le cas
Alors on voit facilement que
et que la solution est donc donnée par
EXEMPLE 3.2 Considérons le cas
On voit facilement que
et la solution est donc de la forme
Une autre forme de cette solution est donnée par la formule
intégrale de Poisson
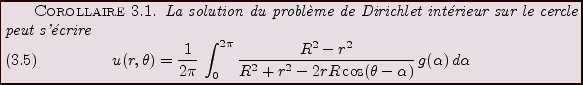
Preuve:
Il suffit de reporter les coefficients de Fourier à l'intérieur de
la solution trouvée:
d'où on déduit le résultat par simplification.
Le problème extérieur
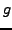 étant une fonction fixée.
peut être résoilmu de façon tout à
fait similaire. Les solutions générales
angulaire (
étant une fonction fixée.
peut être résoilmu de façon tout à
fait similaire. Les solutions générales
angulaire (![[*]](crossref.png) ) et
radiale (
) et
radiale (![[*]](crossref.png) ) et (
) et (![[*]](crossref.png) )
sont toujours valides. L'exigence d'une solution bornée
impose encore la nullité du coefficient du terme
logarithmique dans (
)
sont toujours valides. L'exigence d'une solution bornée
impose encore la nullité du coefficient du terme
logarithmique dans (![[*]](crossref.png) ), mais impose
cette fois la nullité des coefficients des termes en
), mais impose
cette fois la nullité des coefficients des termes en 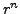 dans (
dans (![[*]](crossref.png) ), ce qui conduit à des solutions
de la forme
), ce qui conduit à des solutions
de la forme
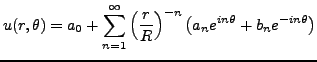 |
(3.21) |
où les coefficients sont toujours donnés
par (![[*]](crossref.png) ).
).
Bruno Torresani
2007-06-26
![[*]](crossref.png) ):
):
![[*]](crossref.png) ):
):
![]() mesure la concavité de
mesure la concavité de ![]() au point considéré. Ainsi:
au point considéré. Ainsi:
![[*]](crossref.png) ) dans l'espace extérieur à
) dans l'espace extérieur à
![[*]](crossref.png) ).
).
![]() , normal au bord
, normal au bord
![]() du domaine
du domaine ![]() au point
au point
![]() on note
on note

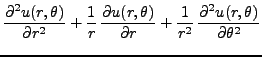
![]() , on obtient
, on obtient
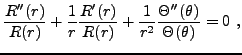
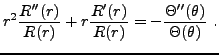
![]() , on a l'équation
, on a l'équation
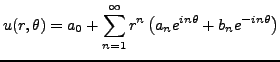
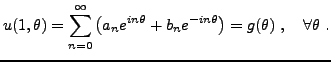
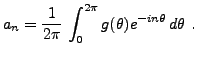

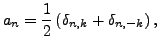
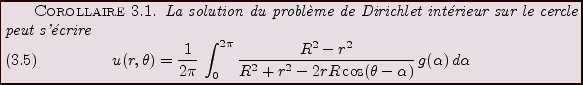
![$\displaystyle \frac1{2\pi}\left[
\int_0^{2\pi}\!\!\!\!g(\alpha)\,d\alpha +
\sum...
... \int_0^{2\pi}\!\!\!\!\!\!e^{-in(\theta-\alpha)}g(\alpha)d\alpha\right)
\right]$](img711.png)
![$\displaystyle \frac1{2\pi}\int_0^{2\pi}
\left[1 + \sum_{n=1}^\infty\left(\frac{...
...{in(\theta-\alpha)} +
e^{-in(\theta-\alpha)}\right)\right] \,g(\alpha)\,d\alpha$](img712.png)
![$\displaystyle \frac1{2\pi}\int_0^{2\pi}
\left[ 1 + \frac1{1-re^{i(\theta-\alpha)}/R} +
\frac1{1-re^{-i(\theta-\alpha)}/R} -2\right]
\,g(\alpha)\,d\alpha\ ,$](img713.png)
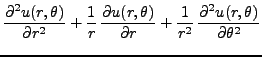
![[*]](crossref.png) ) et
radiale (
) et
radiale (![[*]](crossref.png) ) et (
) et (![[*]](crossref.png) )
sont toujours valides. L'exigence d'une solution bornée
impose encore la nullité du coefficient du terme
logarithmique dans (
)
sont toujours valides. L'exigence d'une solution bornée
impose encore la nullité du coefficient du terme
logarithmique dans (![[*]](crossref.png) ), mais impose
cette fois la nullité des coefficients des termes en
), mais impose
cette fois la nullité des coefficients des termes en ![[*]](crossref.png) ), ce qui conduit à des solutions
de la forme
), ce qui conduit à des solutions
de la forme
![[*]](crossref.png) ).
).