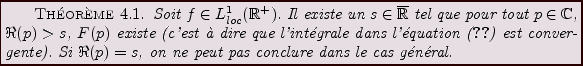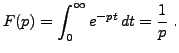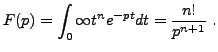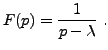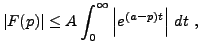Définition et premières propriétés
Il est utile d'introduire à ce point la notion de fonction
localement intégrable.

![\begin{definition}[Transformation de Laplace]
La transform\'ee de Laplace d'une ...
...) e^{-pt} dt\ ,
\end{equation}quand cette int\'egrale converge.
\end{definition}](img877.png)
La variable
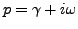 est une variable complexe.
Le domaine des valeurs de
est une variable complexe.
Le domaine des valeurs de 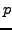 pour lesquelles cette intégrale est convergente pose déjà
quelques problèmes. Deux remarques importantes sont à faire.
pour lesquelles cette intégrale est convergente pose déjà
quelques problèmes. Deux remarques importantes sont à faire.
- L'intégrabilité de
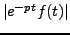 ne dépend
pas de
ne dépend
pas de 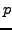 lui même, mais seulement de sa partie réelle
lui même, mais seulement de sa partie réelle
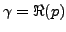 .
.
- Si pour un certain
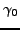 , la fonction
, la fonction
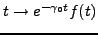 est intégrable, alors
est intégrable, alors
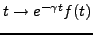 est elle aussi intégrable
pour tout
est elle aussi intégrable
pour tout
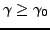 .
.
Ceci nous conduit au résultat suivant:
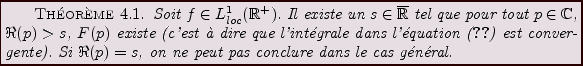
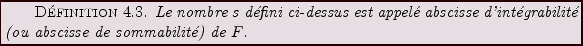
Il est utile de considérer quelques exemples.
-
 (la fonction de Heaviside);
alors
(la fonction de Heaviside);
alors 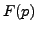 est bien définie pour
est bien définie pour 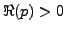 :
l'intégrale est convergente (par contre, l'intégrale n'est pas
absolument convergente pour
:
l'intégrale est convergente (par contre, l'intégrale n'est pas
absolument convergente pour 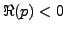 ).
Donc
).
Donc 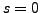 ; et si
; et si 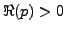 , on a
, on a
Notons que la fonction
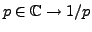 est bien définie pour
tout
est bien définie pour
tout
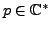 ; cependant, elle n'est la transformée de
Laplace de la fonction
; cependant, elle n'est la transformée de
Laplace de la fonction 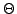 que dans le demi-plan
que dans le demi-plan
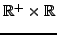 , domaine de définition de cette dernière.
, domaine de définition de cette dernière.
-
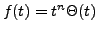 : de nouveau,
: de nouveau, 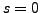 . Si
. Si 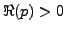 , on a
, on a
-
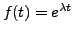 , où
, où
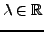 . L'intégrale définissant
. L'intégrale définissant
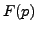 est convergente dès que
est convergente dès que
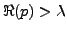 . Donc
. Donc 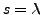 , et
si
, et
si 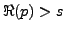 , on voit immédiatement que
, on voit immédiatement que
-
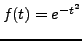 ; alors l'intégrale définissant
; alors l'intégrale définissant 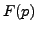 est
convergente quel que soit
est
convergente quel que soit
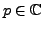 , et par conséquent
, et par conséquent 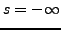 .
.
-
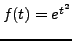 ; alors l'intégrale définissant
; alors l'intégrale définissant 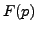 n'est
jamais convergente, et donc
n'est
jamais convergente, et donc 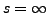 .
.
Plus généralement, on utilise souvent le critère suivant qui donne une
condition suffisante pour l'existence de la transformée de Laplace.

La preuve est immédiate:
il suffit d'insérer l'estimation précédente dans la
définition de la transformée de Laplace, et de voir que
qui converge dès que 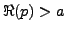 .
.
Les hypothèses faites dans cette dernière proposition sont
suffisamment générales pour couvrir un grand nombre de
cas d'intérêt.
Bruno Torresani
2007-06-26

![\begin{definition}[Transformation de Laplace]
La transform\'ee de Laplace d'une ...
...) e^{-pt} dt\ ,
\end{equation}quand cette int\'egrale converge.
\end{definition}](img877.png)