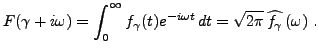Propriétés élémentaires
La transformation de Laplace possède un certain nombre
de propriétés simples, conséquences directes de la définition.
Nous donnons ci-dessous les plus simples.
- Linéarité: Si
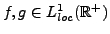 ont pour transformées
de Laplace respectives
ont pour transformées
de Laplace respectives 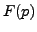 et
et 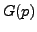 , et abscisses d'intégrabilité
, et abscisses d'intégrabilité
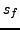 et
et 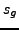 , soit
, soit  la fonction définie par
la fonction définie par
 . Alors
. Alors
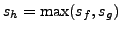 si
si
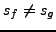 , et
, et
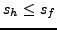 si
si 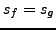 .
De plus, si
.
De plus, si 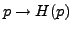 est la TL de
est la TL de  , alors
, alors
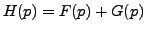 .
.
- Translation: Soit
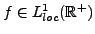 ,
d'abscisse d'intégrabilité
,
d'abscisse d'intégrabilité 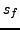 , et soit
, et soit 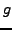 définie par
définie par
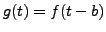 , où
, où
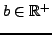 . Alors
. Alors
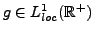 a pour abscisse d'intégrabilité
a pour abscisse d'intégrabilité 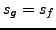 , et sa transformée
de Laplace est donnée par
, et sa transformée
de Laplace est donnée par
- Modulation: Soit
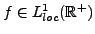 ,
d'abscisse d'intégrabilité
,
d'abscisse d'intégrabilité 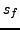 , et soit
, et soit 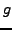 définie par
définie par
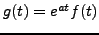 , où
, où
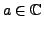 . Alors
. Alors
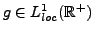 a pour abscisse d'intégrabilité
a pour abscisse d'intégrabilité
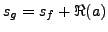 , et sa
transformée de Laplace est donnée par
, et sa
transformée de Laplace est donnée par
- Lien avec la transformation de Fourier: Soit
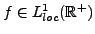 , d'abscisse d'intégrabilité
, d'abscisse d'intégrabilité
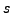 et soit
et soit 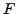 sa transformée de Laplace. Pour tout
sa transformée de Laplace. Pour tout
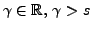 , soit
, soit
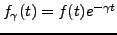 . Alors, on a
pour
. Alors, on a
pour
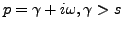 :
:
Cette dernière propriété va jouer un rôle important dans
le problème d'inversion de la transformation de Laplace.
Bruno Torresani
2007-06-26