Next: La méthode de Frobenius Up: Equations différentielles Previous: Equations différentielles
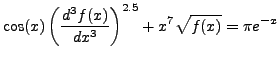
est très probablement difficile à résoudre explicitement. L'une des raisons est que cette équation différentielle est non-linéaire; ainsi, étant donnée une solution

Il est facile de démontrer que des combinaisons linéaires
de solutions d'une équation différentielle linéaire homogène
sont toujours solutions de cette équation. En fait, on montre le
résultat fondamental suivant
![]()
Ainsi, une équation différentielle de ce type est loin d'admettre
une unique solution. L'unicité peut être retrouvée en imposant
des conditions supplémentaires.
Dans le cas d'une équation d'ordre ![]() , on a besoin de
, on a besoin de ![]() équations
linéaires supplémentaires pour spécifier une solution unique.
Ceci est généralement effectué en imposant des conditions aux
bords, ou conditions aux limites
.
équations
linéaires supplémentaires pour spécifier une solution unique.
Ceci est généralement effectué en imposant des conditions aux
bords, ou conditions aux limites
.
Les équations homogènes jouent en fait un rôle fondamental.
En effet, considérons une équation différentielle linéaire
inhomogène, comme en (![[*]](crossref.png) ), et soient
), et soient
![]() et
et ![]() deux solutions de cette équation. On voit alors facilement
que
deux solutions de cette équation. On voit alors facilement
que ![]() est solution de l'équation
différentielle homogène
est solution de l'équation
différentielle homogène
![[*]](crossref.png) ),
on peut lui ajouter n'importe quelle solution de l'équation
homogène correspondante, le résultat étant toujours
solution de (
),
on peut lui ajouter n'importe quelle solution de l'équation
homogène correspondante, le résultat étant toujours
solution de (![[*]](crossref.png) ). On a donc montré
). On a donc montré

L'équation homogène correspondante s'écrit sous la forme
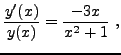
et s'intègre facilement, pour donner
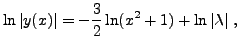
d'où la solution générale de l'équation homogène
Par ailleurs, une solution apparente (à défaut d'être évidente) de l'équation inhomogène est donnée par
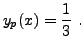
On en déduit la solution générale de l'équation inhomogène
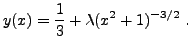
On obtient en fait une famille à un paramètre de solutions.
qui se résout par la méthode des radicaux. Dans ce cas, les racines sont de la forme
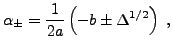
où
qui engendrent bien l'espace vectoriel de dimension 2 des solutions de l'équation. La solution générale est alors de la forme
les constantes
Le cas limite ![]() est un peu plus complexe. En effet, il y a dans
ce cas une seule racine
est un peu plus complexe. En effet, il y a dans
ce cas une seule racine
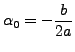
à l'équation caractéristique, qui ne fournit qu'une seule solution de l'équation homogène
Or on sait d'après le Théorème
![[*]](crossref.png) qu'il
existe deux solutions linéairement indépendantes de l'équation
de départ (puisqu'elle est du second ordre). On verra un peu plus loin
une méthode (basée sur le Wronskien,
permettant d'obtenir une seconde solution. Dans notre cas, cette
approche se simplifie, et revient à rechercher une
seconde solution, sous la forme particulière
qu'il
existe deux solutions linéairement indépendantes de l'équation
de départ (puisqu'elle est du second ordre). On verra un peu plus loin
une méthode (basée sur le Wronskien,
permettant d'obtenir une seconde solution. Dans notre cas, cette
approche se simplifie, et revient à rechercher une
seconde solution, sous la forme particulière
Comme
![[*]](crossref.png) ), en insérant la forme particulière
de
), en insérant la forme particulière
de ![[*]](crossref.png) ), on aboutit à une nouvelle équation
que doit satisfaire
), on aboutit à une nouvelle équation
que doit satisfaire
soit en insérant la forme particulière de
d'où
Ainsi, on obtient la solution générale de l'équation
![[*]](crossref.png) , dans le cas particulier
, dans le cas particulier
Considérons une équation linéaire d'ordre ![]() comme
en (
comme
en (![[*]](crossref.png) ), et supposons que l'on ait déjà
obtenu la solution générale de l'équation
homogène (
), et supposons que l'on ait déjà
obtenu la solution générale de l'équation
homogène (![[*]](crossref.png) ), celle-ci engendrant un espace
de dimension
), celle-ci engendrant un espace
de dimension ![]() . La solution générale s'écrit alors
comme combinaison linéaire de
. La solution générale s'écrit alors
comme combinaison linéaire de ![]() ``solutions élementaires''
``solutions élementaires''
La méthode de Laplace revient à rechercher une solution particulière de (
![[*]](crossref.png) ) comme combinaison des solutions
) comme combinaison des solutions
En insérant cette forme dans l'équation inhomogène (
![[*]](crossref.png) ), on aboutit à une nouvelle
équations différentielle, impliquant uniquement les
fonctions
), on aboutit à une nouvelle
équations différentielle, impliquant uniquement les
fonctions
On ne traitera pas ici le cas général, et on se limitera aux
cas ![]() ou
ou ![]() .
.
Dans le cas ![]() , partant d'une équation
, partant d'une équation
partons d'une solution
d'où la solution
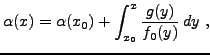
d'où on déduit la solution de l'équation inhomogène. Reprenons l'exemple précédent.
EXEMPLE ![[*]](crossref.png) (SUITE).
Dans ce cas, on recherche une solution sous la forme
(SUITE).
Dans ce cas, on recherche une solution sous la forme
On a alors, compte tenu du fait que
Imposer que
d'où
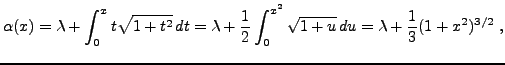
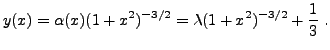
Le cas des équations du second ordre est un peu plus complexe, car
l'espace vectoriel engendré par les solutions de l'équation
homogène est de dimension 2. On peut alors imposer une condition
supplémentaire sur ![]() et
et ![]() . On choisit en général
. On choisit en général
arbitraire... mais efficace.
Partons d'une équation de la forme
considérons deux solutions
On a alors
compte tenu de la condition supplémentaire imposée, et donc
En insérant cela dans l'équation de départ, on aboutit pour tout
Le déterminant de ce système, appelé Wronskien,

est non nul, donc il existe une unique solution
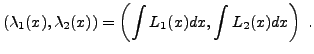
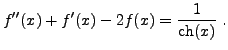
L'équation homogène est à coefficients constants, et se prête donc bien à des solutions sous forme d'exponentielles. L'équation caractéristique
admet les deux racines
On utilise maintenant la variation de la constante. La condition supplémentaire prend ici la forme
d'où on tire
En reportant cela dans l'autre équation, on obtient
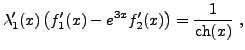
c'est à dire
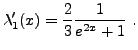
On a donc
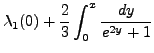 |
|||
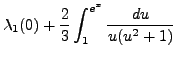 |
|||
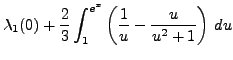 |
|||
![$\displaystyle \lambda_1(0) + \left[\frac{2}3 \ln \vert u\vert -
\frac1{3}\ln (u^2+1)\right]_1^{e^x}$](img370.png) |
|||
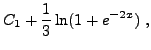 |
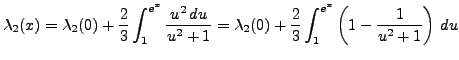
d'où on déduit
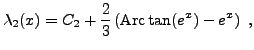
pour une certaine constante
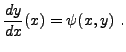
Dans les cas où
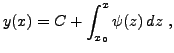
où
On se limite aux équations du pemier ordre linéaires.
La forme la plus générale est
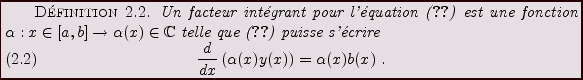
Dans ces conditions, la solution de (![[*]](crossref.png) )
est explicite:
)
est explicite:
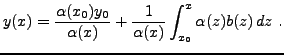 |
(2.4) |
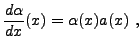
de sorte que la solution est (en fixant la constante multiplicative pour que
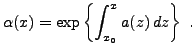 |
(2.5) |
avec la condition
(donc
![$\displaystyle y(x) = e^{-(x^2-x_0^2)/2}\left[y_0 +
\int_{x_0}^x z e^{(z^2-x_0^2)/2}\,dz\right]
= 1 + (y_0-1)e^{-(x^2-x_0^2)/2}\ .
$](img394.png)

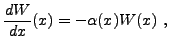
de sorte que sa forme est
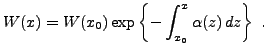 |
(2.6) |
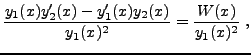
d'où
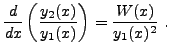
On en déduit par intégration
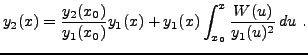 |
(2.7) |
Bruno Torresani 2007-06-26