Equations différentielles

Les équations différentielles et les équations aux dérivées partielles constituent une composante fondamentale de la physique, dans la mesure où elles sont utiles pour décrire de nombreux systèmes physiques. On se limitera ici à certaines classes d'équations différentielles qui admettent des solutions relativement simples à obtenir.

Dans le cas de fonctions d'une variable réelle, une équation différentielle d'ordre $n$ d'indéterminée $f$ est une relation de la forme

$$F(x,f(x),f'(x),\dots f^{(n)}(x)) = 0\ ,$$

où on a noté $f^{(n)}$ la dérivée $n$ -ième de $f$ :

$$f^{(n)}(x) = \frac{d^nf}{dx^n}(x)\ .$$

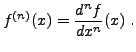
Résoudre une équation différentielle revient à trouver toutes ses solution.

Une solution d'une équation différentielle définit dans un repère (généralement choisi orthonormé) une courbe, appelée courbe intégrale de l'équation. Résoudre l'équation revient donc à déterminer la courbe intégrale correspondante.