Subsections
Applications Linéaires
On rappelle qu'une application
d'un ensemble  vers un ensemble
vers un ensemble  associe à tout élément
associe à tout élément
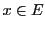 un élément
un élément
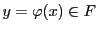 .
.
La notion fondamentale de ce chapitre est la notion d'application
linéaire. Une application linéaire d'un espace vectoriel vers un autre
est une application qui préserve l'addition et la
multiplication scalaire. Plus précisément:

EXEMPLE 3.1 Soient
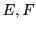
deux
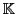
-espaces vectoriels. Soit
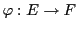
l'application définie par
(
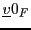
étant le vecteur nul dans

). Il est facile de vérifier que

est une application linéaire.
EXEMPLE 3.2 Soit

un
-espace vectoriel. Soit
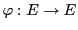
l'application
définie par
Il est facile de vérifier que

est une application linéaire,
appelée
application identité,
et notée
EXEMPLE 3.3 Soit
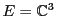
, et soit
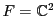
. Soit
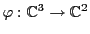
, définie par
Vérifions que

est une application linéaire. Calculons
ce qui montre la première égalité. De plus,
ce qui achève la démonstration.
EXEMPLE 3.4 Soit
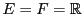
et soit

définie par
Il est manifeste que

n'est pas une application linéaire.
De même, les applications
ne sont pas des applications linéaires (au moins tant que
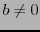
dans le cas e la première).
EXEMPLE 3.5 On considère l'ensemble
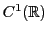
des applications
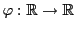
dérivables à dérivée continue, et l'ensemble
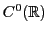
des applications
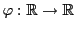
continues.
Il est possible de démontrer que
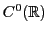
et
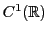
sont des espaces vectoriels: ce sont des sous-ensembles
de
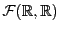
, dont on a déjà vu qu'il était
un

-espace vectoriel. De plus, la somme de deux fonctions continues est
continue, tout comme le produit d'une fonction continue par un réel.
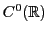
est donc un sous-espace vectoriel de
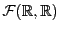
, et
par conséquent c'est un

-espace vectoriel. On montre de même
que
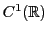
est donc un sous-espace vectoriel de
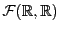
, et
donc un

-espace vectoriel.
Soit 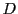 l'application qui à
l'application qui à
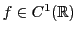 associe sa dérivée
(qui est donc une fonction continue)
associe sa dérivée
(qui est donc une fonction continue)
On sait que
donc
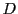
est une application linéaire.
Un cas particulier d'application linéaire est fourni par les
projections. Soit  un espace vectoriel,
et soient
un espace vectoriel,
et soient  et
et 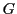 deux sous-espaces vectoriels supplémentaires
dans
deux sous-espaces vectoriels supplémentaires
dans  :
:
Alors, on sait que pour tout
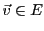 , il existe un unique
, il existe un unique
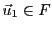 et un unique
et un unique
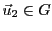 tels que
tels que
L'application qui associe à tout
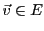 le vecteur
le vecteur
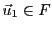 est appelée projection de
est appelée projection de  sur
sur  , parallèlement
à
, parallèlement
à 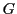 .
.
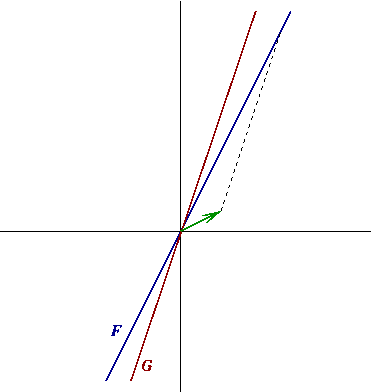
EXEMPLE 3.6 Prenons
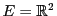
, et soient

et
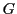
sont tous deux de dimension 1; une base de

est
constituée par le vecteur
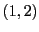
, et une base de
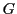
est
constituée par le vecteur
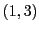
.
Pour tout
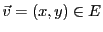 , on sait donc qu'il existe un unique couple
de réels
, on sait donc qu'il existe un unique couple
de réels
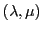 tel que
tel que
Un calcul explicite montre que
Soit maintenant
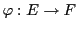
associant à
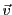
le vecteur
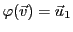
. On a alors
Notons que l'on a aussi
Figure:
Projection sur  parallèlement à
parallèlement à  .
.
 |

Soit  un espace vectoriel de dimension
un espace vectoriel de dimension  , et soit
, et soit
une base de  . On a déjà vu que tout vecteur
. On a déjà vu que tout vecteur
 peut se décomposer de façon unique comme combinaison linéaire
des vecteurs de la base
peut se décomposer de façon unique comme combinaison linéaire
des vecteurs de la base
Ceci permet d'associer à 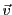 sa matrice (colonne) dans la base
sa matrice (colonne) dans la base
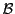 ,
notée
,
notée
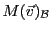 ou plus simplement (lorsqu'il n'y a pas de
confusion possible)
ou plus simplement (lorsqu'il n'y a pas de
confusion possible)
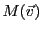 :
:
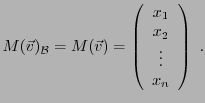 |
(3.1) |
Il est évident que la matrice d'un vecteur dépend de la base
choisie. On verra plus loin comment la matrice est modifiée
lorsque l'on change de base.
On va maintenant voir que les matrices s'introduisent aussi naturellement
dans le cadre de l'étude des applications linéaires, dès
lors que l'on a choisi une base dans chacun des espaces vectoriels
concernés. En effet, soient  et
et  deux
deux
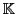 -espaces vectoriels,
avec
-espaces vectoriels,
avec 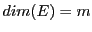 et
et 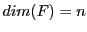 ,
et soit
,
et soit
une application linéaire.
Soit
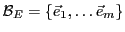 une base de
une base de  , et soit
, et soit
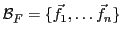 une base de
une base de  .
.
Pour tout
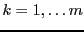 , on sait que
, on sait que
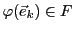 . Donc,
. Donc,
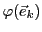 admet une unique décomposition en combinaison
linéaire de la base
admet une unique décomposition en combinaison
linéaire de la base
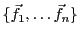 de
de  : il existe
une unique famille de scalaires
: il existe
une unique famille de scalaires
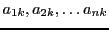 telle que
telle que
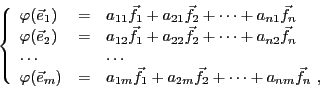 |
(3.2) |
que l'on synthétise sous la forme d'une équation générique
Ces scalaires
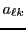 peuvent se mettre sous la forme d'une
matrice
peuvent se mettre sous la forme d'une
matrice
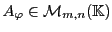 .
.

REMARQUE 3.1 Il existe une façon simple d'écrire cette matrice. Partant
du système (
![[*]](crossref.png)
), on peut écrire les matrices
colonne des images
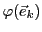
dans la base
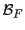
:
Ainsi, la matrice
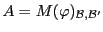
s'obtient en mettant côte
à côte ces matrices colonnes.
EXEMPLE 3.7 Considérons le cas
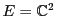
, et soit
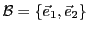
la
base canonique de

:
Soit

la projection de

sur le sous-espace vectoriel
engendré par
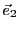
, parallèlement à
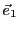
.
Alors
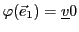
et
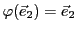
.
La matrice de

dans la base canonique
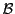
est donc
EXEMPLE 3.8 On considère l'application linéaire
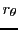
, qui à tout
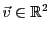
associe le vecteur obtenu à partir de
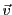
par
rotation d'angle
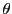
. On a alors
La matrice de l'application linéaire
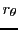
dans la base canonique
est la matrice
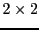
que nous avons déjà rencontrée.
Quelle est l'utilité des matrices dans ce contexte ?
le calcul matriciel permet de calculer directement les coordonnées
par rapport à une base
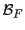 de
de  de l'image d'un vecteur
de l'image d'un vecteur
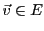 , connaissant ses composantes par rapport à une base
, connaissant ses composantes par rapport à une base
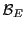 de
de  .
.

Preuve:
Supposons que  soit de dimension
soit de dimension 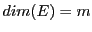 , et
que
, et
que  soit de dimension
soit de dimension 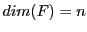 .
Soit
.
Soit
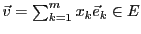 . La linéarité de
l'application
. La linéarité de
l'application  donne
donne
Si on note
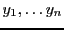 les composantes de
les composantes de
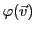 dans la base de
dans la base de  , c'est à dire
, c'est à dire
on obtient bien par identification
ce qui est bien le produit matriciel annoncé.
Notons que dans ce cas, la matrice colonne
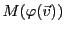 est
une matrice à
est
une matrice à  lignes, la matrice
lignes, la matrice
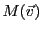 est une matrice
à
est une matrice
à 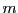 lignes, et donc la matrice
lignes, et donc la matrice
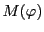 est une matrice
à
est une matrice
à  lignes et
lignes et 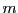 colonnes. On a bien, conformément aux règles
du calcul matriciel
colonnes. On a bien, conformément aux règles
du calcul matriciel
EXEMPLE ![[*]](crossref.png) (SUITE)
Reprenons l'exemple de la rotation ci-dessus. Soit
(SUITE)
Reprenons l'exemple de la rotation ci-dessus. Soit
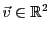 , et soit
, et soit
sa matrice dans la base canonique. On a donc
et donc
Le calcul donne
et on vérifie facilement que
EXEMPLE 3.9 Soient
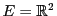
et
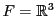
, munis de leurs bases canoniques respectives
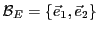
et
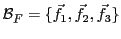
(on rappelle que
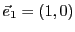
et
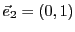
, alors que
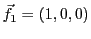
,
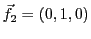
et
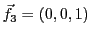
).
Soit
On voit facilement que
et donc la matrice de

par rapport à ces deux bases vaut
On vérifie facilement que pour tous
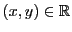
,
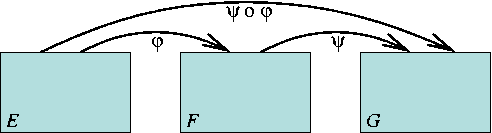
La relation étroite entre les applications linéaires et le
produit matriciel apparaît plus clairement grâce au résultat
fondamental suivant, qui exprime la matrice de la composée de deux
applications linéaires (voir FIG. ![[*]](crossref.png) ci dessous)
en fonction de leurs matrices
ci dessous)
en fonction de leurs matrices
Figure:
Composition de deux applications linéaires.
 |
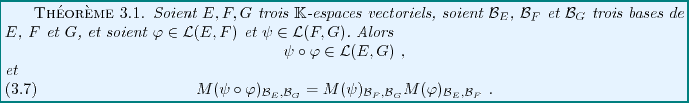
Preuve:
Soit
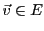 , et soit
, et soit
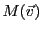 sa matrice colonne. Par
l'associativité du produit matriciel, on a
sa matrice colonne. Par
l'associativité du produit matriciel, on a
Mais on a aussi
d'où on déduit le résultat.
EXEMPLE 3.10 Dans
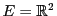
, on considère les deux applications linéaires suivantes:
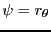
, la rotation d'angle
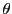
autour de l'origine,
et

, définie par
On a donc
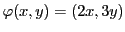
. Calculons
On a donc
de sorte que la matrice de
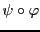
vaut
On vérifie bien de plus que
Supposons que
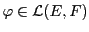 soit une application linéaire
de
soit une application linéaire
de  dans
dans  . Etant données deux bases de
. Etant données deux bases de  et
et  respectivement, on a vu que l'on peut associer à
respectivement, on a vu que l'on peut associer à  sa matrice par rapport à ces deux bases.
sa matrice par rapport à ces deux bases.
Supposons maintenant que  soit bijective.
Alors il existe
soit bijective.
Alors il existe
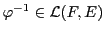 telle que
telle que
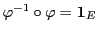 .
Dans ce cas, on peut associer à
.
Dans ce cas, on peut associer à
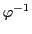 une matrice, qui
est reliée à
une matrice, qui
est reliée à
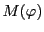 . Plus précisément, on a:
. Plus précisément, on a:

Preuve:
Supposons que
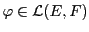 soit bijective. Alors on sait que
soit bijective. Alors on sait que
et donc
(où
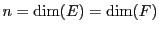 ). De même,
). De même,
et donc
On en déduit donc que
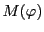 est inversible, et que
est inversible, et que
Réciproquement, supposant que
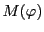 est inversible, on
en déduit de façon similaire que
est inversible, on
en déduit de façon similaire que  est nécessairement
un isomorphisme.
est nécessairement
un isomorphisme.
REMARQUE 3.2 Comment calcule-t-on l'inverse d'une matrice ?
Le calcul de l'inverse d'une matrice carrée peut se ramener
à la résolution d'un système linéaire, à autant
d'équations que d'inconnues. Si celui possède une solution,
on montre qu'elle est unique, et la matrice est alors inversible.
Prenons l'exemple de la matrice 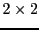
Si

est inversible, alors
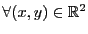
, il existe
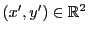
tel que
Ceci équivaut au système de deux équations à deux inconnues
qui admet pour solution
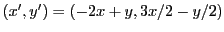
, qui se met
sous forme matricielle
d'où on déduit

EXEMPLE 3.11 Soit
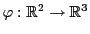
, définie par
On voit alors facilement que
Cet ensemble est en fait un sous-espace vectoriel de dimension
2 de
. On vérifie en effet qu'il n'est pas vide, et qu'il
est stable par addition et multiplication scalaire.
Il s'agit d'un plan vectoriel dans
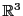 .
.
Cette propriété est en fait une propriété générique
de l'image d'une application linéaire.

Preuve:
La première propriété est une conséquence de la seconde, qu'il suffit
donc de démontrer. Pour cela, soient
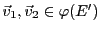 . Alors
il existe
. Alors
il existe
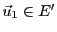 et
et
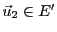 tels que
tels que
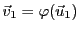 , et
, et
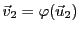 . Donc,
. Donc,
d'après la linéarité de  .
. 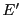 étant un sous-espace vectoriel
de
étant un sous-espace vectoriel
de  ,
,
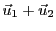 appartient donc à
appartient donc à 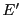 , et
, et
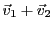 est donc l'image par
est donc l'image par  d'un élément de
d'un élément de 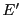 .
Donc,
.
Donc,
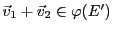 .
.
Soit maintenant
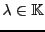 . On a
. On a
et comme
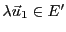 , on a donc bien
, on a donc bien
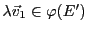 ,
ce qui conclut la démonstration.
,
ce qui conclut la démonstration.

EXEMPLE 3.12 Soit
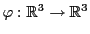
, définie par
Soit
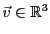
. On a
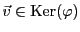
si
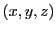
vérifie
Ce système se résout facilement, par exemple par la méthode
du pivot de Gauss, et on voit facilement que
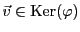
si et seulement si
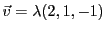
pour un certain
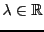
. Ceci définit en fait un sous-espace vectoriel
de dimension 1 de
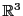
.

Preuve:
Soient
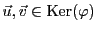 ; alors
; alors
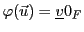 et
et
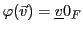 . Donc
. Donc
De plus, pour tout
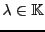 ,
,
ce qui conclut la preuve.

Preuve:
Supposons que  soit injective. Alors, comme
soit injective. Alors, comme
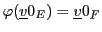 ,
,
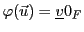 implique nécessairement
que
implique nécessairement
que
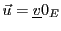 . Réciproquement, supposons que
. Réciproquement, supposons que
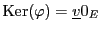 ,
et soient
,
et soient
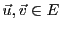 tels que
tels que
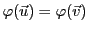 .
Alors par linéarité de
.
Alors par linéarité de  , on a
, on a
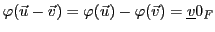 , d'où
, d'où
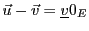 , et donc
, et donc
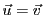 .
.

Preuve:
- Supposons que
 soit injective, que
soit injective, que
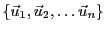 soit une famille libre de vecteurs de
soit une famille libre de vecteurs de  , et qu'il existe
, et qu'il existe
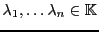 tels que
tels que
Alors, par linéarité de  , ceci est équivalent à
, ceci est équivalent à
qui implique
par injectivité de  , et donc
, et donc
car la famille
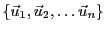 est libre. Ceci
démontre le premier point.
est libre. Ceci
démontre le premier point.
- Supposons que
 soit surjective, et que
soit surjective, et que
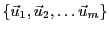 soit une famille génératrice de
soit une famille génératrice de  . Alors
. Alors
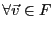 , il existe
, il existe
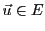 tel que
tel que
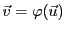 . De plus, il existe
. De plus, il existe
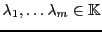 tels que
tels que
de sorte que l'on a, par linéarité de 
Ceci prouve le second point.
- Si
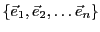 est une base de
est une base de  , c'est donc
une famille libre et génératrice. Si
, c'est donc
une famille libre et génératrice. Si  est bijective,
est bijective,
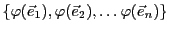 est elle
aussi libre et génératrice, et c'est donc une base de
est elle
aussi libre et génératrice, et c'est donc une base de  .
.
REMARQUE 3.3 On dit que deux espaces vectoriels sont
isomorphes
si il
existe un isomorphisme entre eux. Une conséquence importante de
ce résultat est que
deux espaces vectoriels de dimension finie
isomorphes sont nécessairement de même dimension.
![\begin{theorem}[Th\'eor\\lq eme du rang (ou de la dimension)]
Soient $E$\ et $F$\ d...
...(E) = {\rm rg}(\varphi) + dim({\rm Ker}(\varphi))
\end{displaymath}\end{theorem}](img794.png)
EXEMPLE 3.13 Reprenons l'exemple de l'application linéaire
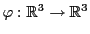
, définie par
On a vu plus haut que
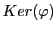
est un sous-espace
vectoriel de
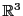
de dimension 1. On peut donc en déduire que
le rang de

est égal à deux, que que l'on va vérifier.
Soit
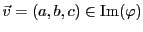 . Il existe
. Il existe
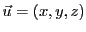 tel que
tel que
Ce système est équivalent au système
qui n'admet de solution que si
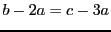
, c'est à dire
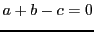
.
Ainsi, on a montré que
qui est bien un sous-espace vectoriel de dimension 2 de
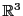
.
Dans ces conditions, on peut déduire du résultat ci-dessus

Preuve:
Il suffit de démontrer que les deux premières assertions
sont équivalentes. Supposons tout d'abord que  soit
injective. Alors
soit
injective. Alors
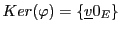 , est donc de dimension nulle.
Par conséquent,
, est donc de dimension nulle.
Par conséquent,
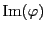 étant un sous-espace vectoriel de
étant un sous-espace vectoriel de  , il est
alors nécessairement égal à
, il est
alors nécessairement égal à  , d'où
, d'où  est
surjective.
est
surjective.
Inversement, supposons que  soit surjective. Alors
soit surjective. Alors
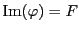 , d'où on déduit, par les mêmes
arguments, que
, d'où on déduit, par les mêmes
arguments, que
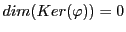 , d'où
, d'où  est
nécessairement injective.
est
nécessairement injective.
On a déjà vu que le choix d'une base dans un espace
vectoriel de dimension finie  permettait de caractériser
les vecteurs de
permettait de caractériser
les vecteurs de  par les matrices colonnes de leurs composantes
par rapport à cette base. Naturellement, lorsque l'on change de
base, la matrice colonne des composantes change également.
par les matrices colonnes de leurs composantes
par rapport à cette base. Naturellement, lorsque l'on change de
base, la matrice colonne des composantes change également.
Considérons un
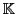 -espace vectoriel de dimension
-espace vectoriel de dimension  , et soient
, et soient
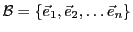 et
et
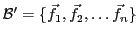 deux bases de
deux bases de  .
Naturellement, les éléments de
.
Naturellement, les éléments de
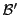 peuvent se décomposer sur la
base
peuvent se décomposer sur la
base
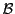 : il existe
: il existe 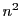 scalaires
scalaires
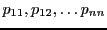 tels que
tels que
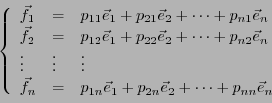 |
(3.3) |

REMARQUE 3.4 Il existe une façon simple d'écrire cette matrice de passage. Partant
du système (
![[*]](crossref.png)
), on peut écrire les matrices
colonne des nouveaux vecteurs de base
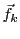
dans la base
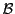
:
Ainsi, la matrice
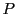
s'obtient en mettant côte
à côte ces matrices colonnes.
EXEMPLE 3.14 Le cas le plus simple est celui où les bases
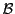
et
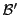
sont identiques:
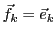
pour tout
.
On vérifie facilement que dans ce cas, la matrice de passage est
la matrice identité.
Si par contre
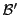 est constituée des mêmes vecteurs que
est constituée des mêmes vecteurs que
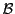 , mais que ceux-ci sont numérotés différemment, la matrice de
passage est toujours constituée uniquement de zéros et de uns, mais
n'est plus la matrice identité. Par exemple, dans
, mais que ceux-ci sont numérotés différemment, la matrice de
passage est toujours constituée uniquement de zéros et de uns, mais
n'est plus la matrice identité. Par exemple, dans
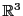 , si
on prend
, si
on prend
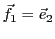 ,
,
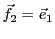 et
et
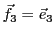 , la
matrice de passage correspondante sera de la forme
, la
matrice de passage correspondante sera de la forme
EXEMPLE 3.15 Dans
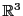
, muni de sa base canonique
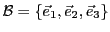
,
on considère les trois vecteurs
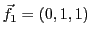
,
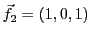
et
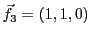
. Ces trois vecteurs
forment une base de
, vérifions le. Supposons qu'il existe
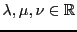
tels que
ceci équivaut au système linéaire homogène
dont on vérifie facilement qu'il n'admet que la solution triviale
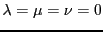
.
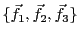
est donc une famille libre
dans
.
Comme
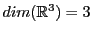
et que cette famille est constituée de 3 vecteurs,
c'est une base de
, que l'on note
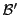
. La matrice de passage
correspondante prend la forme
REMARQUE 3.5 En comparant l'équation (
![[*]](crossref.png)
) à
l'équation (
![[*]](crossref.png)
), on peut voir que
la matrice de passage n'est autre que la matrice de
l'application linéaire identité
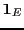
de

par rapport aux bases
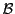
et
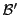
:
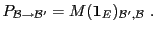 |
(3.4) |
Une conséquence immédiate est
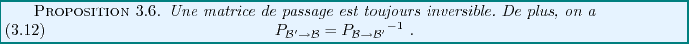
Preuve:
En notant  , on a
, on a
ce qui suffit à montrer cette propriété.
Les matrices de passage fournissent un outil très simple d'utilisation
pour calculer les composantes d'un vecteur dans une nouvelle base
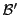 ,
à partir des composantes dans une première base
,
à partir des composantes dans une première base
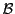 .
.
En effet, considérons deux bases
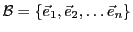 et
et
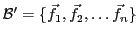 d'un
d'un
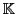 -espace vectoriel
-espace vectoriel  de dimension
de dimension  , et soit
, et soit
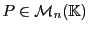 la matrice de passage
correspondante.
la matrice de passage
correspondante.
Soit
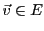 , et soient
, et soient
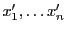 ses composantes par rapport
à la base
ses composantes par rapport
à la base
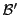 : on écrit
: on écrit
On peut alors écrire aussi
Or,
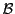 étant une base de
étant une base de  elle aussi, il existe une et une
seule façon de décomposer
elle aussi, il existe une et une
seule façon de décomposer 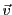 sur
sur
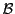 :
:
d'où on déduit, par identification
où on reconnait le produit matriciel
La matrice de passage étant toujours inversible on a donc montré
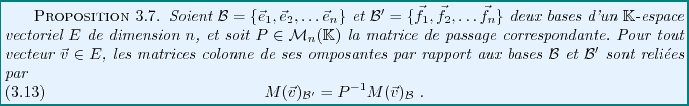
EXEMPLE 3.16 Reprenons l'exemple
![[*]](crossref.png)
. Etant donné un vecteur
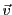
,
de matrice
dans la base
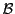
, ses coordonnées dans la base
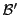
s'obtiennent par
Il faut donc calculer l'inverse de la matrice
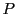
.
Si
alors
ce qui, pour notre choix de
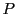
, revient au système linéaire
La solution du système est donnée par
d'où on déduit
et donc les composantes du vecteur
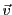
dans la base
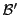
:
Comme on l'a vu, la matrice d'une application linéaire dépend elle aussi
de la base considérée.
Considérons tout d'abord le cas d'un endomorphisme
d'un espace vectoriel  de dimension
de dimension  . Soient, comme plus haut,
. Soient, comme plus haut,
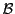 et
et
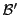 deux bases de
deux bases de  , et soit
, et soit 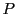 la matrice de
passage correspondante. Soit
la matrice de
passage correspondante. Soit
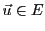 , et soit
, et soit
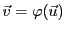 .
On a alors
.
On a alors
où on a noté
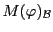 la matrice de
la matrice de  dans la
base
dans la
base
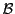 . En restant dans la base
. En restant dans la base
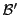 , on a aussi
, on a aussi
Ceci étant vrai pour tout
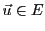 , on a donc montré:
, on a donc montré:
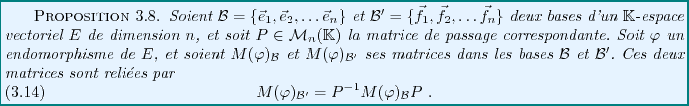
REMARQUE 3.6 Dans le cas plus général d'applications linéaires d'un espace
vectoriel

vers un espace vectoriel

, il est possible de montrer une
propriété similaire, plus complexe, qu'on n'abordera pas ici.
EXEMPLE 3.17 Dans
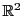
, muni de sa base canonique
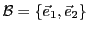
, on considère
les vecteurs
On peut vérifier que la famille
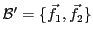
est une base de
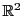
. La
matrice de passage correspondante est la matrice
Comme précédemment, son inverse se calcule directement, et on obtient
Soit
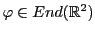
l'endomorphisme de
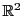
, défini par
La matrice
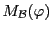
de

dans la base canonique
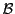
est la matrice
La matrice
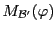
dans la base
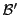
s'obtient quant à elle
grâce au résultat ci-dessus:
On aurait pu obtenir ce résultat différemment, en calculant directement
Ensuite, puisque
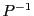
est la matrice de passage
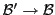
, on
en déduit que
d'où
ce qui conduit au même résultat pour la matrice
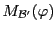
. On peut en fait vérifier que ce second calcul est
tout à fait identique au premier, sous une autre forme.
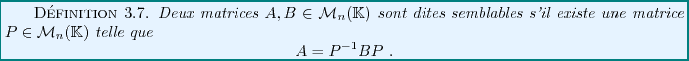
Deux matrices semblables représentent le même endomorphisme
dans deux bases différentes. La matrice 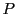 intervenant dans
la définition
intervenant dans
la définition ![[*]](crossref.png) est la matrice de
passage correspondante: ses colonnes représentent les composantes
des nouveaux vecteurs de base dans l'ancienne base.
est la matrice de
passage correspondante: ses colonnes représentent les composantes
des nouveaux vecteurs de base dans l'ancienne base.
On a déjà rencontré auparavant la notion de rang d'une
application linéaire
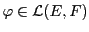 : rappelons qu'il s'agit
de la dimension du sous-espace vectoriel
: rappelons qu'il s'agit
de la dimension du sous-espace vectoriel
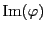 engendré
par les images
engendré
par les images
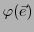 des élements
des élements 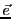 de
de  .
.
Le rang d'une application linéaire peut aussi être compris en
termes matriciels.

EXEMPLE 3.18 Considérons par exemple la matrice
Par définition, le rang de

est donc la dimension du sous-espace vectoriel
de
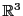
engendré par les vecteurs colonne
Il s'agit d'une famille de 5 vecteurs dans un espace de dimension 3,
elle est donc nécessairement liée. On sait par contre qu'on peut
toujours en extraire une base. Cherchons quelles sont les relations
linéaires entre ces vecteurs, c'est à dire les relations de la forme
pour 5 scalaires
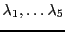
. Ceci équivaut au système
linéaire homogène
En utilisant la méthode du pivot, résoudre ce système
équivaut à échelonner la matrice

elle même
ce qui donne dans un premier temps la matrice
puis, les deux dernières lignes étant équivalentes,
la matrice échelonnée
Ainsi, l'ensemble des solutions de ce système (c'est à dire
l'ensemble des
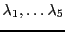
) est un sous-espace vectoriel
de dimension 3 de
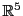
: pour tous
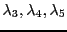
, en
prenant
on a bien
Ceci s'écrit, pour tous
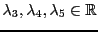
ou encore, pour tous
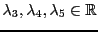
ce qui finalement équivaut aux 3 relations linéaires
Ainsi,
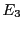
,
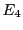
et
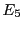
sont complètement déterminés par
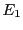
et
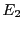
, qui forment une base du sous-espace engendré par
ces 5 vecteurs colonne. Celui-ci est de dimension 2, donc
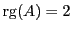
.
Il existe une relation entre le rang d'une application linéaire
et celui de sa matrice.

Notons que ceci implique que le rang d'une matrice est invariant par
changement de bases, puisque le rang de  ne dépend pas
des bases choisies.
ne dépend pas
des bases choisies.
REMARQUE 3.7 Il est possible de montrer que si

est une matrice, et si
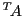
est sa transposée, leurs rangs sont égaux:
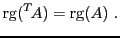 |
(3.5) |
Cette propriété est parfois utile, comme dans l'exemple suivant.
EXEMPLE 3.19 On considère la famille de trois vecteurs de
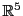
Le rang de la famille
est égal au rang
de la matrice
Cette matrice est la transposée de la matrice

de l'exemple
![[*]](crossref.png)
,
donc
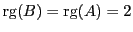
.
Bruno Torresani
2009-02-18

![]() l'application qui à
l'application qui à
![]() associe sa dérivée
(qui est donc une fonction continue)
associe sa dérivée
(qui est donc une fonction continue)
![]() un espace vectoriel,
et soient
un espace vectoriel,
et soient ![]() et
et ![]() deux sous-espaces vectoriels supplémentaires
dans
deux sous-espaces vectoriels supplémentaires
dans ![]() :
:
![]() , on sait donc qu'il existe un unique couple
de réels
, on sait donc qu'il existe un unique couple
de réels
![]() tel que
tel que

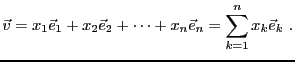
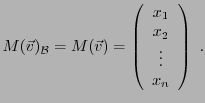
![]() et
et ![]() deux
deux
![]() -espaces vectoriels,
avec
-espaces vectoriels,
avec ![]() et
et ![]() ,
et soit
,
et soit
![]() , on sait que
, on sait que
![]() . Donc,
. Donc,
![]() admet une unique décomposition en combinaison
linéaire de la base
admet une unique décomposition en combinaison
linéaire de la base
![]() de
de ![]() : il existe
une unique famille de scalaires
: il existe
une unique famille de scalaires
![]() telle que
telle que
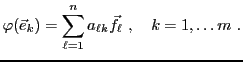

![[*]](crossref.png) ), on peut écrire les matrices
colonne des images
), on peut écrire les matrices
colonne des images
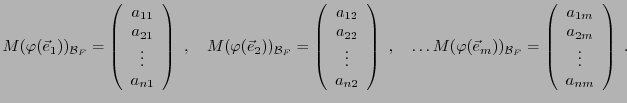
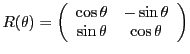
![]() de
de ![]() de l'image d'un vecteur
de l'image d'un vecteur
![]() , connaissant ses composantes par rapport à une base
, connaissant ses composantes par rapport à une base
![]() de
de ![]() .
.

![]() soit de dimension
soit de dimension ![]() , et
que
, et
que ![]() soit de dimension
soit de dimension ![]() .
Soit
.
Soit
![]() . La linéarité de
l'application
. La linéarité de
l'application ![]() donne
donne
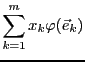
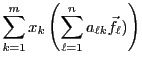
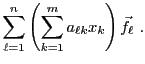
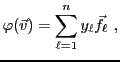
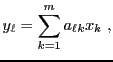
![]() est
une matrice à
est
une matrice à ![]() lignes, la matrice
lignes, la matrice
![]() est une matrice
à
est une matrice
à ![]() lignes, et donc la matrice
lignes, et donc la matrice
![]() est une matrice
à
est une matrice
à ![]() lignes et
lignes et ![]() colonnes. On a bien, conformément aux règles
du calcul matriciel
colonnes. On a bien, conformément aux règles
du calcul matriciel
![[*]](crossref.png) (SUITE)
Reprenons l'exemple de la rotation ci-dessus. Soit
(SUITE)
Reprenons l'exemple de la rotation ci-dessus. Soit
![]() , et soit
, et soit
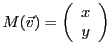
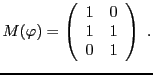
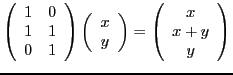
![[*]](crossref.png) ci dessous)
en fonction de leurs matrices
ci dessous)
en fonction de leurs matrices
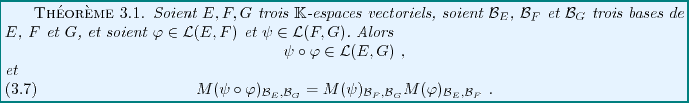
![]() , et soit
, et soit
![]() sa matrice colonne. Par
l'associativité du produit matriciel, on a
sa matrice colonne. Par
l'associativité du produit matriciel, on a
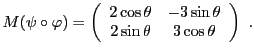
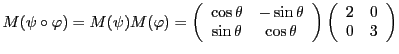
![]() soit bijective.
Alors il existe
soit bijective.
Alors il existe
![]() telle que
telle que
![]() .
Dans ce cas, on peut associer à
.
Dans ce cas, on peut associer à
![]() une matrice, qui
est reliée à
une matrice, qui
est reliée à
![]() . Plus précisément, on a:
. Plus précisément, on a:

![]() soit bijective. Alors on sait que
soit bijective. Alors on sait que
![]()
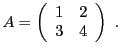
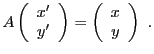
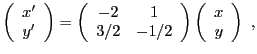
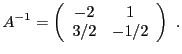

![]() .
.
![]() . Alors
il existe
. Alors
il existe
![]() et
et
![]() tels que
tels que
![]() , et
, et
![]() . Donc,
. Donc,
![]() . On a
. On a

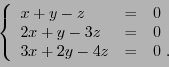
![]()
![]() ; alors
; alors
![]() et
et
![]() . Donc
. Donc
![]()
![]() soit injective. Alors, comme
soit injective. Alors, comme
![]() ,
,
![]() implique nécessairement
que
implique nécessairement
que
![]() . Réciproquement, supposons que
. Réciproquement, supposons que
![]() ,
et soient
,
et soient
![]() tels que
tels que
![]() .
Alors par linéarité de
.
Alors par linéarité de ![]() , on a
, on a
![]() , d'où
, d'où
![]() , et donc
, et donc
![]() .
.
![]()

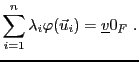
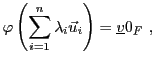
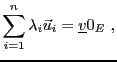
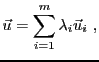
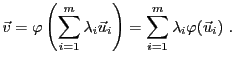
![\begin{theorem}[Th\'eor\\lq eme du rang (ou de la dimension)]
Soient $E$\ et $F$\ d...
...(E) = {\rm rg}(\varphi) + dim({\rm Ker}(\varphi))
\end{displaymath}\end{theorem}](img794.png)
![]() . Il existe
. Il existe
![]() tel que
tel que
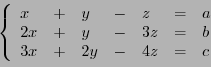
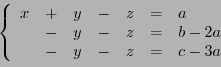

![]() soit
injective. Alors
soit
injective. Alors
![]() , est donc de dimension nulle.
Par conséquent,
, est donc de dimension nulle.
Par conséquent,
![]() soit surjective. Alors
soit surjective. Alors
![]() , d'où on déduit, par les mêmes
arguments, que
, d'où on déduit, par les mêmes
arguments, que
![]() , d'où
, d'où ![]() est
nécessairement injective.
est
nécessairement injective.
![]()

![[*]](crossref.png) ), on peut écrire les matrices
colonne des nouveaux vecteurs de base
), on peut écrire les matrices
colonne des nouveaux vecteurs de base
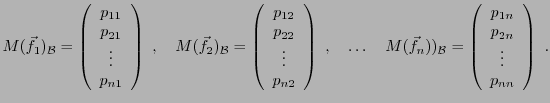
![]() est constituée des mêmes vecteurs que
est constituée des mêmes vecteurs que
![]() , mais que ceux-ci sont numérotés différemment, la matrice de
passage est toujours constituée uniquement de zéros et de uns, mais
n'est plus la matrice identité. Par exemple, dans
, mais que ceux-ci sont numérotés différemment, la matrice de
passage est toujours constituée uniquement de zéros et de uns, mais
n'est plus la matrice identité. Par exemple, dans
![]() , si
on prend
, si
on prend
![]() ,
,
![]() et
et
![]() , la
matrice de passage correspondante sera de la forme
, la
matrice de passage correspondante sera de la forme


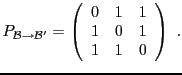
![[*]](crossref.png) ) à
l'équation (
) à
l'équation (![[*]](crossref.png) ), on peut voir que
la matrice de passage n'est autre que la matrice de
l'application linéaire identité
), on peut voir que
la matrice de passage n'est autre que la matrice de
l'application linéaire identité ![]()
![]() , on a
, on a
![]() et
et
![]() d'un
d'un
![]() -espace vectoriel
-espace vectoriel ![]() de dimension
de dimension ![]() , et soit
, et soit
![]() la matrice de passage
correspondante.
la matrice de passage
correspondante.
![]() , et soient
, et soient
![]() ses composantes par rapport
à la base
ses composantes par rapport
à la base
![]() : on écrit
: on écrit
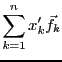
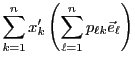
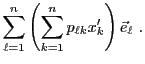
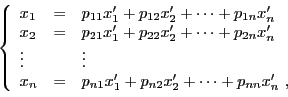

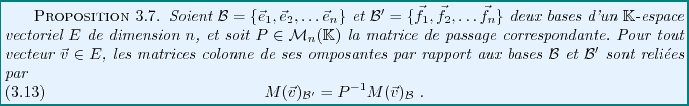
![[*]](crossref.png) . Etant donné un vecteur
. Etant donné un vecteur 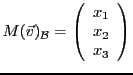
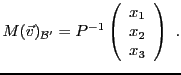
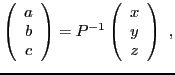
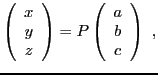
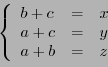
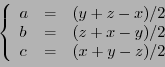
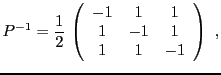
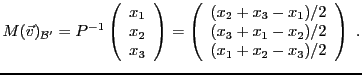
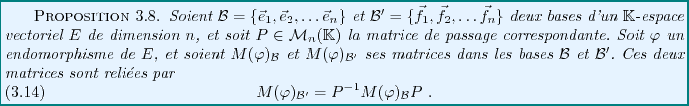
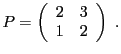
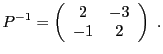
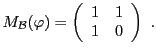
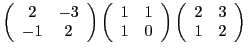
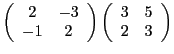
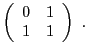
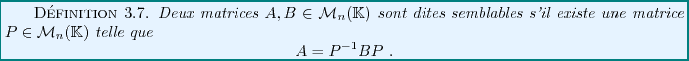
![]() intervenant dans
la définition
intervenant dans
la définition ![[*]](crossref.png) est la matrice de
passage correspondante: ses colonnes représentent les composantes
des nouveaux vecteurs de base dans l'ancienne base.
est la matrice de
passage correspondante: ses colonnes représentent les composantes
des nouveaux vecteurs de base dans l'ancienne base.

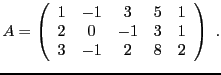
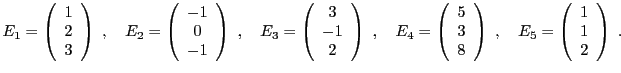
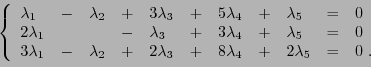
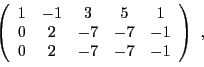
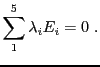
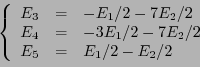


![[*]](crossref.png) ,
donc
,
donc