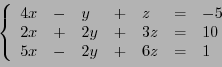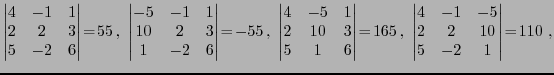Subsections
Déterminants, inversion de matrices
On a déjà vu dans le chapitre précédent comment
on peut dans des cas simples calculer l'inverse d'une matrice.
Dans des cas plus complexes, comme par exemple dans le cas de matrices de
grandes taille, il est parfois utile d'utiliser une approche différente,
basée sur la notion de déterminant.
Soient
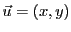 et
et
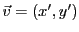 deux vecteurs de
deux vecteurs de
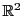 . On se pose le problème de calculer l'aire
. On se pose le problème de calculer l'aire
 du
parallélogramme engendré par
du
parallélogramme engendré par 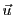 et
et 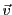 .
.
Une construction géométrique simple (voir
FIG. ![[*]](crossref.png) ) permet de montrer que
cette aire vaut
) permet de montrer que
cette aire vaut
Cette quantité est directement reliée à ce que l'on
appelle le déterminant
des vecteurs 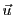 et
et 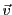 .
.
Figure:
Détermination géométrique de l'aire d'un parallèlogramme,
et relation avec le déterminant des deux vecteurs engendrant ce
parallélogramme.
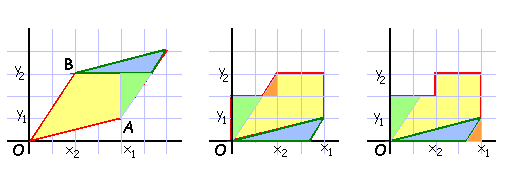 |
REMARQUE 4.1 Cette construction géométrique a aussi la vertu de montrer que
contrairement à ce que la formule ci-dessus pourrait laisser croire,
le déterminant est indépendant du repère orthonormé choisi.
Le déterminant est quant à lui défini de la façon suivante:
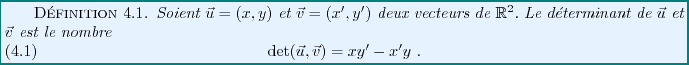
Ce déterminant possède certaines propriétés simples, dont on verra
la forme plus générale dans le cas de matrices plus grandes. Les
propriétés les plus importantes sont les propriétés de
bilinéarité et d'antisymétrie.
Le déterminant d'une matrice 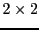 est défini de façon similaire,
en utilisant les colonnes des matrices
est défini de façon similaire,
en utilisant les colonnes des matrices
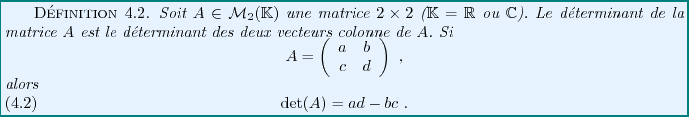
On note également le déterminant d'une matrice sous la forme
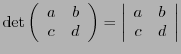 |
(4.6) |
EXEMPLE 4.1 On voit facilement que
EXEMPLE 4.2 matrice de rotation. Nous avons déjà rencontré les matrices
de rotation d'angle
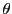
du plan
Un calcul simple montre que
ce qui est somme toute logique si on se souvient que le déterminant
de la matrice est égal au déterminant de ses colonnes, qui est égal
(au signe près) à l'aire du parallèlogramme qu'ils définissent,
à savoir un carré de côté 1.
On peut vérifier directement la propriété suivante à partir de
la définition du déterminant.
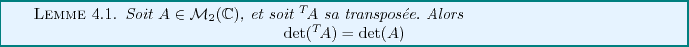
Le déterminant des matrices 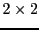 hérite des propriétés
du déterminant des vecteurs, à savoir les propriétés d'antisymétrie
et de bilinéarité. Ces propriétés, combinées au lemme ci-dessus,
conduisent aux propriétés suivantes.
hérite des propriétés
du déterminant des vecteurs, à savoir les propriétés d'antisymétrie
et de bilinéarité. Ces propriétés, combinées au lemme ci-dessus,
conduisent aux propriétés suivantes.
- Le déterminant d'une matrice
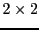 change de signe
lorsque l'on permute les deux colonnes de la matrice.
change de signe
lorsque l'on permute les deux colonnes de la matrice.
- En appliquant cette propriété à la transposée
de la matrice
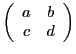 on montre aussi que le déterminant d'une matrice
on montre aussi que le déterminant d'une matrice 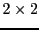 change de signe
lorsque l'on permute les deux lignes de la matrice:
change de signe
lorsque l'on permute les deux lignes de la matrice:
- Bilinéarité: pour tous
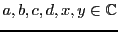 ,
,
et
- En appliquant cette propriété à la transposée de la matrice
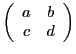 , on a aussi
pour tous
, on a aussi
pour tous
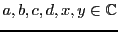 ,
,
et
Considérons le système linéaire de deux équations à deux
inconnues
Supposons par exemple 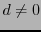 ; en éliminant
; en éliminant 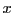 de la seconde équation,
on obtient
de la seconde équation,
on obtient
d'où en reportant dans la première équation,
on tire, à condition que
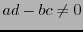 ,
,
et de là
En termes matriciels, le système peut aussi s'écrire
et on reconnaît
Ceci étant vrai pour tous 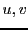 , on en déduit
, on en déduit
On voit bien apparaître le rôle du déterminant
dans ce résultat. Comme on le verra, ce résultat restera vrai
pour des matrices carrées de taille quelconque.
Notons aussi que la solution est de la forme
Comme on l'a vu, le dénominateur de 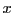 et
et 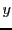 n'est autre que le
déterminant de la matrice
n'est autre que le
déterminant de la matrice
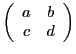 .
Le numérateur de
.
Le numérateur de 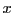 est le déterminant d'une autre matrice, obtenue à
partir de
est le déterminant d'une autre matrice, obtenue à
partir de
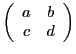 en
substituant à la première colonne la colonne
en
substituant à la première colonne la colonne
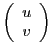 . Le numérateur
de
. Le numérateur
de  est quant à lui le déterminant de la matrice obtenue à
partir de
est quant à lui le déterminant de la matrice obtenue à
partir de
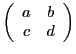 en
substituant à la seconde colonne la colonne
en
substituant à la seconde colonne la colonne
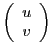 .
.
Là encore, ce résultat n'est pas une coïncidence, mais n'est que
le cas particulier d'une situation plus générale, dans laquelle on
verra que les déterminants jouent un rôle central pour la
résolution de systèmes linéaires.
Comme en dimension 2, il est possible d'introduire le déterminant de trois
vecteurs de
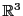 de façon géométrique: le volume du
parallélépipède engendré par ces trois vecteurs est
égal à la valeur absolue du déterminant de ces trois vecteurs.
On définit alors le déterminant d'une matrice
de façon géométrique: le volume du
parallélépipède engendré par ces trois vecteurs est
égal à la valeur absolue du déterminant de ces trois vecteurs.
On définit alors le déterminant d'une matrice  comme le
déterminant de ses trois vecteurs colonne.
comme le
déterminant de ses trois vecteurs colonne.
Cette définition est toutefois difficile à utiliser en dimensions
supérieures, et on préfère en donner une autre, plus opératoire.
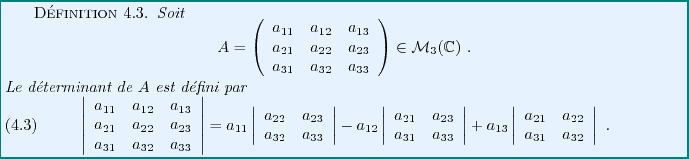
On peut vérifier que ce déterminant possède toutes les propriétés
que nous avions déjà rencontrées dans le cas des matrices 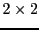 :
:
- Trilinéarité: pour toute matrice
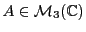 , et pour
tous
, et pour
tous
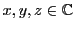 ,
,
Aussi, pour tout
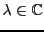 ,
,
et de même pour les colonnes 2 et 3.
- Antisymétrie: lorsque l'on permute deux colonnes adjacentes,
le déterminant change de signe: par exemple
Par contre, ceci n'est plus nécessairement vrai lorsque les
colonnes ne sont pas adjacentes. Par exemple, on a en permutant cette fois
les colonnes 2 et 3 de cette dernière matrice
les deux changements de signes provenant des deux permutations s'étant compensés.
Calculons maintenant, pour
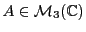 ,
,
Ainsi, le Lemme ![[*]](crossref.png) reste vrai pour les matrices
reste vrai pour les matrices 
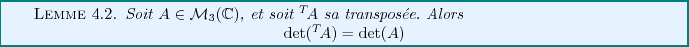
Par conséquent, on peut appliquer toutes les propriétés que nous avons
énoncées ci-dessus (bilinéarité, antisymétrie,...) en remplaçant
les colonnes par les lignes.
De plus, ces propriétés donnent d'autres possibilités pour calculer le
déterminant d'une matrice. On a besoin pour cela d'introduire une notation
nouvelle. Etant donnée
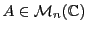 , on notera
, on notera
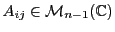 la matrice à
la matrice à 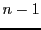 lignes et
lignes et 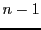 colonnes obtenue en supprimant la
colonnes obtenue en supprimant la 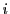 -ième ligne et
la
-ième ligne et
la 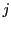 -ième colonne de
-ième colonne de  :
:
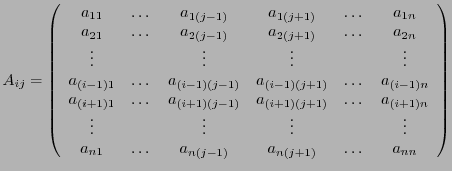 |
(4.7) |

On a alors

Ce théorème est intéressant, car il montre qu'il existe plusieurs façons
différentes de calculer un déterminant, et qu'il est donc possible de
choisir celle qui sera la plus simple, comme on va le voir dans l'exemple
ci-dessous.
EXEMPLE 4.3 Soit à calculer
En développant ce déterminant par rapport à sa première ligne, comme
dans la définition, on a à calculer trois déterminants
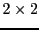
.
Si par
contre on développe par rapport à la deuxième ligne, on obtient
Le résultat suivant est essentiel, dans la mesure où il permet
dans certains cas de montrer qu'un déterminant est nul sans faire
le moindre calcul.

Preuve:
Il suffit de montrer cette proposition dans le cas des colonnes.
Pour démontrer le cas des lignes, il suffit d'appliquer les résultats
concernant les colonnes à la transposée de la matrice  , qui possède le
même déterminant.
, qui possède le
même déterminant.
- On voit facilement que si la première colonne de
 est nulle, le déterminant de
est nulle, le déterminant de  est nul. Si
est nul. Si  possède une colonne nulle,
on peut par permutations se ramener à une matrice dont la première colonne
est nulle. Le déterminant de cette dernière matrice (qui est égal au
déterminant de
possède une colonne nulle,
on peut par permutations se ramener à une matrice dont la première colonne
est nulle. Le déterminant de cette dernière matrice (qui est égal au
déterminant de  , à un signe près) est nul, et donc
, à un signe près) est nul, et donc
 .
.
- Supposons que
 possède deux colonnes adjacentes identiques; alors en les
permutant (ce qui ne change rien !), on change le signe du déterminant. Ce
dernier est nécessairement nul. Si
possède deux colonnes adjacentes identiques; alors en les
permutant (ce qui ne change rien !), on change le signe du déterminant. Ce
dernier est nécessairement nul. Si  possède deux colonnes identiques,
on peut par permutations remplacer
possède deux colonnes identiques,
on peut par permutations remplacer  par une matrice
par une matrice  ayant (au signe
près) le même déterminant et deux colonnes adjacentes identiques. Donc
ayant (au signe
près) le même déterminant et deux colonnes adjacentes identiques. Donc
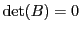 , d'où
, d'où
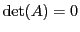 .
.
- Supposons que
 possède deux colonnes proportionnelles, par exemple
possède deux colonnes proportionnelles, par exemple
Alors
- Finalement, supposons par exemple que la seconde colonne soit combinaison
linéaire de la première et la troisième:
Alors d'après les propriétés de linéarité, on a
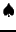
Il est possible de démontrer que la dernière propriété est en
fait une condition nécessaire et suffisante:
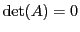 si et seulement si
il existe une colonne de
si et seulement si
il existe une colonne de  qui soit combinaison linéaire des autres, c'est
à dire si la famille des colonnes n'est pas libre.
Ce résultat a un corollaire immédiat:
qui soit combinaison linéaire des autres, c'est
à dire si la famille des colonnes n'est pas libre.
Ce résultat a un corollaire immédiat:
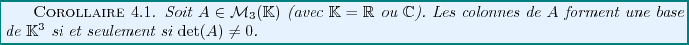
Finalement, en se basant sur les propriétés ci-dessus, on peut
facilement voir que la méthode du pivot de Gauss peut
s'appliquer pour calculer un déterminant.

EXEMPLE 4.4 En appliquant cette règle, on voit par exemple que
Dans ce calcul on a utilisé le pivot, puis le fait que le déterminant
d'une matrice triangulaire supérieure est égal au produit de ses
termes diagonaux.
On peut également organiser le calcul différemment, comme suit:
On a ici utilisé le pivot différemment, puis le fait que le déterminant
d'une matrice triangulaire inférieure est égal au produit de ses
termes diagonaux.
La définition du déterminant d'une matrice carrée
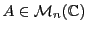 se
fait par récurrence.
se
fait par récurrence.
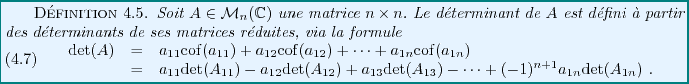
EXEMPLE 4.5 Considérons la matrice
L'application directe de la définition donne
EXEMPLE 4.6 Les exemples les plus simples sont ceux de la matrice nulle
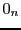
et de la matrice identité
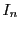
. On a dans ces cas
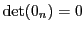
, et
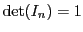
.
EXEMPLE 4.7 Il est facile aussi de montrer, à partir de cette définition, que le
déterminant d'une matrice diagonale est égal au produit des termes
diagonaux:
Ceci reste vrai lorsque la matrice est triangulaire supérieure
(c'est à dire lorsque tous les éléments situés en
dessous de la diagonale sont nuls), ou triangulaire
inférieure (c'est à dire lorsque tous les éléments situés
au dessus de la diagonale sont nuls).
Les propriétés essentielles des déterminants sont
résumées dans le théorème fondamental suivant.

Comme dans le cas des matrices 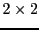 et
et 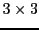 , on a les résultats
fondamentaux
, on a les résultats
fondamentaux
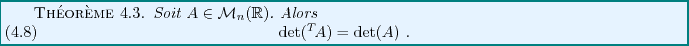
Le résultat suivant est le pendant direct de la
proposition ![[*]](crossref.png) ,
qui se généralise donc à la dimension
,
qui se généralise donc à la dimension  . On peut vérifier que la
preuve de la proposition
. On peut vérifier que la
preuve de la proposition ![[*]](crossref.png) n'a rien de spécifique aux
matrices
n'a rien de spécifique aux
matrices 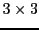 , et reste valable dans un cas quelconque.
, et reste valable dans un cas quelconque.

Il s'ensuit que l'on ne modifie pas le déterminant d'une matrice lorsque
- on ajoute à une ligne une combinaison linéaire quelconque
des autres lignes.
- on ajoute à une colonne une combinaison linéaire quelconque
des autres colonnes.
Ceci permet d'utiliser des techniques que nous avons déjà vu
en étudiant la méthode du pivot pour calculer des déterminants:
on peut jouer sur les lignes (ou les colonnes) pour remplacer des coefficients
par des valeurs nulles, et ainsi simplifier des calculs de déterminants.
EXEMPLE 4.9 Soit à calculer le déterminant
En soustrayant des lignes, on a
Il suffit alors de développer par rapport à la première colonne,
pour obtenir
On s'est ainsi épargné des calculs pénibles.
Comme en dimensions 2 et 3, ce résultat a un corollaire immédiat

Le résultat suivant est une généralisation directe du
Théorème ![[*]](crossref.png)

EXEMPLE 4.10 Reprenons l'exemple
![[*]](crossref.png)
, et considérons la matrice
En développant le déterminant suivant la première colonne, on obtient
EXEMPLE 4.11 En utilisant cette propriété, on peut montrer que le déterminant
d'une matrice triangulaire inférieure est égal au produit des termes
diagonaux:
il suffit pour cela de développer suivant la première ligne;
seul le premier terme est non nul, et conduit au déterminant
d'une matrice
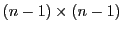
, elle aussi triangulaire inférieure,
à laquelle on peut appliquer le même traitement, et ainsi de suite.
De même, en développant suivant la première colonne, on peut
montrer que le déterminant d'une matrice triangulaire supérieure
est égal au produit des termes diagonaux:
Les déterminants ont un comportement très simple vis à vis du produit
matriciel, comme le montre le résultat suivant, donné sans démonstration.
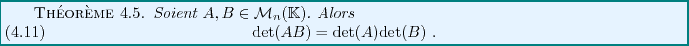
Ce résultat a un certain nombre d'importants corollaires.
Supposons que  soit inversible.
Alors, de
soit inversible.
Alors, de
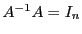 , on déduit que
, on déduit que
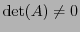 , et que
, et que
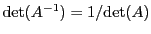 . Inversement, supposons que
. Inversement, supposons que
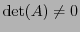 . Alors les
colonnes de
. Alors les
colonnes de  forment une base de
forment une base de
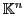 , et
, et  n'est autre que la matrice
de passage de la base canonique à cette nouvelle base. Une matrice de passage
étant toujours inversible, on en déduit que
n'est autre que la matrice
de passage de la base canonique à cette nouvelle base. Une matrice de passage
étant toujours inversible, on en déduit que  est inversible.
On a donc montré:
est inversible.
On a donc montré:
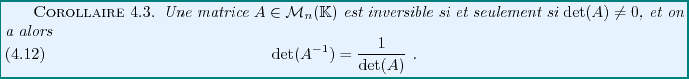
Soient  et
et  deux matrices semblables
, c'est à dire
représentant le même endomorphisme dans deux bases différentes.
Alors on sait que
deux matrices semblables
, c'est à dire
représentant le même endomorphisme dans deux bases différentes.
Alors on sait que
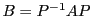 ,
, 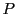 étant la matrice de passage.
Par suite, on a
étant la matrice de passage.
Par suite, on a
d'où
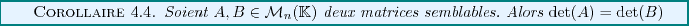
Soit  un
un
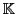 -espace vectoriel, et soit
-espace vectoriel, et soit
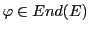 . On peut
définir la notion de déterminant de
. On peut
définir la notion de déterminant de  .
.
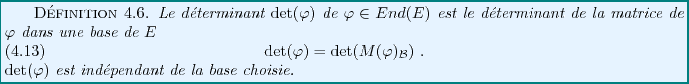
Nous pouvons facilement vérifier ce dernier point. Soit
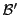 une autre base de
une autre base de  , et soit
, et soit
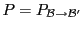 la matrice de passage
correspondante. On a alors
la matrice de passage
correspondante. On a alors
d'où
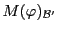 et
et
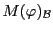 sont semblables, et
ont donc même déterminant.
sont semblables, et
ont donc même déterminant.
Le résultat suivant permet de calculer effectivement l'inverse d'une matrice,
tout du moins lorsque celle-ci n'est pas trop grande.

EXEMPLE 4.12 On considère la matrice
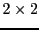
et on suppose que son déterminant
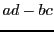
est non nul. La matrice des
cofacteurs de
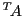
est la matrice
d'où
EXEMPLE 4.13 Soit
On a
et donc, comme
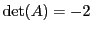
EXEMPLE 4.14 Considérons maintenant la matrice
Le calcul donne
et donc, puisque
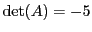
,
Une des applications de ce que nous venons de voir concerne
l'utilisation des déterminants pour la résolution de
systèmes linéaires.
On considère des systèmes linéaires de la forme
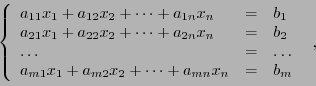 |
(4.8) |
que l'on met sous forme matricielle
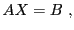 |
(4.9) |
où
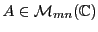 , et où
, et où 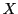 et
et  sont des matrices colonne à
sont des matrices colonne à
 et
et 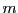 lignes respectivement.
lignes respectivement.

Les systèmes de Cramer peuvent être résolus de façon simple,
grâce à ce que nous avons vu plus haut. Comme
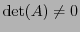 ,
,
 est inversible, et on peut donc écrire
est inversible, et on peut donc écrire
En explicitant 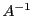 et son action sur
et son action sur  , on peut alors montrer
le résultat suivant, donné ici sans démonstration.
, on peut alors montrer
le résultat suivant, donné ici sans démonstration.

EXEMPLE 4.15 Considérons le système
On voit facilement par le calcul que
d'où on déduit directement la solution
REMARQUE 4.2 Lorsque le déterminant de la matrice

est nul, la méthode de Cramer
ne s'applique plus. Le système est soit inconsistent (c'est à dire
qu'il n'existe pas de solution), soit dépendant (il existe une infinité
de solutions). Dans un cas comme dans l'autre, une autre méthode
doit être employée.
REMARQUE 4.3 Pour conclure, remarquons que le calcul d'un déterminant peut
faire intervenir un très grand nombre de termes lorsque la matrice
est de grande taille. Ainsi, utiliser des déterminants pour
résoudre des systèmes linéaires de grande taille n'est pas
nécessairement à conseiller. Il est dans ce cas préférable
de revenir à la méthode du pivot.
Bruno Torresani
2009-02-18
![[*]](crossref.png) ) permet de montrer que
cette aire vaut
) permet de montrer que
cette aire vaut
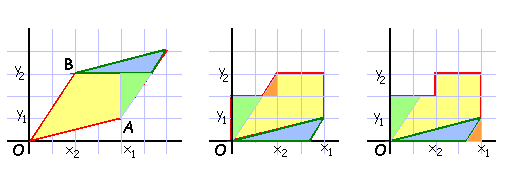
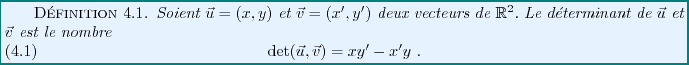
![]() est défini de façon similaire,
en utilisant les colonnes des matrices
est défini de façon similaire,
en utilisant les colonnes des matrices
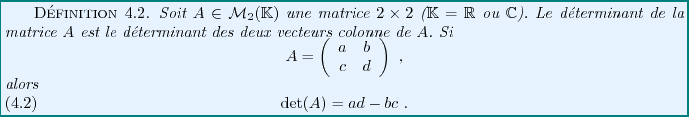
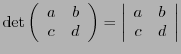
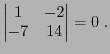
![]()
![]() hérite des propriétés
du déterminant des vecteurs, à savoir les propriétés d'antisymétrie
et de bilinéarité. Ces propriétés, combinées au lemme ci-dessus,
conduisent aux propriétés suivantes.
hérite des propriétés
du déterminant des vecteurs, à savoir les propriétés d'antisymétrie
et de bilinéarité. Ces propriétés, combinées au lemme ci-dessus,
conduisent aux propriétés suivantes.
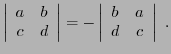
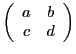 on montre aussi que le déterminant d'une matrice
on montre aussi que le déterminant d'une matrice 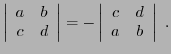
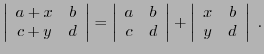
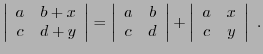
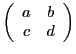 , on a aussi
pour tous
, on a aussi
pour tous
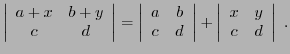
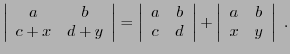
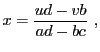
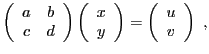
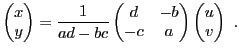
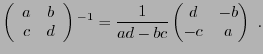
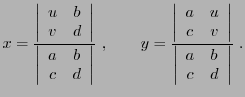
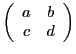 .
Le numérateur de
.
Le numérateur de 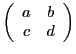 en
substituant à la première colonne la colonne
en
substituant à la première colonne la colonne
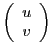 . Le numérateur
de
. Le numérateur
de 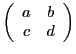 en
substituant à la seconde colonne la colonne
en
substituant à la seconde colonne la colonne
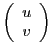 .
.
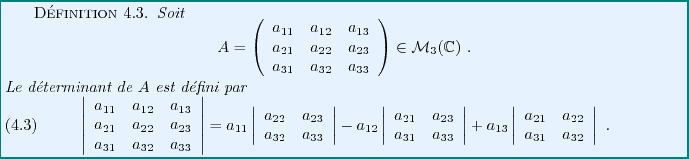
![]() :
:
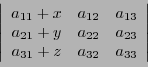
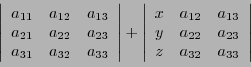
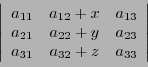
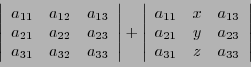

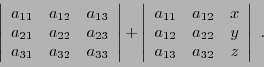
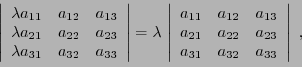
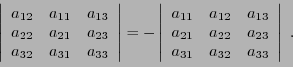
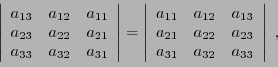
![]() ,
,
![[*]](crossref.png) reste vrai pour les matrices
reste vrai pour les matrices ![]() , on notera
, on notera
![]() la matrice à
la matrice à ![]() lignes et
lignes et ![]() colonnes obtenue en supprimant la
colonnes obtenue en supprimant la ![]() -ième ligne et
la
-ième ligne et
la ![]() -ième colonne de
-ième colonne de ![]() :
:
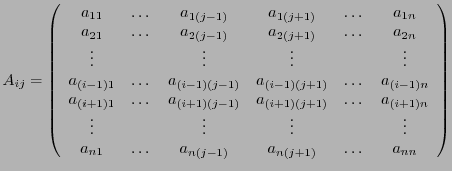
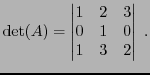
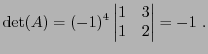

![]() , qui possède le
même déterminant.
, qui possède le
même déterminant.
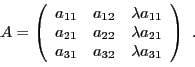

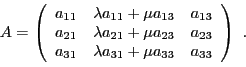
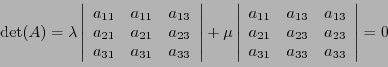
![]() si et seulement si
il existe une colonne de
si et seulement si
il existe une colonne de ![]() qui soit combinaison linéaire des autres, c'est
à dire si la famille des colonnes n'est pas libre.
Ce résultat a un corollaire immédiat:
qui soit combinaison linéaire des autres, c'est
à dire si la famille des colonnes n'est pas libre.
Ce résultat a un corollaire immédiat:
![]()

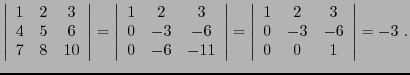
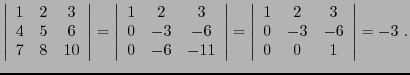
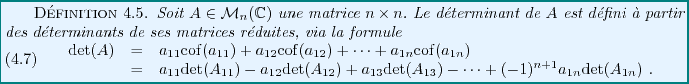
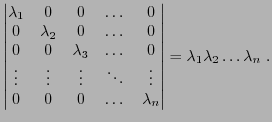



![]() et
et ![]() , on a les résultats
fondamentaux
, on a les résultats
fondamentaux
![]()
![[*]](crossref.png) ,
qui se généralise donc à la dimension
,
qui se généralise donc à la dimension ![]() . On peut vérifier que la
preuve de la proposition
. On peut vérifier que la
preuve de la proposition ![[*]](crossref.png) n'a rien de spécifique aux
matrices
n'a rien de spécifique aux
matrices ![]() , et reste valable dans un cas quelconque.
, et reste valable dans un cas quelconque.



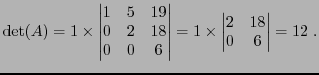
![]()
![[*]](crossref.png)

![[*]](crossref.png) , et considérons la matrice
, et considérons la matrice
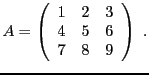
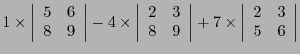
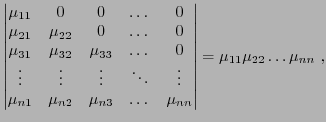

![]() soit inversible.
Alors, de
soit inversible.
Alors, de
![]() , on déduit que
, on déduit que
![]() , et que
, et que
![]() . Inversement, supposons que
. Inversement, supposons que
![]() . Alors les
colonnes de
. Alors les
colonnes de ![]() forment une base de
forment une base de
![]() , et
, et ![]() n'est autre que la matrice
de passage de la base canonique à cette nouvelle base. Une matrice de passage
étant toujours inversible, on en déduit que
n'est autre que la matrice
de passage de la base canonique à cette nouvelle base. Une matrice de passage
étant toujours inversible, on en déduit que ![]() est inversible.
On a donc montré:
est inversible.
On a donc montré:
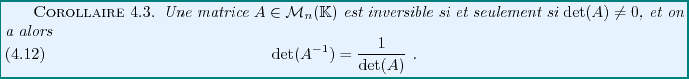
![]() et
et ![]() deux matrices semblables
, c'est à dire
représentant le même endomorphisme dans deux bases différentes.
Alors on sait que
deux matrices semblables
, c'est à dire
représentant le même endomorphisme dans deux bases différentes.
Alors on sait que
![]() ,
, ![]() étant la matrice de passage.
Par suite, on a
étant la matrice de passage.
Par suite, on a
![]() un
un
![]() -espace vectoriel, et soit
-espace vectoriel, et soit
![]() . On peut
définir la notion de déterminant de
. On peut
définir la notion de déterminant de ![]() .
.
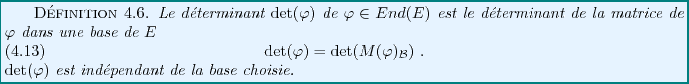
![]() une autre base de
une autre base de ![]() , et soit
, et soit
![]() la matrice de passage
correspondante. On a alors
la matrice de passage
correspondante. On a alors

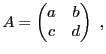
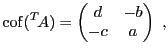
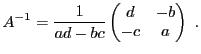
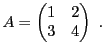
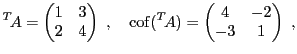
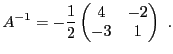
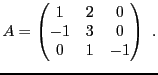
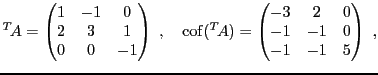
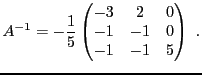
![]() ,
,
![]() est inversible, et on peut donc écrire
est inversible, et on peut donc écrire
![]() et son action sur
et son action sur ![]() , on peut alors montrer
le résultat suivant, donné ici sans démonstration.
, on peut alors montrer
le résultat suivant, donné ici sans démonstration.