Next: Résolution d'équations différentielles par Up: Equations différentielles Previous: La méthode de Frobenius
Pour espérer existence et unicité de solutions de cette équation
ou d'équations associées (voir ci-dessous), on doit la complèter
par deux conditions supplémentaires, des
conditions aux bords. On choisit
généralement des conditions aux bords de la forme
![]() , ou plus généralement des conditions
qui assurent que
, ou plus généralement des conditions
qui assurent que
![]() en
en ![]() et
et ![]() .
.
Ceci définit un opérateur différentiel ![]() , dont l'adjoint est défini par
, dont l'adjoint est défini par
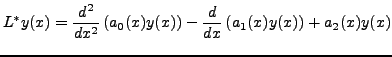 |
(2.24) |
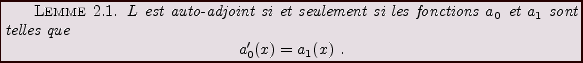
![$\displaystyle J[y] = \frac1{2}\int_a^b [p(x) y'(x)^2 + q(x) y(x)^2]\,dx
$](img536.png)
avec conditions aux bords
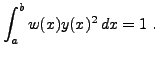
![[*]](crossref.png) )
peut toujours se mettre sous la forme (
)
peut toujours se mettre sous la forme (![[*]](crossref.png) ),
en la multipliant terme à terme par le facteur intégrant
),
en la multipliant terme à terme par le facteur intégrant
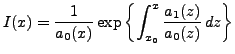
et en posant
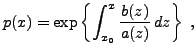
et
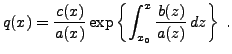

dont on a déjà vu qu'elle peut se résoudre via l'équation caractéristique
Les solutions sont de la forme
En imposant les conditions aux bords
on aboutit à
et les fonctions propres correspondantes sont
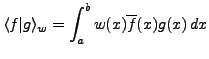
définissant l'espace
![$\displaystyle L^2([a,b],w) = \left\{f: [a,b]\to\mathbb{C}\, ,\ \int_a^b w(x)
\vert f(x)\vert^2\,dx <\infty\right\}\ ,
$](img557.png)
dont on peut montrer qu'il s'agit d'un espace de Hilbert.
Pour cela, soient ![]() et
et ![]() deux valeurs propres, et
deux valeurs propres, et
![]() et
et ![]() les fonctions propres associées. On a alors
les fonctions propres associées. On a alors
![$\displaystyle \left[\frac {d}{dx}p(x)\frac{d}{dx}\right]y_m(x)$](img562.png) |
|||
![$\displaystyle \left[\frac {d}{dx}p(x)\frac{d}{dx}\right]y_n(x)$](img564.png) |
![$\displaystyle \int_a^b \left( \overline{y_m}(x)\left[p(x)y_n'(x)\right]' -
y_n(...
...= (\lambda_n -\overline{\lambda_m}) \int_a^b w(x) \overline{y_m}(x) y_n(x)\,dx
$](img568.png)
Après intégration par parties, en utilisant les conditions aux bords pour éliminer les termes tout intégrés, on obtient
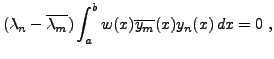
d'où on déduit:
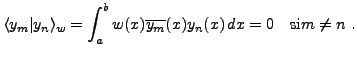
Il est possible de montrer de plus que les fonctions propres
sont complètes dans
![]() : une fonction
: une fonction
![]() telle que
telle que
![]() est nécessairement nulle:
est nécessairement nulle: ![]() . Par conséquent, on a
. Par conséquent, on a

Notons que ceci implique directement que
![]() ,
,
| (2.27) |
Bruno Torresani 2007-06-26