Next: Equations aux dérivées partielles Up: Equations différentielles Previous: Problème de Sturm-Liouville
où on a défini la transformée de Fourier par
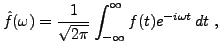 |
(2.28) |
où
En faisant l'hypothèse que
d'où on déduit la solution (dans l'espace de Fourier
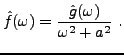
Une transformation de Fourier inverse (utilisant le théorème des résidus, ou une table de transformées de Fourier) conduit alors à la solution
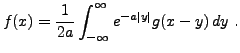
(où
Ensuite, si la fonction
A l'instar de la transformation de Fourier, la transformation de Laplace a la propriété marquante de transformer une équation différentielle à coefficients constants en équation algébrique.
| (2.30) |
![[*]](crossref.png) ) (il est
possible de démontrer dans un cadre plus général l'existence de
solutions satisfaisant à de telles conditions), et que
) (il est
possible de démontrer dans un cadre plus général l'existence de
solutions satisfaisant à de telles conditions), et que
où
soit encore, pour
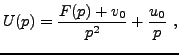
dans un domaine de valeurs de
On peut toutefois utiliser ce que l'on sait déjà, c'est à dire les propriétés de linéarité de la transformation de Laplace, sa relation avec le produit de convolution ainsi que les quelques transformées de Laplace déjà vues.
Ainsi, on sait que l'original de Laplace de la fonction ![]() est
la fonction de Heaviside
est
la fonction de Heaviside ![]() , et que l'original de Laplace de
, et que l'original de Laplace de
![]() est la fonction
est la fonction
![]() . Par ailleurs,
l'original de Laplace de la fonction
. Par ailleurs,
l'original de Laplace de la fonction
![]() est le produit de
convolution de
est le produit de
convolution de ![]() par la fonction
par la fonction
![]() . On en déduit donc
. On en déduit donc
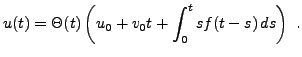
Bruno Torresani 2007-06-26