Subsections
Classiquement, le calcul des variations s'applique pour rechercher
des minima ou maxima d'une fonction. Il consiste à partir d'une solution
donnée, et examiner les solutions proches pour voir si elles sont meilleures
ou moins bonnes. Ceci se fait à l'aide de la dérivation.
Il est utile de rappeler dans un premier temps les bases du calcul
différentiel sur les fonctions de plusieurs variables.
Soit
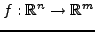 , et soit
, et soit
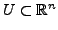 .
Soit
.
Soit
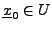 .
.

Le premier résultat essentiel est la proposition suivante
![\begin{proposition}[Taylor]
Soit $f:{\mathbb{R}}^n\to{\mathbb{R}}^m$, de classe ...
...erline{h}}\to 0}\epsilon({\underline{h}}) = 0\ .
\end{equation}\end{proposition}](img16.png)
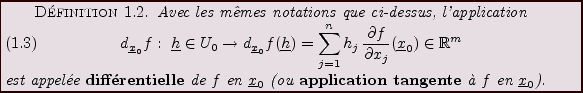
REMARQUE 1.1 On note généralement
l'application ``projection'' sur la
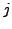
-ième composante.
On montre facilement que pour tout
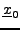
,
de sorte que l'on peut noter
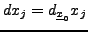
, et ainsi
écrire la différentielle de

sous la forme classique
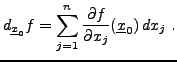 |
(1.3) |
EXEMPLE 1.1 On considère une fonction continue
![$ f: [a,b]\to{\mathbb{R}}$](img23.png)
, et la
fonction
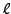
qui à
![$ x\in [a,b]$](img25.png)
associe la longueur
de la courbe définie par le graphe de

.
La différentielle en
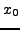
de
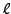
vaut
et le théorème de Pythagore montre que
d'où
On en déduit l'expression de la fonction
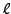
:
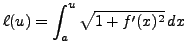 |
(1.4) |
et la longueur
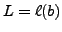
de la courbe.

La différentielle et la matrice Jacobienne possèdent d'importantes
propriétés vis à vis de la composition des fonctions.
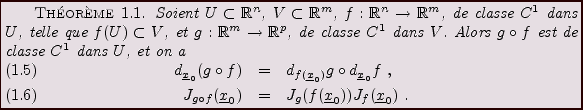
Les dérivées d'ordre supérieur sont définies récursivement.
Par exemple, étant donnée une fonction de plusieurs variables
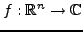 , on définit
, on définit
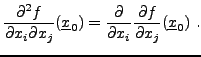 |
(1.5) |
Pour des dérivées d'ordres peu élevés, on utilisera
également la notation suivante
Le résultat essentiel est le théorème de Schwarz
![\begin{theorem}[Schwarz]
Soit $U\subset{\mathbb{R}}^n$, soit ${\underline{x}}_0\...
...^2f}{\partial x_j\partial x_i}({\underline{x}}_0)\ .
\end{equation}\end{theorem}](img37.png)

Optimiser une fonction de plusieurs variables équivaut à en
chercher les extrêma, c'est à dire les maxima et les minima.

Une notion centrale pour la recherche d'extrêma locaux est
la notion de point critique.
On dit que
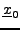 est un point critique de la fonction
est un point critique de la fonction  (supposée de classe
(supposée de classe 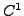 dans un voisinage de
dans un voisinage de
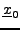 ) si
pour tout
) si
pour tout
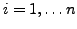 , on a
, on a
ce que l'on note
Les points critiques caractérisent les extrêma locaux d'une fonction
 à l'ordre 1. Cependant, le gradient
à l'ordre 1. Cependant, le gradient 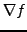 de
de  ne permet
pas de décider si un point critique est effectivement un extrêmum,
ni si il s'agit d'un minimum ou d'un maximum. Il est nécessaire pour
cela d'effectuer une étude à l'ordre deux. On utilise pour cela
le résultat suivant, qui étend la proposition
ne permet
pas de décider si un point critique est effectivement un extrêmum,
ni si il s'agit d'un minimum ou d'un maximum. Il est nécessaire pour
cela d'effectuer une étude à l'ordre deux. On utilise pour cela
le résultat suivant, qui étend la proposition ![[*]](crossref.png)
![\begin{theorem}[Taylor-Young]
Soient $U\subset{\mathbb{R}}^n$, ${\underline{x}}_...
...\lim_{\vert{\underline{h}}\vert\to 0}\epsilon({\underline{h}})=0$.
\end{theorem}](img45.png)
Le terme de second ordre dans le théorème ci-dessus fait intervenir
la Matrice Hessienne (ou Hessienne) de  en
en
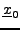 :
:
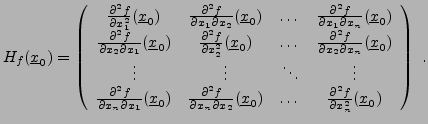 |
(1.6) |
La matrice Hessienne est réelle symétrique, elle est
donc diagonalisable. Ses valeurs propres (qui sont réelles)
possèdent une interprétation simple.

Notons que si certaines valeurs propres de
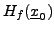 sont nulles,
il n'est pas possible de conclure.
sont nulles,
il n'est pas possible de conclure.
EXEMPLE 1.2 Soit
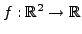
, définie par
On a
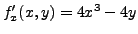
et
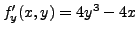
. Ainsi les
points critiques
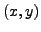
satisfont nécessairement
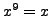
et
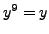
, d'où les trois solutions
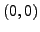
,

et
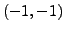
. La matrice Hessienne est de la forme
On en déduit aisément que
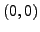
est un minimum local,
alors que

et
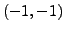
sont des points selle.
EXEMPLE 1.3 Lois de Snell-Descartes en deux dimensions.
Un rayon lumineux se propage à la vitesse
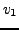
dans le
milieu 1 (demi-plan supérieur dans la F
IG. ![[*]](crossref.png)
),
et à la vitesse
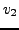
dans le milieu 2 (demi-plan inférieur).
Le principe de Fermat
précise
que la lumière suit le trajet
le plus économique en temps. En notant
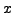
l'abscisse du point
où la trajectoire coupe l'interface, le temps nécessaire pour
aller de
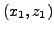
à
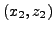
en passant par le point
d'abscisse
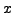
vaut
Cette quantité est (localement) optimale quand sa dérivée par rapport
à
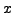
s'annule, c'est à dire lorsque
ce qui conduit à la loi de Snell-Descartes
Figure:
Loi de Snell-Descartes
|
|
On obtient de la même façon la loi de Snell-Descartes
à la réflexion.
EXEMPLE 1.4 Lois de Snell-Descartes en trois dimensions.
Dans le cas tridimensionnel, la situation est similaire. Il s'agit
cette fois de déterminer les coordonnées
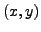
dans le plan
de l'interface où le rayon coupera celui-ci. Le temps de trajet
vaut cette fois
Il s'agit cette fois d'optimiser par rapport à
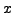
et
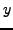
simultanément, ce
qui revient à annuler simultanément les dérivées de

par
rapport à
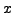
et
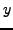
, c'est à dire son gradient bidimensionnel.
Ceci conduit aux équations
qui impliquent immédiatement
i.e. le point du plan de coordonnées
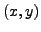
se trouve dans
le segment compris entre
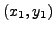
et
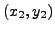
. On se ramène donc à un problème bidimensionnel, et
le raisonnement ci-dessus s'applique directement.
Optimisation sous contrainte
Il arrive que l'on ait à rechercher des extrêma de certaines
fonctions de plusieurs variables, auxquelles sont imposées
un certain nombre de contraintes supplémentaires.
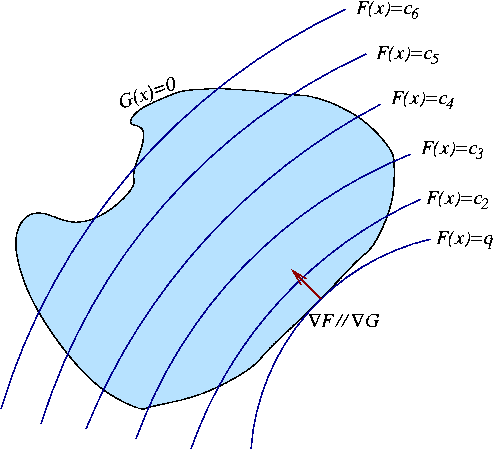
On a dans ce cas recours à la méthode des multiplicateurs
de Lagrange, qui est illustrée en FIG. ![[*]](crossref.png) dans un exemple bidimensionnel.
Dans cet exemple, on cherche à minimiser une certaine
fonction
dans un exemple bidimensionnel.
Dans cet exemple, on cherche à minimiser une certaine
fonction 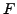 définie sur le plan,
dont les lignes de niveau sont tracées en courbes (presque
parallèles sur la figure), sous une contrainte prenant la forme
définie sur le plan,
dont les lignes de niveau sont tracées en courbes (presque
parallèles sur la figure), sous une contrainte prenant la forme
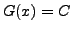 (une constante), représentée comme le bord
d'un domaine sur la figure).
Il apparaît clairement que l'optimum est obtenu lorsque les gradients de
(une constante), représentée comme le bord
d'un domaine sur la figure).
Il apparaît clairement que l'optimum est obtenu lorsque les gradients de
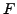 et
et 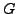 sont confondus.
sont confondus.
Figure:
Optimisation sous contrainte par multiplicateurs de Lagrange:
les lignes sont les lignes de niveau de la fonction
à optimiser, et la contrainte est représentée par
le bord de la surface fermée.
|
|
Cet exemple peut se généraliser en dimension quelconque, où il
prend une forme tout à fait similaire.
Plus précisément, le résultat général est le suivant:

Bruno Torresani
2007-06-26
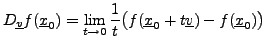
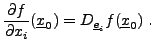
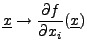
![]()
![\begin{proposition}[Taylor]
Soit $f:{\mathbb{R}}^n\to{\mathbb{R}}^m$, de classe ...
...erline{h}}\to 0}\epsilon({\underline{h}}) = 0\ .
\end{equation}\end{proposition}](img16.png)
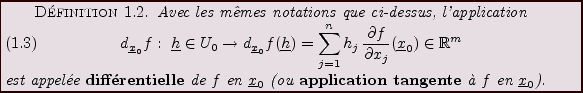
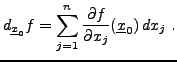
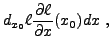
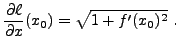
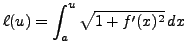

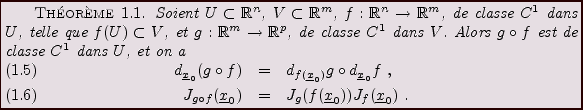
![]() , on définit
, on définit
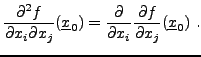
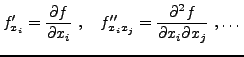
![\begin{theorem}[Schwarz]
Soit $U\subset{\mathbb{R}}^n$, soit ${\underline{x}}_0\...
...^2f}{\partial x_j\partial x_i}({\underline{x}}_0)\ .
\end{equation}\end{theorem}](img37.png)


![]() est un point critique de la fonction
est un point critique de la fonction ![]() (supposée de classe
(supposée de classe ![]() dans un voisinage de
dans un voisinage de
![]() ) si
pour tout
) si
pour tout
![]() , on a
, on a

![[*]](crossref.png)
![\begin{theorem}[Taylor-Young]
Soient $U\subset{\mathbb{R}}^n$, ${\underline{x}}_...
...\lim_{\vert{\underline{h}}\vert\to 0}\epsilon({\underline{h}})=0$.
\end{theorem}](img45.png)
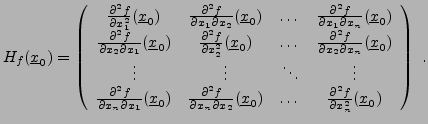

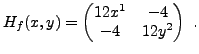
![[*]](crossref.png) ),
et à la vitesse
),
et à la vitesse 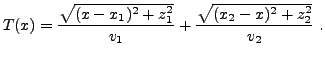
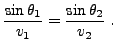
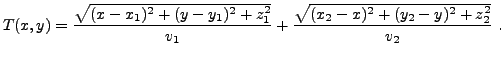
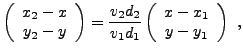
![[*]](crossref.png) dans un exemple bidimensionnel.
Dans cet exemple, on cherche à minimiser une certaine
fonction
dans un exemple bidimensionnel.
Dans cet exemple, on cherche à minimiser une certaine
fonction