Next: Quelques exemples... et contre-exemples Up: Calcul des variations Previous: Dérivation, optimisation
c'est à dire d'applications associant une valeur numérique à une ou plusieurs fonctions
On part du cas simple d'une fonctionnelle ![]() , dépendant
des valeurs d'une unique fonction recherchée
, dépendant
des valeurs d'une unique fonction recherchée ![]() et sa dérivée
et sa dérivée ![]() ,
sous la forme
,
sous la forme
Le problème posé est de trouver la fonction ![]() telle que
le nombre
telle que
le nombre ![]() soit minimal (ou maximal), sous contrainte que les
valeurs de
soit minimal (ou maximal), sous contrainte que les
valeurs de ![]() aux bords
aux bords ![]() et
et ![]() soient fixées.
Dans le cas de des fonctions de plusieurs variables,
rechercher les extrêma d'une fonction revient à chercher les points où
la dérivée s'annule. C'est cette notion qu'il nous faut généraliser
au cas des fonctionnelles. Nous allons rechercher les fonctions
soient fixées.
Dans le cas de des fonctions de plusieurs variables,
rechercher les extrêma d'une fonction revient à chercher les points où
la dérivée s'annule. C'est cette notion qu'il nous faut généraliser
au cas des fonctionnelles. Nous allons rechercher les fonctions ![]() telles que
telles que ![]() ne varie pas lorsque l'on varie
ne varie pas lorsque l'on varie ![]() de façon
infinitésimale, dans une ``direction'' quelconque.
de façon
infinitésimale, dans une ``direction'' quelconque.
Etudier les variations de ![]() dans une ``direction''
dans une ``direction'' ![]() (ici,
(ici, ![]() est
donc une fonction) donnée revient à étudier la quantité
(la variation)
est
donc une fonction) donnée revient à étudier la quantité
(la variation)
![$\displaystyle D_g f = \left(\frac{d}{d\epsilon} \Phi[f+\epsilon g]\right)_{\epsilon=0} =
\lim_{\epsilon\to 0} \frac{\Phi(f+\epsilon g) - \Phi(f)}{\epsilon}
$](img95.png)
On se limite aux fonctions
Un calcul formel montre que ceci revient à écrire
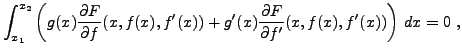
et une intégration par parties conduit à

On utilise ici la version unidimensionnalle du Lemme fondamental du calcul variationnel


reliant
![$\displaystyle {\mathcal L}[y] = \int_{x_1}^{x_2} \sqrt{1+y'(x)^2}\,dx\ ,
$](img106.png)
c'est à dire
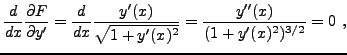
ce qui implique
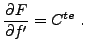
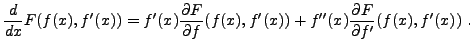
L'équation d'Euler-Lagrange implique alors que
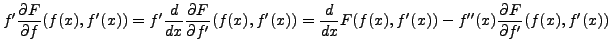
d'où
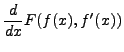 |
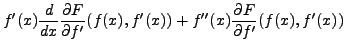 |
||
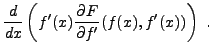 |

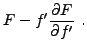
Par exemple, dans le cas de l'application à la mécanique Hamiltonienne, nous verrons que lorsque le Lagrangien ne dépend pas explicitement du temps (qui est alors la variable indépendante), il existe une quantité conservée, le Hamiltonien, qui représente en fait l'énergie du système considéré.
Bruno Torresani 2007-06-26