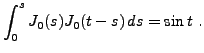Next: Propriétés de régularité Up: La transformation de Laplace Previous: Propriétés élémentaires
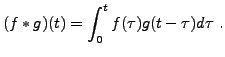 |
(4.1) |

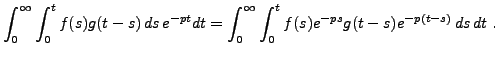
Un changement de variables
![[*]](crossref.png) ), à condition que
), à condition que Ce résultat trouvera son intérêt quand on considèrera la transformation de Laplace inverse. Cette propriété est aussi utile pour évaluer certaines intégrales, comme le montre l'exemple suivant.