Subsections
Propriétés de régularité
L'un des intérêts de la transformation de Laplace est que dans le
domaine où elle est définie, elle est holomorphe. Ceci permet
alors d'utiliser des techniques d'intégration dans le plan
complexe, en particulier pour le calcul de la transformation de
Laplace inverse que nous allons voir plus bas.
Plus précisément, on a le résultat suivant:

Preuve:
Commençons par étudier l'abscisse d'intégrabilité de la
fonction
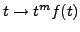 , noté
, noté 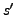 .
Pour
.
Pour 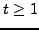 , on a
, on a
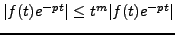 .
Donc l'intégrabilité de
.
Donc l'intégrabilité de
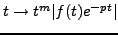 dans
dans
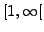 implique l'intégrabilité de
implique l'intégrabilité de
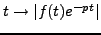 dans
dans
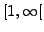 ,
et donc dans
,
et donc dans
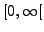 . Par conséquent, on a
. Par conséquent, on a 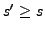 .
.
Inversement, pour tout
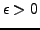 , on peut toujours trouver
, on peut toujours trouver 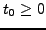 tel que pour tout
tel que pour tout 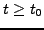 , on ait
, on ait
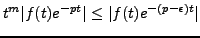 . L'argument précédent montre donc que
pour tout
. L'argument précédent montre donc que
pour tout
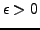 , on a
, on a
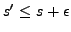 . Par conséquent,
. Par conséquent, 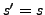 .
.
On peut donc dériver sous le signe somme, et on obtient bel et bien
l'expression voulue. L'holomorphie est donnée par le case 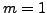 .
.
EXEMPLE 4.2 Reprenons le cas particulier de la fonction
Cette fonction n'admet pas de transformée de Fourier dans le sens usuel
(la théorie des distributions permet d'en définir une), mais possède
une transformée de Laplace. Un calcul explicite donne
à condition de se limiter à
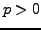
(c'est à dire que l'on a
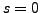
). La fonction que l'on obtient est bien holomorphe dans
le demi-plan (ouvert)
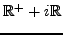
. Par contre, noter les deux
pôles en
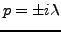
.
REMARQUE 4.1 L'exemple précédent est aussi intéressant pour la raison suivante.
La fonction
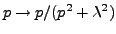
est en fait bien définie dès
que
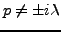
. Cependant, cette fonction n'est transformée
de Laplace de
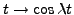
que dans le domaine ouvert
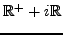
(la TL n'étant pas définie ailleurs). Dans le
reste du plan complexe (privé de
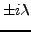
bien sûr), elle
n'est que le prolongement analytique de la TL du cosinus.
Nous avons déjà vu que la transformation de Fourier se
comporte de façon remarquable vis à vis des opérateurs
différentiels (ce qui ètait d'ailleurs le point de départ
du travail de J. Fourier). La transformation de Laplace possède des
propriétés similaires, à une petite différence près,
qui vient du fait que l'on ne travaille que sur le demi axe réel
positif4.1: les valeurs de  et ses dérivées
à l'origine interviennent, comme conséquence d'intégrations
par parties successives. Pour cela, il faut que ces valeurs
soient définies, ce qui suppose des hypothèses de régularité
sur la fonction étudiée.
et ses dérivées
à l'origine interviennent, comme conséquence d'intégrations
par parties successives. Pour cela, il faut que ces valeurs
soient définies, ce qui suppose des hypothèses de régularité
sur la fonction étudiée.

Preuve :
Commençons par le cas 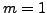 . Il suffit de calculer, pour
. Il suffit de calculer, pour 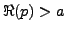 ,
,
La disparition du terme tout intégré évalué en 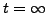 résulte de (
résulte de (![[*]](crossref.png) ), et du fait que
), et du fait que 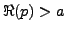 .
Pour
.
Pour 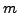 quelconque, il suffit d'itérer comme suit
quelconque, il suffit d'itérer comme suit
qui donne (![[*]](crossref.png) ) par récurrence. Ceci conclut la preuve.
) par récurrence. Ceci conclut la preuve.
Cette dernière propriété est souvent utilisée pour la
résolution d'équations différentielles ou d'équations
aux dérivées partielles.
EXEMPLE 4.3 Prenons l'exemple de l'équation de Poisson
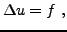 |
(4.2) |
où

est un second membre fixé, et
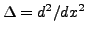
est le Laplacien unidimensionnel. Pour obtenir une solution unique,
on sait qu'il est nécessaire de faire des hypothèses
supplémentaires, et d'adjoindre à cette équation deux
conditions additionnelles.
On suppose donc que
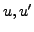
et

satisfont
la condition (
![[*]](crossref.png)
) (il est
possible de démontrer dans un cadre plus général l'existence de
solutions satisfaisant à de telles conditions), et que

et
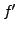
sont continues.
Supposons aussi par exemple que
où
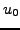
et
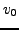
sont deux nombres fixés.
On note
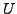
la transformée de Laplace de
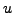
, et
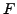
la
transformée de Laplace de

. Les hypothèses faites
assurent l'existence (et l'analyticité) de
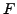
dans un domaine
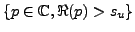
, avec
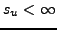
.
on se ramène alors à
soit encore, pour
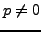
,
dans un domaine de valeurs de
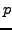
bien choisi: la fonction
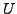
ainsi obtenue est analytique dans le domaine
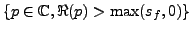
.
Cette équation permet d'obtenir une solution
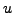
à partir de

, par
transformation de Laplace inverse (que nous verrons plus loin).
On peut toutefois utiliser ce que l'on sait déjà, c'est à
dire les propriétés de linéarité de la transformation de Laplace,
sa relation avec le produit de convolution ainsi que les quelques
transformées de Laplace déjà vues.
Ainsi, on sait que l'oiginal de Laplace de la fonction 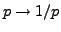 est
la fonction de Heaviside
est
la fonction de Heaviside 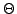 , et que l'original de Laplace de
, et que l'original de Laplace de
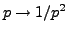 est la fonction
est la fonction
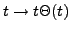 . Par ailleurs,
l'original de Laplace de la fonction
. Par ailleurs,
l'original de Laplace de la fonction
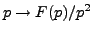 est le produit de
convolution de
est le produit de
convolution de  par la fonction
par la fonction
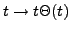 . On en déduit donc
. On en déduit donc

Preuve:
Il résulte des hypothèses que l'abscisse d'intégrabilité 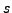 de
de  est tel que
est tel que  . Comme
. Comme
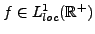 ,
, 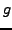 est
continue et dérivable, et on a aussi, pour tout
est
continue et dérivable, et on a aussi, pour tout 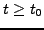 ,
,
pour une certaine constante positive  . Il suffit alors d'appliquer le
théorème précédent, qui donne
. Il suffit alors d'appliquer le
théorème précédent, qui donne
et ceci prouve la proposition.
Bruno Torresani
2007-06-26

![]() , noté
, noté ![]() .
Pour
.
Pour ![]() , on a
, on a
![]() .
Donc l'intégrabilité de
.
Donc l'intégrabilité de
![]() dans
dans
![]() implique l'intégrabilité de
implique l'intégrabilité de
![]() dans
dans
![]() ,
et donc dans
,
et donc dans
![]() . Par conséquent, on a
. Par conséquent, on a ![]() .
.
![]() , on peut toujours trouver
, on peut toujours trouver ![]() tel que pour tout
tel que pour tout ![]() , on ait
, on ait
![]() . L'argument précédent montre donc que
pour tout
. L'argument précédent montre donc que
pour tout
![]() , on a
, on a
![]() . Par conséquent,
. Par conséquent, ![]() .
.
![]() .
.
![]()
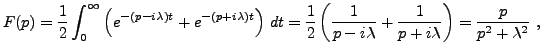

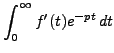
![$\displaystyle \left[f(t)e^{-pt} \right]_0^\infty + p\int_0^\infty f'(t)e^{-pt}\,dt$](img980.png)
![[*]](crossref.png) ), et du fait que
), et du fait que ![[*]](crossref.png) ) par récurrence. Ceci conclut la preuve.
) par récurrence. Ceci conclut la preuve.
![[*]](crossref.png) ) (il est
possible de démontrer dans un cadre plus général l'existence de
solutions satisfaisant à de telles conditions), et que
) (il est
possible de démontrer dans un cadre plus général l'existence de
solutions satisfaisant à de telles conditions), et que
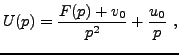
![]() est
la fonction de Heaviside
est
la fonction de Heaviside ![]() , et que l'original de Laplace de
, et que l'original de Laplace de
![]() est la fonction
est la fonction
![]() . Par ailleurs,
l'original de Laplace de la fonction
. Par ailleurs,
l'original de Laplace de la fonction
![]() est le produit de
convolution de
est le produit de
convolution de ![]() par la fonction
par la fonction
![]() . On en déduit donc
. On en déduit donc
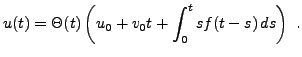

![]() de
de ![]() est tel que
est tel que ![]() . Comme
. Comme
![]() ,
, ![]() est
continue et dérivable, et on a aussi, pour tout
est
continue et dérivable, et on a aussi, pour tout ![]() ,
,