Next: La transformation de Laplace Up: La transformation de Laplace Previous: Propriétés de régularité
Une première approche possible consiste à utiliser certaines expressions connues pour les transformées de Laplace de certaines fonctions élémentaires, comme on va le voir dans l'exemple suivant.
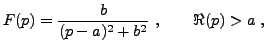
où
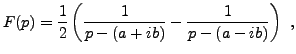
et ces deux termes sont transformées de Laplace de fonctions connues. On en déduit donc directement
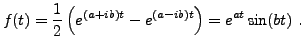
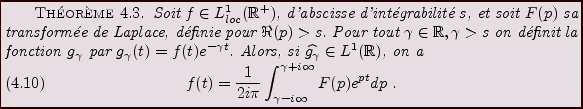
Preuve:
Le résultat est une conséquence de la relation entre transformation
de Laplace et transformation de Fourier. Soit
![]() ,
, ![]() ,
et soit
,
et soit
![]() . Si
. Si
![]() , alors on a
, alors on a
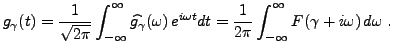
En utilisant l'holomorphie de
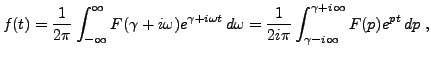
ce qui est le résultat désiré.
Par conséquent, on fait généralement appel à la formule des résidus pour évaluer une transformée de Laplace inverse.
|
EXEMPLE ![[*]](crossref.png) (SUITE)
Reprenons l'exemple de la fonction
(SUITE)
Reprenons l'exemple de la fonction ![]() dont la transformée de Laplace est
donnée par
dont la transformée de Laplace est
donnée par
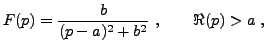
où
![[*]](crossref.png) ,
où
,
où
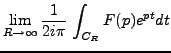 |
|||
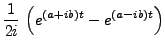 |
|||
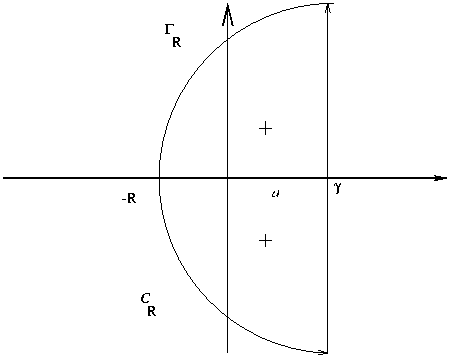
Dans ce type de problème, l'intégrale sur l'arc
de cercle ![]() tend vers 0 lorsque
tend vers 0 lorsque
![]() . On peut
soit vérifier ceci directement, soit invoquer des conditions
suffisantes sur la transformée de Laplace
. On peut
soit vérifier ceci directement, soit invoquer des conditions
suffisantes sur la transformée de Laplace ![]() assurant que
cette intégrale tend réellement vers 0. Une telle condition
a été donnée par Carslaw et Jaeger:
assurant que
cette intégrale tend réellement vers 0. Une telle condition
a été donnée par Carslaw et Jaeger:
![\begin{lemma}[Carslaw et Jaeger]
Si il existe des constantes positives $C>0$, $R...
...t\'egrale sur le contour $\Gamma_R$\ tend
vers 0 quand $R\to\infty$.
\end{lemma}](img1014.png)
![[*]](crossref.png) ci dessous.
ci dessous.
L'évolution spatio-temporelle de ce champ ![]() est régie par
l'équation de la chaleur
est régie par
l'équation de la chaleur
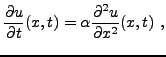 |
(4.3) |
| (4.4) | |||
| (4.5) |
![[*]](crossref.png) )), ce qui
nous assure de pouvoir utiliser les résultats de la Proposition
)), ce qui
nous assure de pouvoir utiliser les résultats de la Proposition ![[*]](crossref.png) .
Par transformation de Laplace (par rapport à la variable
.
Par transformation de Laplace (par rapport à la variable 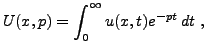 |
(4.6) |
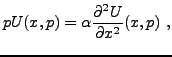 |
(4.7) |
Si l'on impose à la solution d'être bornée quand
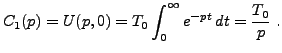
Donc,
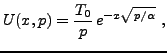 |
(4.8) |
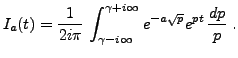 |
(4.9) |

|
Considérons le contour ![]() (voir FIG.
(voir FIG. ![[*]](crossref.png) ).
L'intégrand étant holomorphe à
l'intérieur de
).
L'intégrand étant holomorphe à
l'intérieur de ![]() , l'intégrale sur
, l'intégrale sur ![]() est nulle, de sorte
que l'on peut écrire
est nulle, de sorte
que l'on peut écrire
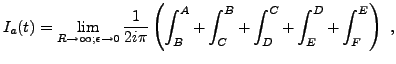
et il faut maintenant évaluer chacun des termes.
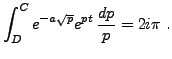
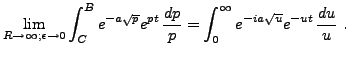
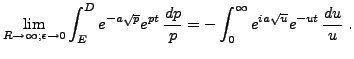
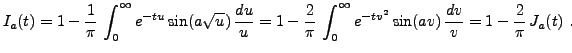
Pour finir, on remarque que
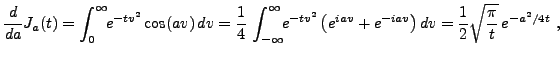
de sorte que
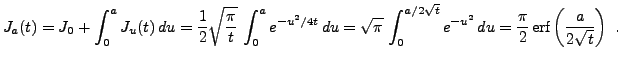
On en déduit l'intégrale recherchée
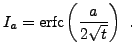
Donc, la solution est finalement
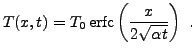 |
(4.10) |
![[*]](crossref.png) .
.
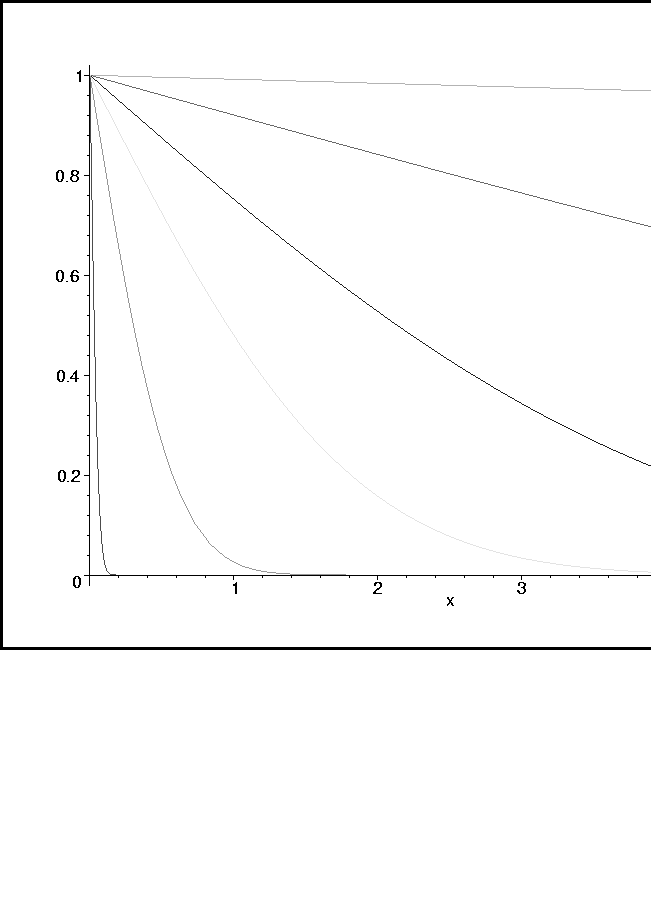
|
Bruno Torresani 2007-06-26