La transformation de Laplace bilatérale

La transformée de Laplace bilatérale s'adresse aux fonctions définies sur la droite réelle, et non plus sur la demi droite. Le cadre mathématique approprié est le cadre des fonctions localement intégrables sur l'axe réel $L^1_{loc}({\mathbb{R}})$ .
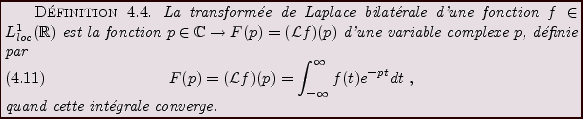
$\begin{definition} La transform\'ee de Laplace bilat\'erale d'une fonction $f\in... ...) e^{-pt} dt\ , \end{equation}quand cette int\'egrale converge. \end{definition}$

La transformation de Laplace bilatérale possède des propriétés très semblables à celles de la transformation de Laplace unilatérale. La différence essentielle vient de leurs domaines de définition respectifs.

Supposons que pour deux nombres réels et , avec la fonction $t\to e^{-pt}f(t)$ soit intégrable pour $\Re(p)=x_0$ et $\Re(p)=x_1$ . Alors, on voit immédiatement que cette fonction est également intégrable pour tout tel que $x_0\le\Re(p)\le x_1$ . En notant et le minimum et le maximum respectivement des valeurs de et telles que la propriété précédente soit vraie, on aboutit au résultat suivant, qui généralise le cas unilatéral.
$\begin{theorem} \begin{enumerate} \item Soit $f\in L^1_{loc}({\mathbb{R}})$. Il ... ...s le domaine $p\in\mathbb{C}, \Re(p)\in ]s_0,s_1[$. \end{enumerate}\end{theorem}$

Les propriétés essentielles de la transformation de Laplace bilatérale sont essentiellement des paraphrases des propriétés que nous avons vues dans le cas unilatéral. On ne s'étendra pas sur ces propriétés. On insistera plutôt sur deux propriétés importantes, c'est à dire la forme de la transformée de Laplace d'une dérivée, et la formule d'inversion.

$\begin{proposition} Soit $f\in C^{m-1}({\mathbb{R}})$, telle que sa d\'eriv\'ee ... ...equation} ({\mathcal L}f^{(m)})(p) = p^m F(p)\ . \end{equation}\end{proposition}$

La formule d'inversion quant à elle est comme dans le cas unilatéral une conséquence de la formule d'inversion de la transformée de Fourier.
$\begin{theorem} Soit $f\in C^{m-1}({\mathbb{R}})$, et soit $D_f =\{p\in\mathbb{C... ...{\gamma-i\infty}^{\gamma+i\infty} F(p) e^{pt}\,dp\ . \end{equation}\end{theorem}$
Les transformées de Laplace bilatérales inverses se calculent généralement en utilisant la méthode des résidus.

Bruno Torresani 2007-06-26