Subsections
La notion essentielle pour la théorie des distributions
est la notion de dualité.

Un espace des distributions sera le dual,
dans un sens que nous allons voir, d'un espace vectoriel de
fonctions bien choisi, que l'on appellera espace de fonctions test.
On verra dans ce qui suit différents espaces de fonctions test.
Les distributions sont donc définies par dualité, en considérant
pour espace fonctionnel 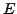 l'espace des fonctions
l'espace des fonctions 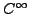 à
support compact.
à
support compact.
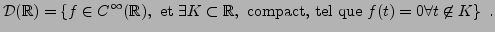 |
(5.1) |
Pour construire le dual
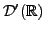 de
de
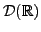 , il faut définir
ce que l'on entend par convergence au sens de
, il faut définir
ce que l'on entend par convergence au sens de
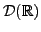 . On dira
qu'une suite de fonctions
. On dira
qu'une suite de fonctions
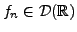 converge vers
converge vers
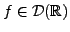 si
si
- il existe un compact
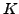 tel que le support de
tel que le support de 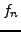 soit contenu dans
soit contenu dans 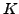 pour tout
pour tout 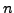 .
.
- Pour tout
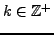 , la suite des dérivées
, la suite des dérivées 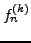 converge
uniformément vers
converge
uniformément vers 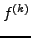 .
.

EXEMPLE 5.1 L'exemple le plus simple est celui de la distribution nulle:
Les propriétés de linéarité et continuité sont vérifiées
facilement.
EXEMPLE 5.2 La
distribution de Dirac

, où
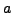
est un réel
quelconque, est définie de la façon suivante: pour toute
fonction de test
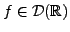
,
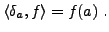 |
(5.2) |
EXEMPLE 5.3 Le
peigne de Dirac, noté
(lettre de l'alphabet cyrillique), associe
à toute fonction test la somme de la série de ses échantillons
(ou valeurs ponctuelles) régulièrement espacés.
Comme

est supposée à support compact, cette série est automatiquement
convergente (car finie).
Le peigne de Dirac s'exprime comme
En quoi les distributions sont elles des généralisations
des fonctions ? on va voir que l'espace
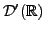 contient l'espace
contient l'espace
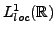 ... dans
un certain sens, qu'on va maintenant préciser. Rappelons
tout d'abord qu'en notant
l'indicatrice
d'un domaine
:
... dans
un certain sens, qu'on va maintenant préciser. Rappelons
tout d'abord qu'en notant
l'indicatrice
d'un domaine
:
on définit
A toute fonction de
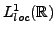 on peut associer une
distribution de la façon suivante.
Soit
. Soit
l'application définie par
on peut associer une
distribution de la façon suivante.
Soit
. Soit
l'application définie par
Comme
, cette intégrale est absolument convergente.
De plus, il est immédiat de vérifier que
est une
forme linéaire sur
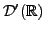 . Le point le plus délicat à
vérifier est la continuité de
.
. Le point le plus délicat à
vérifier est la continuité de
.
Ainsi, à toute fonction localement intégrable  , on peut associer
une distribution, appelée distribution
régulière
.
, on peut associer
une distribution, appelée distribution
régulière
.
REMARQUE 5.1 En pratique, on note souvent (abusivement)

la distribution
régulière
associée à

(et on dit donc
, par abus de notation, au lieu de
).
Ainsi, on note parfois une distribution
sous la même forme qu'une fonction
, et on écrit alors
Par exemple, on associe à la distribution de Dirac une
``fonction généralisée'', notée
, qui a
la propriété que pour toute
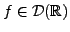
Avec ces notations, on peut donc noter
de sorte que l'on écrit
Dans ce qui suit, on essaie au maximum d'éviter de recourir
à ce type de notation, qui est cependant parfois plus pratique
pour effectuer des calculs.
Soit
. Le produit de 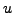 par une fonction
par une fonction
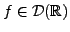 est toujours une fonction
.
On a donc
est toujours une fonction
.
On a donc
EXEMPLE 5.4 Etant donnée la distribution de Dirac

, et
, on a
de sorte que l'on a l'égalité suivante, au sens des distributions
REMARQUE 5.2 Alors que le produit d'une distribution
par
une fonction
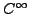
est bien définie, le produit d'une
distribution par une autre distribution n'a généralement pas de
sens, c'est à dire ne définit par une nouvelle distribution.
Par exemple, le produit
n'a pas de sens.
On considère l'opérateur parité,
défini par
L'action de cet opérateur sur des distributions se définit de
la façon suivante. Etant donnée
, on note
, la distribution définie par
On rappelle qu'une fonction  est paire si
, et impaire
si
.
est paire si
, et impaire
si
.
Il est clair que pour toute fonction paire, la distribution régulière
associée est paire:
De même la distribution associée à une fonction impaire est impaire.
Par exemple, on vérifie que la distribution de Dirac 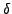 est
paire, alors que sa dérivée
est impaire.
est
paire, alors que sa dérivée
est impaire.
Soit
l'opérateur de
translation par
, défini
par
Une fonction  est périodique de période
est périodique de période 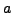 si
. On définit la translatée
d'une distribution
par
si
. On définit la translatée
d'une distribution
par
On vérifie facilement que le peigne de Dirac
est
périodique de période  .
.
Bruno Torresani
2007-06-26


![]() contient l'espace
contient l'espace
![]() ... dans
un certain sens, qu'on va maintenant préciser. Rappelons
tout d'abord qu'en notant
l'indicatrice
d'un domaine
:
... dans
un certain sens, qu'on va maintenant préciser. Rappelons
tout d'abord qu'en notant
l'indicatrice
d'un domaine
:
![]() on peut associer une
distribution de la façon suivante.
Soit
. Soit
l'application définie par
on peut associer une
distribution de la façon suivante.
Soit
. Soit
l'application définie par
![]() , on peut associer
une distribution, appelée distribution
régulière
.
, on peut associer
une distribution, appelée distribution
régulière
.
![]() est
paire, alors que sa dérivée
est impaire.
est
paire, alors que sa dérivée
est impaire.