Next: Distributions: définition, propriétés et Up: MATHÉMATIQUE POUR LA PHYSIQUE Previous: Formulaire
La théorie des distributions, développée en
mathématiques par I.M. Gelfand, puis par L. Schwartz,
trouve ses origines dans certains problèmes de physiques.
Comme motivation on cite généralement le probléme du calcul
du potentiel généré par une ``distribution'' de charge. Lorsque
ces charges sont des charges ponctuelles, situées en des points
![]() , le potentiel créé en un point
, le potentiel créé en un point
![]() s'écrit
s'écrit
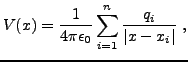
où
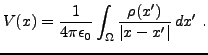
Dans le cas le plus général, on est amené à considérer simultanément ces différents cas, ce qui complique le formalisme. La théorie des distributions permet de donner une approche unifiée pour ces situations.
Le but de la théorie des distributions est de permettre d'étendre des opérations ``classiques'' sur les fonctions, telles que dérivation, intégration, convolution, transformations de Fourier, à des cadres dans lesquels ces opérations ne sont a priori pas définies.
L'exemple le plus simple est celui de la fonction ``saut'',
ou fonction de Heaviside
![]() . Cette fonction, bien que très simple, est
difficile à appréhender dans un cadre de calcul intégral,
dans la mesure où elle ne tend pas vers zéro à l'infini. Elle
est également difficile à manipuler dans un cadre de calcul
différentiel, car elle est discontinue en
. Cette fonction, bien que très simple, est
difficile à appréhender dans un cadre de calcul intégral,
dans la mesure où elle ne tend pas vers zéro à l'infini. Elle
est également difficile à manipuler dans un cadre de calcul
différentiel, car elle est discontinue en ![]() .
.
Cependant, l'idée intuitive que l'on peut s'en faire est que
sa dérivée, si elle avait un sens, devrait être nulle pour tout
![]() , et ``infinie'' en
, et ``infinie'' en ![]() . Dirac a donc proposé de lui
associer une ``pseudo-fonction'' dérivée, notée
. Dirac a donc proposé de lui
associer une ``pseudo-fonction'' dérivée, notée ![]() ,
définie par un passage à la limite
,
définie par un passage à la limite
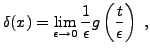
qui possède bien le comportement désiré. Ici,
On va voir que cette limite n'a pas de sens en tant que fonction usuelle; il s'agit d'une limite d'une suite de fonctions continues, qui ne définit néanmoins pas une fonction continue (puisqu'elle diverge en 0.
La théorie des distributions permet de donner un sens à ce type de limites, via l'introduction d'un concept assez élaboré, le concept de dual d'un espace fonctionnel.