On construit de même les distributions sur
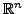 .
Il suffit d'introduire les espaces
des fonctions dont
toutes les dérivées sont continues, et
.
Il suffit d'introduire les espaces
des fonctions dont
toutes les dérivées sont continues, et
Comme en dimension 1, les exemples ne manquent pas. On définit par exemple
les distributions régulières de la même façon qu'en dimension 1:
en définissant l'espace des fonction localement intégrables
on associe à toute
la
distribution régulière
, définie par
Avec les mêmes précautions qu'en dimension 1, on a parfois tendance
à identifier une fonction localement intégrable
avec la
distribution régulière associée
... et à associer
à des distributions non régulières
une ``pseudo-fonction'', ou fonction généralisée, notée
, de sorte que l'on écrit
Là encore, il convient d'être très précautionneux
avec ce type de notation.
EXEMPLE 5.5 On considère la fonction de Heaviside unidimensionnelle
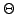
, et
on construit la fonction
suivante
Il s'agit d'une variante 3D de la fonction de Heaviside. Cette fonction
est localement intégrable, et permet donc de définir une
distribution régulière.
Soit maintenant
, définie par
(que l'ont note aussi
)
est l'indicatrice d'un quadrant de l'espace tridimensionnel, et
définit une distribution régulière.
EXEMPLE 5.6 Toujours dans
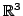
, la distribution de Dirac

, où
est définie de façon similaire à la distribution de Dirac
unidimensionnelle: pour
,
Cependant, il est aussi possible de définir des variantes à
la distribution de Dirac. Par exemple, étant donnée une surface
, la distribution de Dirac associée
est définie par
c'est à dire associe à toute fonction test son intégrale
sur la surface.
Ce type d'exemple est courant en physique, par exemple en
électrostatique, où on est couramment amené à considérer
des distributions de charge dite
superficielles.
On définit de façon similaire une distribution de Dirac
associée à une courbe
:
Plus généralement, on peut utiliser des distributions unidimensionnelles
pour construire des distributions multidimensionnelles, par la méthode
du produit tensoriel. Commençons par
le cas des distributions régulières.
Dans le cas bidimensionnel, soient
. On définit
par
Soit
la distribution régulière associée. On a alors,
pour
De façon générale, étant données
,  agissant
sur la variable
agissant
sur la variable 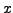 et
sur la variable
et
sur la variable 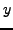 , on
définira
de la façon suivante: pour
toute
,
, on
définira
de la façon suivante: pour
toute
,
où par exemple
représente la dualité par rapport
à la variable 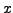 , et produit une fonction de
, et produit une fonction de 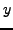 , et
représente cette fois la dualité
par rapport à la variable
, et
représente cette fois la dualité
par rapport à la variable 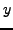 .
.
Bruno Torresani
2007-06-26
![]() agissant
sur la variable
agissant
sur la variable ![]() et
sur la variable
et
sur la variable ![]() , on
définira
de la façon suivante: pour
toute
,
, on
définira
de la façon suivante: pour
toute
,