Transformation de Fourier des distributions

La transformation de Fourier joue elle aussi un rôle fondamental, et la théorie des distributions permet de lui donner un sens dans des cas où la définition usuelle (au sens des fonctions) n'en a plus.

Espace de Schwartz et distributions tempérées

On peut facilement voir que toute fonction de 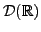${\mathcal D}({\mathbb{R}})$ appartient automatiquement à l'espace de Schwartz. De plus, toute fonction de est de carré intégrable. On a donc

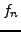Pour préciser la topologie de , il est nécessaire de définir la convergence dans . On dira qu'une suite de fonctions converge vers $f$ si pour tout , la suite des dérivées d'ordre de $f_n$ converge uniformément vers $f^{(k)}$ .

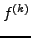On peut alors définir les distributions tempérées:

Comme conséquence des inclusions ci-dessus, on montre également les includsions inverses au niveau des espaces duaux:

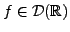
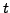
EXEMPLE 5.19   Les exemples les plus simples de distributions tempérées sont les distributions régulières. Cependant, toute distribution régulière n'est pas nécessairement tempérée. En effet, étant donnée , peut être bien définie pour toute fonction test $f\in{\mathcal D}({\mathbb{R}})$ , mais pas pour . Par exemple, en prenant pour tout $t$ , n'est pas bien défini pour une large classe de fonctions (par exemple ). Il est nécessaire de faire des hypothèses supplémentaires sur .

On dit que est à croissance lente si il existe 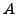$A$ , et tels que pour tout , on ait . On montre alors que les distributions régulières associées à de telles fonctions à croissance lente sont tempérées.

Par exemple, est une distribution tempérée.

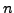
EXEMPLE 5.20   On montre facilement que toutes les distributions de Dirac et leurs dérivées sont des distributions tempérées. En effet, leur action sur les fonctions test de l'espace de Schwartz est bien définie. Par exemple, est bien défini pour tout entier $n$ si .

Il est possible de montrer pour les distributions tempérées un certain nombre de propriétés similaires à celles que nous avions rencontrées dans 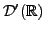${\mathcal D}'({\mathbb{R}})$ . Notamment

Transformée de Fourier des distributions tempérées

On rappelle la propriété centrale de la transformation de Fourier des fonctions, appelée formule d'échange: pour toutes fonctions , on a

La transformation de Fourier des distributions généralise cette propriété aux distributions tempérées.

EXEMPLE 5.21   Distributions de Dirac. Calculons : pour toute fonction test ,

Par conséquent, la transformée de Fourier de la distribution de Dirac est, à une constante près, la distribution régulière associée à la fonction identiquement égale à 1:

De même, pour tout ,

d'où on déduit

où est la sinusoïde

EXEMPLE 5.22   Sinusoïdes. Calculons tout d'abord

d'après la formule d'inversion de Fourier, qui s'applique (point par point) pour les fonctions de . On a donc

Si on prend le parti de noter les distributions sous forme de fonction généralisée, on notera alors

d'où la formule suivante, extrêmement utile dans les calculs:

De même, on montre facilement que

que l'on interprète aussi en termes de fonctions généralisées comme

Propriétés

La transformation de Fourier des distributions tempérées possède la plupart des propriétés ``standard'' de la transformation de Fourier des fonctions. On en donne une liste (non exhaustive) ci-dessous.

1. Linéarité. On vérifie facilement que pour tous et $\lambda\in\mathbb{C}$ ,
   

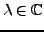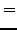   $$=$$ (5.30)

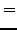   $$=$$ (5.31)

   
   
2. Comportement vis à vis des translations et modulations. Soit , et soit l'opérateur de translation par 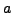$a$ : . En notant comme plus haut la fonction qui à tout associe , on a
   
   
   De même, en notant comme d'habitude le produit de la distribution (tempérée) par la fonction 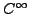$C^\infty$ ,
   
   

Transformation de Fourier et dérivation

Comme on l'a vu plus haut, l'espace de Schwartz ainsi que l'espace des distributions tempérées sont stables par dérivation. Par conséquent, étant donnée une distribution tempérée $T$ , à laquelle on sait associer sa transformée de Fourier , on sait également associer une transformée de Fourier à toutes ses dérivées, qui sont elles aussi dans .

Par ailleurs, on sait que pour toute fonction ,

$$=$$

$$=$$

où on a noté la fonction qui à 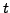$t$ associe .

Ecrivons donc, pour et tout

Ceci étant vrai pour tout , on a donc montré

Similairement, calculons

En étendant ces calculs aux dérivées d'ordres quelconques, on montre similairement

EXEMPLE 5.23   Dérivées de distributions de Dirac. En appliquant directement les expressions que nous venons de voir, et l'expression de la transformée de Fourier de distributions de Dirac, on obtient directement

Inversion de la transformation de Fourier

La transformation de Fourier des distributions tempérées hérite de la propriété d'inversibilité de la transformation de Fourier dans l'espace de Schwartz. En effet, si , alors est bien défini pour tout , et on a, pour tout ,

ce que l'on note

l'opérateur linéaire étant appelé transformée de Fourier conjuguée, ou transformée de Fourier adjointe. On peut donc noter

Ceci permet de définir la transformation de Fourier conjuguée des distributions tempérées: si , on définit sa transformée de Fourier conjuguée par dualité:

On voit alors facilement que pour tout et tout ,

d'après (), d'où on déduit

Ce résultat trouve de nombreuses applications, notamment pour la résolution d'équations différentielles, et d'équations aux dérivées partielles en dimensions supérieures.