Subsections
Le produit de convolution des fonctions (et des distributions) joue un rôle
fondamental en Physique. On va se limiter ici au cas des fonctions (et
distributions) d'une variable; la généralisation des définitions
au cas de plus d'une variable se fait assez simplement, mais certaines
propriétés et applications sont parfois bien plus complexes en dimensions
supérieures.
Rappelons tout d'abord la définition du produit de convolution
des fonctions. Etant données deux fonctions 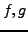 d'une variable
réelle, leur produit de convolution est la fonction
définie par
d'une variable
réelle, leur produit de convolution est la fonction
définie par
pour tout 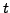 tel que l'intégrale converge.
Le produit de convolution possède des propriétés simples:
il est commutatif, et distributif par rapport à l'addition.
tel que l'intégrale converge.
Le produit de convolution possède des propriétés simples:
il est commutatif, et distributif par rapport à l'addition.
La notion de convolution joue un rôle fondamental en physique.
Elle intervient en particulier lorsqu'une quantité physique,
représentée par une fonction  , est mesurée à l'aide d'un
dispositif expérimental. Ce dernier est généralement
incapable de reproduire les fluctuations les plus rapides de
, est mesurée à l'aide d'un
dispositif expérimental. Ce dernier est généralement
incapable de reproduire les fluctuations les plus rapides de
 , et ne donne pour approximation de la valeur
en
, et ne donne pour approximation de la valeur
en 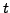 qu'une moyenne locale des valeurs de
qu'une moyenne locale des valeurs de  dans un voisinage
de
dans un voisinage
de 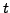 . On représente ceci via un produit de convolution
comme en (
. On représente ceci via un produit de convolution
comme en (![[*]](crossref.png) ), où la fonction
), où la fonction 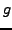 est une fonction localisée autour de 0
(de sorte que
est localisée autour de
), qui représente en
quelque sorte la réponse du dispositif expérimental.
est une fonction localisée autour de 0
(de sorte que
est localisée autour de
), qui représente en
quelque sorte la réponse du dispositif expérimental.
REMARQUE 5.3 Un dispositif expérimental parfait admettrait comme réponse
une fonction
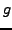
telle que
. Or il s'avère que
la réponse
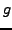
permettant ceci n'est autre que la distribution de Dirac:
Rappelons tout d'abord la notion de support d'une fonction. Par définition,
le support d'une fonction d'une variable réelle  est le plus petit
sous-ensemble fermé de
est le plus petit
sous-ensemble fermé de
 tel que
tel que  s'annulle en dehors de ce domaine.
Plus généralement, en dimension quelconque, étant donnée
s'annulle en dehors de ce domaine.
Plus généralement, en dimension quelconque, étant donnée
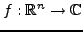 ,
,
la barre représentant la fermeture.
Ceci nous permet de donner un sens à
la notion de support d'une distribution.
Bien évidemment, le support d'une distribution régulière
coïncide avec le support de
.
EXEMPLE 5.13 Il est facile de vérifier que le support de la distribution de Dirac
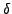
est le singleton
. De même, le support de

est
le singleton
. En dimension supérieure, le support de
la distribution
sur une courbe
de
est la courbe
elle-même.
Muni de cette définition, on peut alors introduire aussi les
notions suivantes
Comme d'habitude, la convolution des distributions s'obtient comme
généralisation de la convolution des distributions régulières.
Considérons donc
et les distributions
régulières associées. Alors,
, et on peut
considérer
: soit
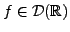 ,
,
où
est l'opérateur de translation
On reconnait dans l'intégrale sur 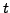 l'action de la distribution
régulière
sur
l'action de la distribution
régulière
sur 
qui produit donc une fonction de 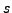 ; l'intégrale par rapport à
; l'intégrale par rapport à 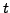 représente alors l'action de
sur cette fonction de
représente alors l'action de
sur cette fonction de 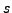 , ce
que l'on note
, ce
que l'on note
où on a aussi noté
la fonction
d'une variable réelle
Cette fonction possède la propriété suivante
Dans un cadre plus général, en définissant l'action d'un
opérateur de translation sur une distribution
par
on est conduit à définir de même la fonction
par
On peut alors introduire le produit de convolution de deux distributions:
Malgré cette définition quelque peu formelle, le produit de convolution
est relativement simple à utiliser, comme on le verra. En pratique,
on utilise souvent la notation des distributions comme fonctions
généralisées, ce qui permet de se débarrasser des notations
trop lourdes.
En fait, le produit de convolution de deux distributions données n'est
pas toujours bien défini. Il l'est toutefois au prix d'hypothèses
supplémentaires.
Alors, le produit de convolution possède les propriété suivantes:
- Il est commutatif:
- Il est distributif par rapport à l'addition:
- Il est associatif,
lorsque toutes ces opérations sont bien définies.
EXEMPLE 5.14 La distribution de Dirac est élément neutre pour le
produit de convolution:
Similairement, pour tout réel
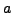
, on montre que
d'où, en appliquant cela au peigne de Dirac, on obtient pour tout
Cette distribution est appelée périodisée de

de période

.
L'utilisation des distributions pour la résolution
d'équations différentielles et équations aux dérivées partielles
repose essentiellement sur le résultat suivant:
Preuve:
Commençons par la première partie, et supposons que
existe. Alors
aussi, et
car la dérivation commute avec les translations. L'autre égalité se montre
de même. La preuve pour les dérivées de tous ordres est identique.
Pour la seconde partie, il suffit de remarquer que
cette démonstration se généralisant elle aussi à tous les ordres.
La conséquence immédiate de cette proposition est que les équations
différentielles au sens des distributions peuvent se mettre sous la forme
d'équations de convolution. Plus précisément, considérons une équation
différentielle d'ordre 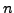 , de la forme
, de la forme
où les
sont des coefficients fixés, et le membre de droite
est lui aussi supposé connu. Cette équation se met sous la forme
où la distribution  est donnée par
est donnée par
La question est alors la suivante: peut on trouver un ``inverse'' à  pour
le produit de convolution. En d'autres termes, puisque comme on l'a vu, la
distribution de Dirac est élément neutre pour le produit de convolution,
existe-t-il une distribution, que l'on note
, telle que
pour
le produit de convolution. En d'autres termes, puisque comme on l'a vu, la
distribution de Dirac est élément neutre pour le produit de convolution,
existe-t-il une distribution, que l'on note
, telle que
Si tel est le cas, on pourra alors écrire
ce qui résout l'équation différentielle.
La question est: dans quel cadre ce calcul a-t-il un sens ?
Un cadre possible est donné par les algèbres de convolution.
EXEMPLE 5.15 Les sous-espaces de
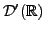
suivants sont des algèbres de convolution:
- L'espace
des distributions à support compact.
- L'espace des distributions à support limité à gauche.
- L'espace des distributions à support limité à droite.
- L'espace
des distributions à support dans
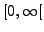 .
.
- L'espace
des distributions à support dans
.
Considérons l'équation de convolution
Etant donnée une algèbre de convolution
, et une distribution
, si il existe
telle que
alors il est possible de montrer que 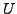 est unique dans
.
est unique dans
.
EXEMPLE 5.16 Dans
, soit
la distribution de Heaviside
(distribution régulière associée à la fonction de Heaviside).
On considère l'équation
On a déjà vu que
, et comme
,
on a
est l'inverse de convolution de
, et est donc la solution
élémentaire dans
de l'équation ci-dessus.
EXEMPLE 5.17 La primitive peut aussi s'interpréter en termes de solution fondamentale.
On considère cette fois l'équation, toujours dans
Comme on vient de le voir, l'inverse de convolution de
est
, qui est donc solution fondamentale de l'équation
ci-dessus.
On vient de voir que la dérivation des distributions est équivalente
à la convolution avec une dérivée de la distribution de Dirac. Un domaine
d'applications immédiat est constitué par les équations différentielles.
On se limite ici à un cadre relativement simple, qui permet toutefois de
cerner les points importants.
Considérons l'équation différentielle au sens des distributions
où les 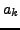 sont des coefficients fixés, et le membre de droite
est lui aussi fixé.
Comme on l'a vu, cette équation se met sous la forme
sont des coefficients fixés, et le membre de droite
est lui aussi fixé.
Comme on l'a vu, cette équation se met sous la forme
où la distribution
est donnée par
EXEMPLE 5.18 Considérons l'exemple simple d'un circuit
; on note
la
tension générée par un générateur, et
la tension aux bornes du
condensateur. Comme on l'a vu,
et
sont liés par
l'équation
où
. Il s'agit donc d'un problème de la forme
avec
,
et
.
La solution élémentaire prend donc la forme d'une distribution
régulière
où
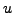
, solution de
avec
est donné par
Finalement, la solution est donc
La solution élémentaire possède une interprétation
physique simple: elle donne la réponse du système à une
``impulsion élémentaire'', représentée par une distribution de Dirac:
C'est pourquoi on appelle parfois
réponse impulsionnelle
la solution élémentaire.
Dans le cas où le système étudié (ici le circuit
)
est excité par une distribution
plus complexe, la solution
apparaît comme une superposition de ces réponses impulsionnelle.
Supposons maintenant que
soit une distribution régulière,
pour une certaine fonction
. On a alors
La fonction
prend la forme
Bruno Torresani
2007-06-26
![]() , est mesurée à l'aide d'un
dispositif expérimental. Ce dernier est généralement
incapable de reproduire les fluctuations les plus rapides de
, est mesurée à l'aide d'un
dispositif expérimental. Ce dernier est généralement
incapable de reproduire les fluctuations les plus rapides de
![]() , et ne donne pour approximation de la valeur
en
, et ne donne pour approximation de la valeur
en ![]() qu'une moyenne locale des valeurs de
qu'une moyenne locale des valeurs de ![]() dans un voisinage
de
dans un voisinage
de ![]() . On représente ceci via un produit de convolution
comme en (
. On représente ceci via un produit de convolution
comme en (![[*]](crossref.png) ), où la fonction
), où la fonction ![]() est une fonction localisée autour de 0
(de sorte que
est localisée autour de
), qui représente en
quelque sorte la réponse du dispositif expérimental.
est une fonction localisée autour de 0
(de sorte que
est localisée autour de
), qui représente en
quelque sorte la réponse du dispositif expérimental.
![]() , de la forme
, de la forme