Subsections
La notion de convergence d'une suite de nombres est une notion classique.
Par contre, dès lors que l'on s'intéresse à des suites de fonctions,
il est possible de donner à la notion de convergence de suites des sens
différents, qui traduisent des notions plus ou moins précises (ou fines)
de convergence.
On résume ici rapidement les notions de convergence les plus
usuelles, dans le cas de fonctions d'une variable réelle. Le cas des
fonctions de plusieurs variables s'en déduit sans difficulté.
On dit que la suite de fonctions
définies
sur un domaine 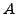 (soit donc
) converge
simplement vers la fonction
(soit donc
) converge
simplement vers la fonction 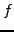 si pour tout
si pour tout 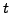 , la suite des
nombres
converge vers le nombre
.
On traduit cela par:
, la suite des
nombres
converge vers le nombre
.
On traduit cela par:
Cette notion de convergence n'est pas la notion la plus fine, dans la
mesure où le nombre
peut ici dépendre du point 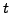 considéré. Lorsque cet aspect n'est pas souhaitable, on préfère
utiliser la notion de convergence uniforme.
considéré. Lorsque cet aspect n'est pas souhaitable, on préfère
utiliser la notion de convergence uniforme.
La contrainte de convergence uniforme est donc plus exigeante, et
suppose que l'on puisse contrôler l'erreur commise en approximant
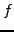 par
par 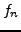 de façon indépendante du point étudié.
de façon indépendante du point étudié.
Bien évidemment, la convergence uniforme entraîne la convergence simple.
Les deux notions de convergence ci-dessus sont basées sur les
valeurs ponctuelles des fonctions étudiées. Or, il est souvent utile
de s'abstraire de l'utilisation des valeurs ponctuelles, et de définir
des notions de convergence en moyenne.
Soit 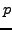 un nombre réel positif.
On dit que la suite de fonctions
définies
sur un domaine
un nombre réel positif.
On dit que la suite de fonctions
définies
sur un domaine 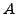 (soit donc
) converge
vers
(soit donc
) converge
vers 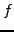 en moyenne d'ordre
en moyenne d'ordre 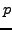 si la suite
tend vers zéro lorsque
si la suite
tend vers zéro lorsque 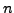 tend vers l'infini:
tend vers l'infini:
Pour que ces notions aient un sens, il faut bien entendu que les
intégrales
existent pour tout 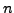 . Ceci
est assuré dès que l'on se place dans le cadre des
espaces de Lebesgue appropriés, c'est à dire si l'on
suppose que
. Les espaces
sont définis dans
l'Annexe
. Ceci
est assuré dès que l'on se place dans le cadre des
espaces de Lebesgue appropriés, c'est à dire si l'on
suppose que
. Les espaces
sont définis dans
l'Annexe ![[*]](crossref.png) .
.
La convergence en moyenne d'ordre 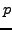 n'implique nullement la
convergence uniforme ni la convergence simple. On en verra des
contre exemples dans l'étude des séries de Fourier.
Par contre, la convergence en moyenne d'ordre
n'implique nullement la
convergence uniforme ni la convergence simple. On en verra des
contre exemples dans l'étude des séries de Fourier.
Par contre, la convergence en moyenne d'ordre 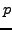 entraîne
la convergence simple presque partout.
entraîne
la convergence simple presque partout.
On dit que la suite de fonctions
définies
sur un domaine 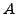 (soit donc
) converge presque partout
vers
(soit donc
) converge presque partout
vers 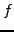 si pour tout
,
, à l'exception
éventuellement d'un ensemble de mesure nulle.
si pour tout
,
, à l'exception
éventuellement d'un ensemble de mesure nulle.
Bruno Torresani
2007-06-26
![]() un nombre réel positif.
On dit que la suite de fonctions
définies
sur un domaine
un nombre réel positif.
On dit que la suite de fonctions
définies
sur un domaine ![]() (soit donc
) converge
vers
(soit donc
) converge
vers ![]() en moyenne d'ordre
en moyenne d'ordre ![]() si la suite
tend vers zéro lorsque
si la suite
tend vers zéro lorsque ![]() tend vers l'infini:
tend vers l'infini:
![[*]](crossref.png) .
.
![]() n'implique nullement la
convergence uniforme ni la convergence simple. On en verra des
contre exemples dans l'étude des séries de Fourier.
Par contre, la convergence en moyenne d'ordre
n'implique nullement la
convergence uniforme ni la convergence simple. On en verra des
contre exemples dans l'étude des séries de Fourier.
Par contre, la convergence en moyenne d'ordre ![]() entraîne
la convergence simple presque partout.
entraîne
la convergence simple presque partout.