Ces considérations nous permettent maintenant de nous pencher sur
des espaces caractérisant les propriétés d'intégrabilité
des fonctions, aprés avoir examiné des espaces caractérisant
leurs propriétés de régularité.
A partir de maintenant, 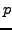 désigne un nombre réel supérieur à 1:
. A toute fonction
désigne un nombre réel supérieur à 1:
. A toute fonction  , on associe le nombre
, on associe le nombre
Ceci permet d'introduire les espaces de Lebesgue
Il est important de remarquer que l'intégrale utilisée ici étant
l'intégrale de Lebesgue, les fonctions de
doivent être
vues plutôt comme des classes d'équivalence de fonctions
(deux fonctions étant équivalentes si elles diffèrent sur un ensemble
de mesure nulle) que comme des fonctions définies en chaque point.
Ceci étant entendu, l'application
définit une
norme sur
:
- Inégalité triangulaire:
si
,
.
- si
et
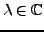 ,
.
,
.
-
implique
.
REMARQUE B..2 Il n'est pas tout à fait exact de dire que l'application
définit une norme sur les espaces
ainsi définis. En effet, si
presque partout, alors
,
sans que

soit nécessairement uniformément nulle. Pour s'abstraire
de ce problème, on convient d'identifier les fonctions qui ne diffèrent
que sur un ensemble de mesure nulle. Dans ce cas, la propriété
3 ci dessus est bien vérifiée.
REMARQUE B..3 Les normes introduites plus haut permettent de proposer de nouveaux critères
de convergence pour les suites de fonction. On dira par exemple que la suite
de fonctions de
converge vers une
fonction
en moyenne d'ordre
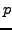
si
. La vérification de la convergence
en moyenne d'ordre
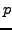
utilise souvent le théorème de convergence
dominée que nous avons vu plus haut.
Parmi les espaces
, l'espace
possède un statut particulier:
il possède un produit scalaire: si
, on définit
Ce produit scalaire est associé à la norme
, par
On montre que ce produit est sesquilinéaire, c'est à dire qu'il
vérifie les conditions suivantes:
- Hermiticité: si
, on a
.
- Linéarité à droite:
pour tous
,
.
- Positivité: soit
. Si pour toute
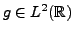 , on a
, alors
.
, on a
, alors
.
En conséquence des propriétés précédentes, nous avons donc
antilinéarité à gauche:
pour tous
,
.
Les espaces de Lebesgue possèdent des propriétés intéressantes
et utiles, appelées inégalités de Hölder et
inégalités d'Young, qui sont des généralisations
de l'inégalité de Cauchy-Schwarz.
Nous les donnons sans démonstration ci-dessous.
REMARQUE B..4 On vérifie bien que dans le cas
, on a
, et donc
l'inégalité de Hölder correspondante se ramène bien à
l'inégalité de Cauchy-Schwarz.
Bruno Torresani
2007-06-26
![]() désigne un nombre réel supérieur à 1:
. A toute fonction
désigne un nombre réel supérieur à 1:
. A toute fonction ![]() , on associe le nombre
, on associe le nombre